What is the electric current? First recall, what is the definition of current we have learned?

Quite simply, the directional movement of charged particles in a conductor is an electric current.

Only when a substance has charged particles that can move freely, it can transmit electric current—that is, conduct electricity. These charged particles that participate in conduction are called carriers. For metals, for example, only the outer electrons of atoms can act as carriers.

The “directional movement” in the definition of electric current is often misunderstood. Many people think it refers to movement with a certain direction, of course not! Doesn’t the direction of movement of the electrons in the AC circuit change?

In fact, orienteering is relative to “random movement”!

Since electrons are microscopic particles, they must be in thermal motion all the time. Thermal motion is a random motion, as shown in the figure below.

This movement is actually very fast. For example, in metals at room temperature, the speed of electronic thermal movement is on the order of hundreds of kilometers per second!

If you look closely at this random movement, you will find that the direction of movement of each particle is random at any moment. If you add up the velocity vectors of these particles, the result is almost zero.

Now add an electric field to the conductor, and the electron superimposes a directional movement on the basis of random movement. Assuming that the electric field is to the left for a certain period of time, the movement of the electrons looks like the following. The red balls represent metal atoms on the crystal lattice, and the fast moving dots represent free electrons.

Does it look fast? That’s because electronic movement is really fast! But in fact, the random motion, which accounts for a large proportion of it, does not contribute to the current. When the random motion is eliminated, the rest is just like the slow look below.

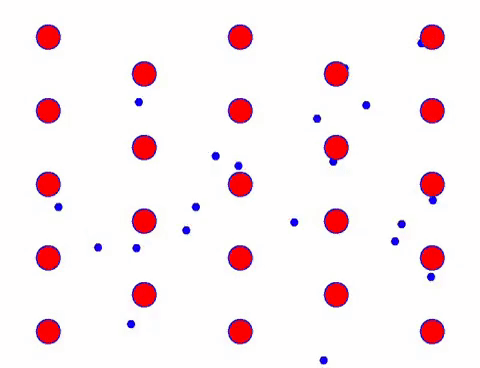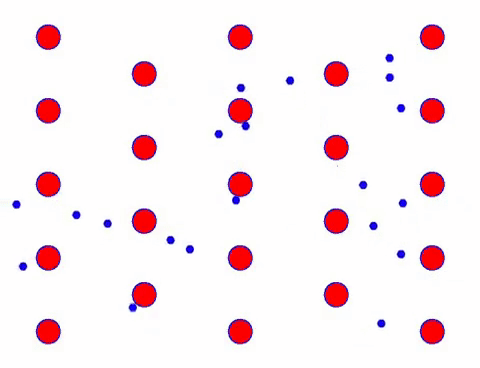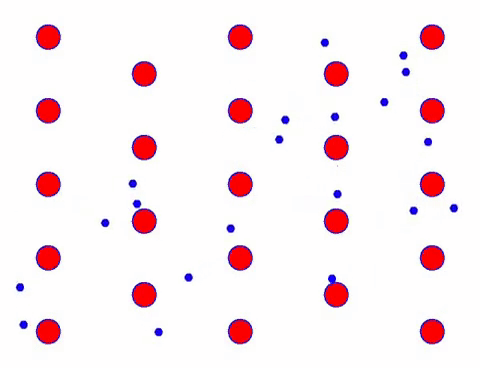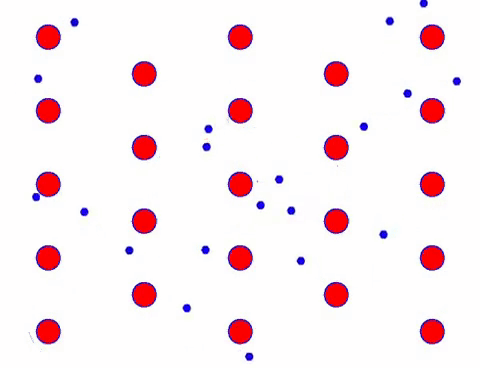
Indeed, the directional movement of electrons is much slower than the speed of thermal movement. This “grinding” movement of electrons is called drift, or “drift”. Sometimes, electrons will run in the opposite direction because of collisions with atoms. But in general, electrons move in one direction.

If the electric field changes direction, the direction of electron drift will also change.

Therefore, this kind of directional movement means that the sum of the speeds of all the electrons participating in the conduction at a certain time is not zero, but is generally in a certain direction. This direction can be changed at any time, and that is the case of alternating current.

Therefore, current is not so much the “directional movement” of electric charge as it is the “collective movement” of electric charge.

The magnitude of the current in the conductor is expressed by the current intensity. The current intensity is defined as the amount of electricity passing through the cross-section of the conductor in a unit time, namely

We have learned some physical quantities that contain the word “intensity”, such as electric field intensity and magnetic induction intensity. They generally represent the apportionment per unit time, unit area (or unit volume, unit solid angle). However, the word “intensity” in the current intensity does not reflect the current apportionment of the area.

In fact, another physical quantity is responsible for the distribution of current to area, which is current density.

Since the essence of electric current is the directional movement of electric charge, there must be a certain relationship between current intensity and drift speed!

In order to obtain this relationship, we must first clarify a concept-carrier concentration, that is, the number of carriers in a unit volume, which is expressed by .

It is assumed that the conductor cross section is, the carrier concentration is, the drift velocity is, and the charged charge is.

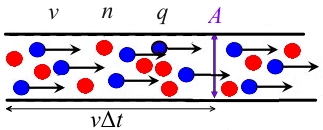
Then the charge in the conductor on the left side of the surface is, and these charges will pass through the surface within a certain period of time, so

This is a microscopic expression of current intensity.

Current density is the apportionment of current to area, so the magnitude of current density is, but it is defined as a vector, and the direction is the direction of the drift velocity vector of the positively charged carriers, so the drift of electrons in the metal can be obtained from this Speed, as an example below.

Consider a copper wire, assuming that each copper atom contributes an electron as a carrier. There is 1 mol of copper, its volume is, molar mass is, density is, then the carrier concentration of the copper wire is

Where is Avogadro’s constant. The density of copper is found, and the value obtained by substituting is about unit/cubic meter.

Assuming that the radius of the copper wire is 0.8mm, the current flowing is 15A, =1.6 C, and the drift velocity of electrons is calculated as

It can be seen that the drift speed of electrons is indeed very small.

For those who study circuits, the above is the complete definition of current.

But in physics, the above definition of current is actually only a narrow definition. More general currents are not limited to conductors, as long as the movement of electric charges is current. For example, when the electrons of a hydrogen atom move around the nucleus, an electric current is formed in its orbit.

Suppose the amount of electronic charge is and the period of movement is. Then every time that elapses, there is such a large amount of charge passing through any cross section of the loop, so the current intensity is based on the relationship between period, frequency and angular velocity, and the current can also be expressed as

For another example, a charged metal disk, rotating around its axis, also forms loop currents with different radii.

This kind of current is not a normal conduction current and cannot generate Joule heat! Can not form a real circuit.

Otherwise, would you give me a calculation of how much joule heat is generated per second by the electrons of the hydrogen atom?

In fact, the current in vacuum does not satisfy Ohm’s law. Because, for the electric current formed by the movement of charged particles in the vacuum, the carriers are not collided similar to the lattice in the metal, so the vacuum has no resistance and no conductance.

The movement of electric charges generates electric current, and the electric charge itself excites the electric field. This is easy to cause a misunderstanding. Many people therefore think that the electric field of the charged particles that form the electric current must be exposed. But in fact, for the conduction current in a general conductor, carriers flow on a background composed of a large number of positively charged metal ions, and the conductor itself is neutral!

We often call this kind of special current an “equivalent current”. The equivalent here means that it generates a magnetic field on the same basis as an ordinary conduction current!

Reminder: Do not confuse the “equivalent current” here with the “equivalent circuit” in circuit analysis

In fact, when we first studied the magnetic field, the electric current in Biot-Saffar’s law was the generalized electric current that contained this equivalent current. Of course, the conduction current in Maxwell’s equations also refers to the generalized current.

Those who have studied the photoelectric effect know that when the photoelectron drifts from the cathode to the anode, if the influence of air is ignored, this current is caused by the movement of electric charges in the vacuum, and there is no resistance, so it is not restricted by Ohm’s law.

So, is this the only thing about electric current in physics?

No! There are also two types, namely magnetizing current and displacement current.

They are also two equivalent currents, which, as the name suggests, are also introduced to explain magnetism. In other words, they have broken away from the basic characteristic of the current “charge movement”!

That’s amazing! There is no electric charge movement, so why can it be called an electric current?

Don’t worry, and listen to me slowly.

Let’s look at the magnetizing current first.

It was found that magnetism is caused by the movement of electricity (not considering the explanation of magnetism by the intrinsic properties of spin for the time being). In order to explain natural magnetism, French physicist Ampere put forward the hypothesis of “molecular circulation”.

As shown in the figure below, any atom or molecule can be regarded as having an electric charge rotating around the center, forming a tiny loop current, that is, “molecular circulation”.

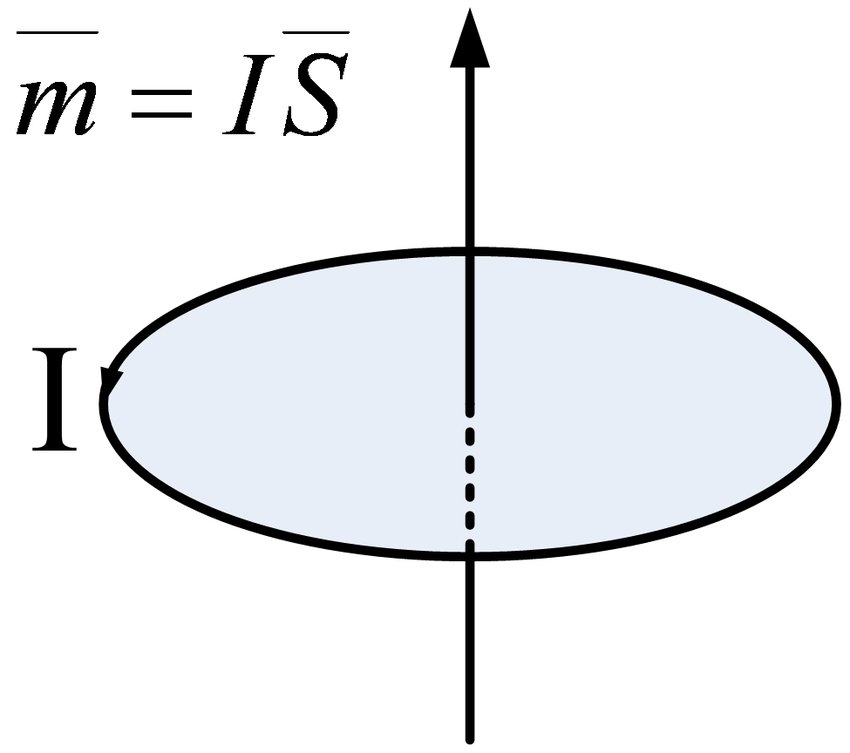
According to the law that the electric current excites the magnetic field, this molecular circulation will produce a physical quantity called magnetic moment. Its size is the area enclosed by the molecular circulation multiplied by the equivalent current of the molecular circulation, and its direction is in a right-handed spiral relationship with the direction of the circulation, namely

Obviously, the direction of the magnetic moment is exactly along the direction of the magnetic field formed by the circulating current

.

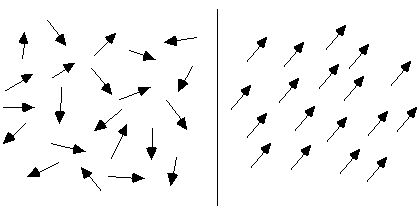
Under normal circumstances, the arrangement of the molecular circulation of a substance is chaotic, so the substance is not magnetic, as shown on the left side of the figure below. When subjected to an external magnetic field, these molecular circulations will be approximately neatly arranged. As shown on the right side of the figure below, their magnetic moments are arranged in one direction as much as possible, just like countless small magnetic needles gathered together to form a total magnetic field, and the whole material composed of them becomes magnetic.

Suppose there is a cylindrical magnet, the inner molecular circulation is neatly arranged, and the sections of each molecular circulation at the edge of the magnet section are connected together to form a large circulation, as shown in the figure below.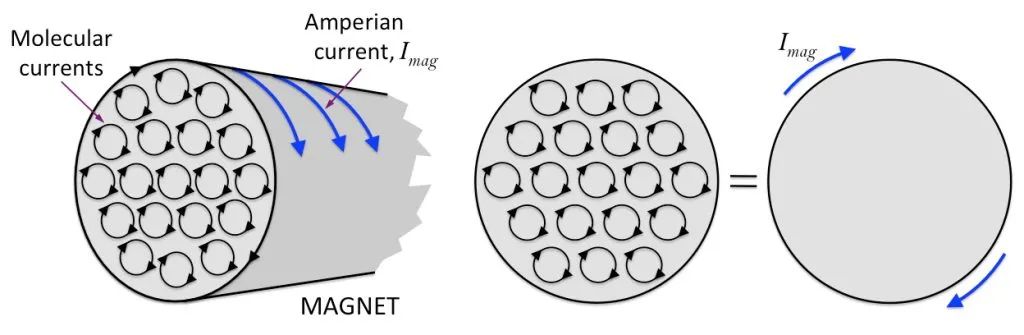

Based on this, we can think that a bar magnet is like an energized solenoid. In other words, there is an invisible current entangled on the surface of the magnet! This kind of current cannot be connected and used. It is confined to the surface of the magnet. We call it “binding current” or “magnetizing current”.

Therefore, the magnetizing current is a current, because it is the same as the current formed by the movement of real electric charges, which can equivalently generate a magnetic field!

Let’s look at the displacement current again.

According to the Ampere’s loop theorem, the integral of the magnetic field strength on a closed path is equal to the flux of the current density on any curved surface bounded by this path, that is, this theorem is called Stokes’ theorem in mathematics. It tells us that the integral of a vector along any closed path must be equal to the flux of its curl (here) to any surface bounded by the closed path.

Since it is a mathematical theorem, it must always be correct, because mathematics is a logical system based on axioms.

Therefore, the Ampere Loop Theorem must always hold!

However, the talented Scottish physicist Maxwell discovered that when faced with an unstable current circuit, the Ampere loop theorem was contradictory.

The typical unstable current occurs during the charging and discharging of the capacitor. As shown in the figure below, there is an unstable current during the short period of capacitor charging.

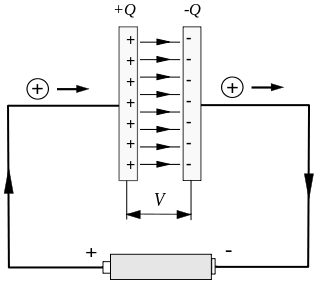
But the circuit is disconnected between the capacitor plates, which will cause a serious problem.

Suppose we consider a closed path that bypasses the wire, as shown in the figure below, the circle marked by C, and the curved surface with it as the boundary can be arbitrarily selected. In the figure, the circular plane enclosed by C itself and across the capacitor are selected. The curved surface of the left plate.

According to the circular surface, it can be seen that according to the curved surface, but as a loop integral of the magnetic field strength, its value should be determined!

How to do?

Maxwell believes that the Ampere’s loop theorem must be established. Now that there is a problem, it must be because a part of the current has not been discovered by us before, but it does exist!

So, how to find out this part of the current?

Since the problem is between the plates, start from between the plates.

Through analysis, Maxwell found that regardless of charging or discharging, there is a physical quantity between the capacitor plates at all times that is synchronized with the magnitude and direction of the current. It is the time derivative of the flux of the electric displacement vector, that is, it is defined as the displacement current.

If it is considered that this part is the part of the current that has not been discovered before, then the complete current is now. That is to say, although the circuit between the plates is disconnected, the derivative of the electric displacement flux and the sum of the current together, as a whole , Ensure the continuity of the current at all times.

Going back to the previous contradiction, we now know that, according to the requirements of Stokes’ theorem, when calculating the flux of current density for a closed surface, the density of displacement current should also be considered, that is, the complete ampere loop theorem is therefore, By “discovering” this new current component, the crisis of the Ampere Loop Theorem is resolved!

The reason why “introduction” is not used here, but “discovery” is used here. What I want to emphasize is that this kind of current is not a mathematical compensation, but a real thing, but it has not been discovered before.

Why does it exist in the first place? Because it acts as an electric current, like a conduction current, it excites a magnetic field equivalently, except that there is no movement of electric charges, no wire is required, and no Joule heat can be generated, so it has been ignored!

But it actually exists by itself, just keep a low profile, it has been silently exciting the magnetic field there all the time!

In other words, when we face a magnetic field, the original definition of current is too narrow. The essence of electric current is not the movement of electric charge, it should be something that can excite a magnetic field.

So far, the several forms of current have been introduced. They all exist objectively, and what they have in common is that all currents can equally excite the magnetic field.