מהו הזרם החשמלי? זכרון ראשון, מהי ההגדרה של זרם שלמדנו?

פשוט למדי, התנועה הכיוונית של חלקיקים טעונים במוליך היא זרם חשמלי.

רק כאשר לחומר יש חלקיקים טעונים שיכולים לנוע בחופשיות, הוא יכול להעביר זרם חשמלי – כלומר להוליך חשמל. חלקיקים טעונים אלה המשתתפים בהולכה נקראים נשאים. עבור מתכות, למשל, רק האלקטרונים החיצוניים של אטומים יכולים לפעול כנשאים.

ה”תנועה הכיוונית” בהגדרה של זרם חשמלי מובנת לעתים קרובות לא נכון. אנשים רבים חושבים שזה מתייחס לתנועה עם כיוון מסוים, כמובן שלא! האם כיוון התנועה של האלקטרונים במעגל AC לא משתנה?

למעשה, התמצאות היא יחסית ל”תנועה אקראית”!

מכיוון שהאלקטרונים הם חלקיקים מיקרוסקופיים, הם חייבים להיות בתנועה תרמית כל הזמן. תנועה תרמית היא תנועה אקראית, כפי שמוצג באיור למטה.

התנועה הזו היא למעשה מהירה מאוד. לדוגמה, במתכות בטמפרטורת החדר, מהירות התנועה התרמית האלקטרונית היא בסדר גודל של מאות קילומטרים לשנייה!

אם תסתכלו מקרוב על התנועה האקראית הזו, תגלו שכיוון התנועה של כל חלקיק הוא אקראי בכל רגע. אם מחברים את וקטורי המהירות של החלקיקים הללו, התוצאה היא כמעט אפס.

כעת הוסף שדה חשמלי למוליך, והאלקטרון מציב תנועה כיוונית על בסיס תנועה אקראית. בהנחה שהשדה החשמלי נמצא משמאל לפרק זמן מסוים, תנועת האלקטרונים נראית כך. הכדורים האדומים מייצגים אטומי מתכת על סריג הגביש, והנקודות הנעות במהירות מייצגות אלקטרונים חופשיים.

זה נראה מהיר? זה בגלל שהתנועה האלקטרונית היא ממש מהירה! אך למעשה, התנועה האקראית, המהווה חלק גדול ממנה, אינה תורמת לזרם. כאשר התנועה האקראית מבוטלת, השאר הוא בדיוק כמו המראה האיטי למטה.

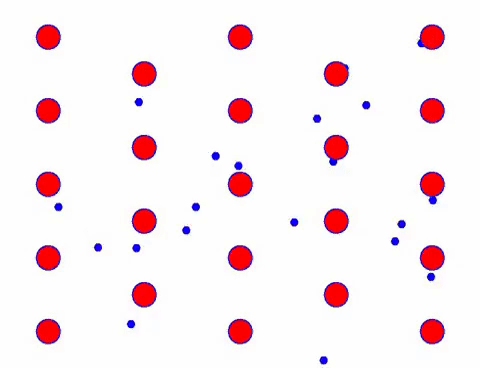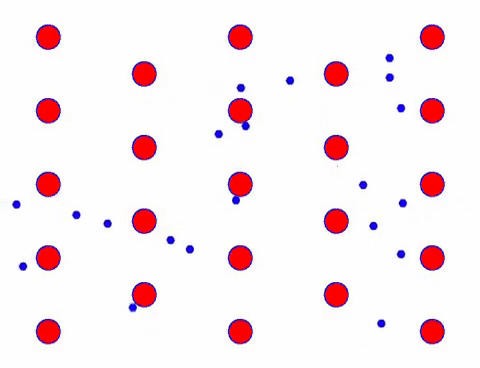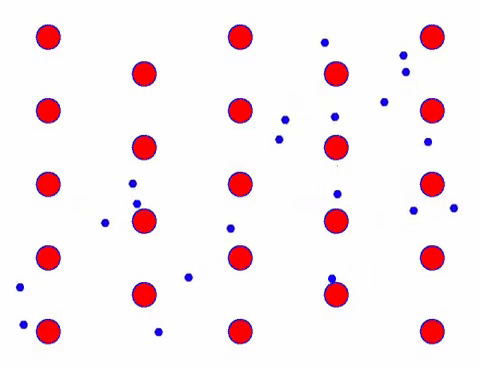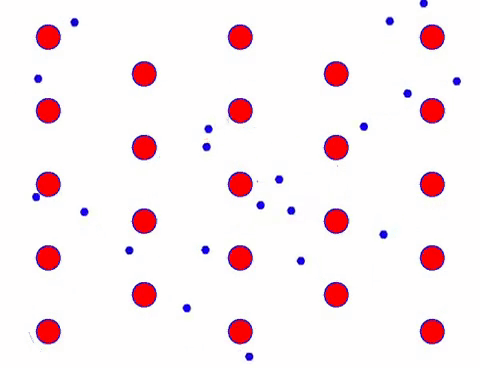
אכן, התנועה הכיוונית של אלקטרונים איטית בהרבה ממהירות התנועה התרמית. תנועת “טחינה” זו של אלקטרונים נקראת סחיפה, או “סחף”. לפעמים, אלקטרונים ירוצו בכיוון ההפוך בגלל התנגשויות עם אטומים. אבל באופן כללי, אלקטרונים נעים בכיוון אחד.

אם השדה החשמלי משנה כיוון, ישתנה גם כיוון סחיפת האלקטרונים.

לכן, תנועה כיוונית מסוג זה פירושה שסכום המהירויות של כל האלקטרונים המשתתפים בהולכה בזמן מסוים אינו אפס, אלא הוא בדרך כלל בכיוון מסוים. כיוון זה ניתן לשנות בכל עת, וזה המקרה של זרם חילופין.

לכן, זרם הוא לא כל כך “התנועה הכיוונית” של המטען החשמלי אלא “התנועה הקולקטיבית” של המטען החשמלי.

גודל הזרם במוליך מתבטא בעוצמת הזרם. עוצמת הזרם מוגדרת ככמות החשמל העוברת בחתך הרוחב של המוליך ביחידת זמן, כלומר

למדנו כמה כמויות פיזיקליות המכילות את המילה “עוצמה”, כמו עוצמת שדה חשמלי ועוצמת אינדוקציה מגנטית. הם בדרך כלל מייצגים את החלוקה ליחידת זמן, יחידת שטח (או יחידת נפח, יחידת זווית מוצקה). עם זאת, המילה “עוצמה” בעוצמה הנוכחית אינה משקפת את החלוקה הנוכחית של השטח.

למעשה, כמות פיזיקלית אחרת אחראית לחלוקת הזרם לאזור, שהיא צפיפות הזרם.

מכיוון שמהות הזרם החשמלי היא תנועה כיוונית של מטען חשמלי, חייב להיות קשר מסוים בין עוצמת הזרם למהירות הסחף!

על מנת לקבל קשר זה, עלינו להבהיר תחילה ריכוז מושג-נשא, כלומר מספר הנשאים בנפח יחידה, המתבטא ב-.

ההנחה היא שחתך המוליך הוא, ריכוז המוביל הוא, מהירות הסחף היא והמטען הטעון הוא.

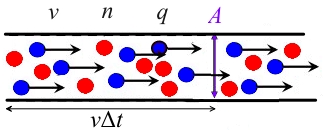
אז המטען במוליך בצד שמאל של המשטח הוא, והמטענים הללו יעברו דרך המשטח תוך פרק זמן מסוים, אז

זהו ביטוי מיקרוסקופי של עוצמת הזרם.

צפיפות זרם היא חלוקת הזרם לאזור, כך שגודל צפיפות הזרם הוא, אך הוא מוגדר כווקטור, והכיוון הוא כיוון וקטור מהירות הסחף של הנשאים הטעונים חיובית, כך שהסחיפה של אלקטרונים ב- ניתן להשיג מתכת מהמהירות הזו, כדוגמה למטה.

חשבו על חוט נחושת, בהנחה שכל אטום נחושת תורם אלקטרון כנשא. יש 1 מול נחושת, הנפח שלו הוא, המסה המולרית היא, הצפיפות היא, ואז ריכוז הנשא של חוט הנחושת הוא

איפה הקבוע של אבוגדרו. נמצאה צפיפות הנחושת, והערך המתקבל בהחלפה הוא כיחידה/מטר מעוקב.

בהנחה שרדיוס חוט הנחושת הוא 0.8 מ”מ, הזרם הזורם הוא 15A, =1.6 C, ומהירות הסחף של אלקטרונים מחושבת כ-

ניתן לראות שמהירות הסחף של אלקטרונים אכן קטנה מאוד.

למי שלומד מעגלים, האמור לעיל הוא ההגדרה המלאה של זרם.

אבל בפיזיקה, ההגדרה שלעיל של זרם היא למעשה רק הגדרה מצומצמת. זרמים כלליים יותר אינם מוגבלים למוליכים, כל עוד תנועת המטענים החשמליים היא זרם. לדוגמה, כאשר האלקטרונים של אטום מימן נעים סביב הגרעין, נוצר זרם חשמלי במסלולו.

נניח שכמות המטען האלקטרוני היא ותקופת התנועה היא. ואז בכל פעם שחולף, יש כמות כה גדולה של מטען שעוברת דרך כל חתך רוחב של הלולאה, כך שעוצמת הזרם מבוססת על הקשר בין תקופה, תדר ומהירות זוויתית, והזרם יכול להתבטא גם כ

לדוגמא אחרת, דיסק מתכת טעון, המסתובב סביב צירו, יוצרת גם זרמי לולאה עם רדיוסים שונים.

סוג זה של זרם אינו זרם הולכה רגיל ואינו יכול ליצור חום ג’ול! לא יכול ליצור מעגל אמיתי.

אחרת, האם תוכל לתת לי חישוב של כמה חום ג’אול נוצר בשנייה על ידי האלקטרונים של אטום המימן?

למעשה, הזרם בוואקום אינו עומד בחוק של אוהם. כי עבור הזרם החשמלי הנוצר מתנועת חלקיקים טעונים בוואקום, הנשאים אינם מתנגשים בדומה לסריג במתכת, ולכן לוואקום אין התנגדות ואין מוליכות.

תנועת המטענים החשמליים יוצרת זרם חשמלי, והמטען החשמלי עצמו מעורר את השדה החשמלי. זה קל לגרום לאי הבנה. לכן אנשים רבים חושבים שהשדה החשמלי של החלקיקים הטעונים היוצרים את הזרם החשמלי חייב להיות חשוף. אבל למעשה, עבור זרם ההולכה במוליך כללי, נשאים זורמים על רקע המורכב ממספר רב של יוני מתכת טעונים חיובית, והמוליך עצמו הוא ניטרלי!

לעתים קרובות אנו קוראים לסוג זה של זרם מיוחד “זרם שווה ערך”. המקבילה כאן פירושה שהוא יוצר שדה מגנטי על בסיס זהה לזרם הולכה רגיל!

תזכורת: אין לבלבל את “הזרם המקביל” כאן עם “המעגל המקביל” בניתוח מעגלים

למעשה, כאשר חקרנו לראשונה את השדה המגנטי, הזרם החשמלי בחוק ביו-ספאר היה הזרם החשמלי המוכלל שהכיל את הזרם המקביל הזה. כמובן, זרם ההולכה במשוואות מקסוול מתייחס גם לזרם המוכלל.

מי שחקר את האפקט הפוטואלקטרי יודע שכאשר הפוטואלקטרון נסחף מהקתודה לאנודה, אם מתעלמים מהשפעת האוויר, זרם זה נגרם מתנועת מטענים חשמליים בוואקום, ואין התנגדות, אז זה אינו מוגבל על ידי חוק אוהם.

אז, האם זה הדבר היחיד לגבי זרם חשמלי בפיזיקה?

לא! ישנם גם שני סוגים, כלומר זרם מגנט וזרם תזוזה.

הם גם שני זרמים שווים, שכפי שהשם מרמז, מוצגים גם כדי להסביר מגנטיות. במילים אחרות, הם נפרדו מהמאפיין הבסיסי של “תנועת המטען” הנוכחית!

זה מדהים! אין תנועת מטען חשמלי, אז למה אפשר לקרוא לזה זרם חשמלי?

אל תדאג, ותקשיב לי לאט.

בואו נסתכל תחילה על זרם הממגנט.

נמצא שמגנטיות נגרמת על ידי תנועת החשמל (בלי לקחת בחשבון את ההסבר של מגנטיות על ידי התכונות הפנימיות של ספין לעת עתה). על מנת להסביר את המגנטיות הטבעית, הפיזיקאי הצרפתי אמפר הציג את ההשערה של “מחזוריות מולקולרית”.

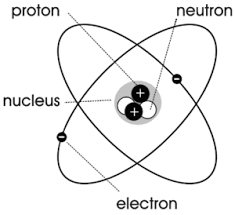
כפי שמוצג באיור למטה, ניתן להתייחס לכל אטום או מולקולה כבעל מטען חשמלי המסתובב סביב המרכז, ויוצר זרם לולאה זעיר, כלומר “מחזוריות מולקולרית”.

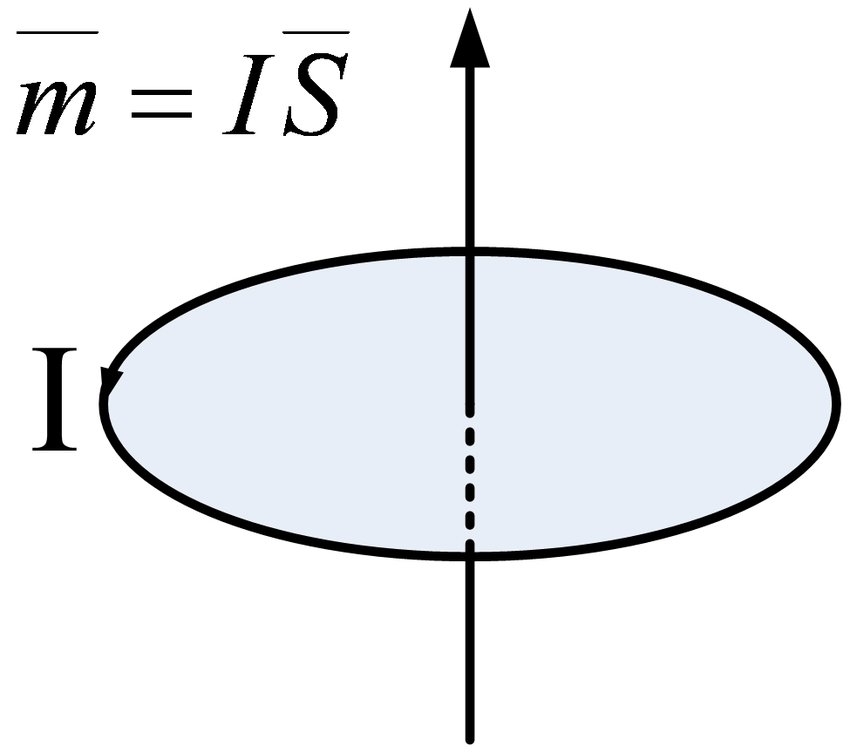
לפי החוק שהזרם החשמלי מעורר את השדה המגנטי, מחזוריות מולקולרית זו תייצר גודל פיזיקלי הנקרא מומנט מגנטי. גודלו הוא השטח המוקף על ידי המחזור המולקולרי כפול הזרם המקביל של המחזור המולקולרי, וכיוונו הוא ביחס ספירלי ימני עם כיוון המחזור, כלומר

ברור שכיוון המומנט המגנטי הוא בדיוק בכיוון השדה המגנטי שנוצר על ידי הזרם המסתובב

.

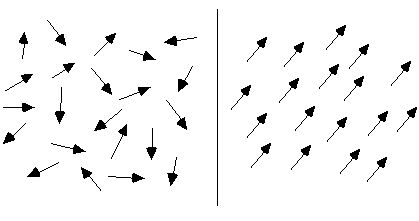
בנסיבות רגילות, סידור המחזור המולקולרי של חומר הוא כאוטי, ולכן החומר אינו מגנטי, כפי שמוצג בצד שמאל של האיור למטה. כאשר הם נתונים לשדה מגנטי חיצוני, מחזורי הדם המולקולריים האלה יהיו מסודרים בערך בצורה מסודרת. כפי שמוצג בצד ימין של האיור למטה, המומנטים המגנטיים שלהם מסודרים בכיוון אחד ככל האפשר, ממש כמו אינספור מחטים מגנטיות קטנות שנאספו יחד ליצירת שדה מגנטי כולל, וכל החומר המורכב מהם הופך למגנטי.

נניח שיש מגנט גלילי, המחזור המולקולרי הפנימי מסודר בצורה מסודרת, והקטעים של כל מחזוריות מולקולרית בקצה קטע המגנט מחוברים יחד ליצירת מחזור גדול, כפי שמוצג באיור למטה.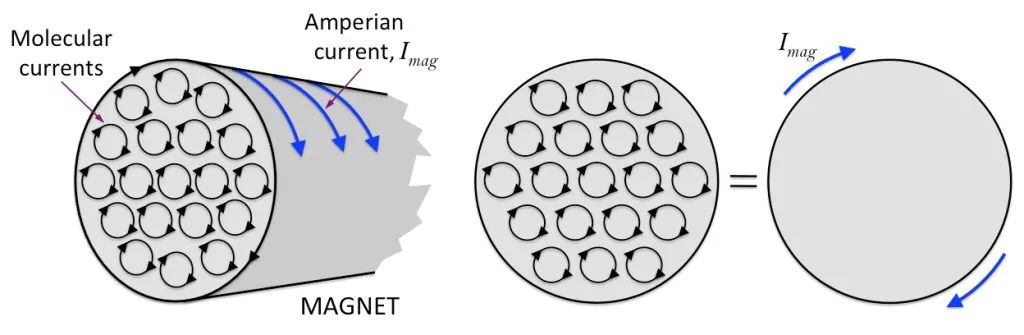

בהתבסס על זה, אנו יכולים לחשוב שמגנט מוט הוא כמו סולנואיד מופעל. במילים אחרות, יש זרם בלתי נראה מסתבך על פני המגנט! לא ניתן לחבר ולהשתמש בזרם מסוג זה. הוא מוגבל לפני השטח של המגנט. אנו קוראים לזה “זרם מחייב” או “זרם מגנט”.

לכן, הזרם הממגנט הוא זרם, מכיוון שהוא זהה לזרם הנוצר מתנועה של מטענים חשמליים אמיתיים, שיכולים ליצור באופן שווה שדה מגנטי!

בואו נסתכל שוב על זרם העקירה.

לפי משפט הלולאה של אמפר, האינטגרל של עוצמת השדה המגנטי בנתיב סגור שווה לשטף של צפיפות הזרם על כל משטח מעוקל התחום בנתיב זה, כלומר, משפט זה נקרא משפט סטוקס במתמטיקה. זה אומר לנו שהאינטגרל של וקטור לאורך כל נתיב סגור חייב להיות שווה לשטף התלתל שלו (כאן) לכל משטח התחום על ידי הנתיב הסגור.

מכיוון שזהו משפט מתמטי, הוא חייב להיות נכון תמיד, כי מתמטיקה היא מערכת לוגית המבוססת על אקסיומות.

לכן, משפט לולאת האמפר חייב להתקיים תמיד!

עם זאת, הפיזיקאי הסקוטי המוכשר מקסוול גילה שכאשר הוא מתמודד עם מעגל זרם לא יציב, משפט לולאת אמפר היה סותר.

הזרם הלא יציב האופייני מתרחש במהלך הטעינה והפריקה של הקבל. כפי שמוצג באיור למטה, יש זרם לא יציב במהלך התקופה הקצרה של טעינת הקבל.

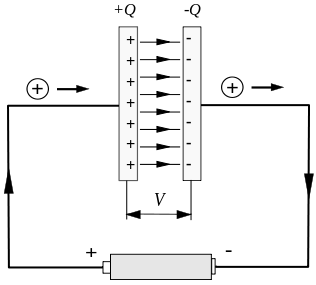
אבל המעגל מנותק בין לוחות הקבלים, מה שיגרום לבעיה רצינית.

נניח שאנו רואים נתיב סגור העוקף את החוט, כפי שמוצג באיור למטה, ניתן לבחור באופן שרירותי את המעגל המסומן ב-C ואת המשטח המעוגל איתו כגבול. באיור נבחר המישור העגול המוקף ב-C עצמו ולרוחב הקבל. המשטח המעוגל של הצלחת השמאלית.

לפי המשטח המעגלי, ניתן לראות שלפי המשטח המעוקל, אך כאינטגרל לולאה של עוצמת השדה המגנטי, יש לקבוע את ערכו!

איך לעשות?

מקסוול מאמין שיש לקבוע את משפט הלולאה של אמפר. עכשיו כשיש בעיה, זה בטח בגלל שחלק מהזרם לא התגלה על ידינו קודם, אבל הוא קיים!

אז איך לגלות את החלק הזה של הזרם?

מכיוון שהבעיה היא בין הצלחות, התחילו בין הצלחות.

באמצעות ניתוח, מקסוול מצא שללא קשר לטעינה או פריקה, ישנה כמות פיזית בין לוחות הקבלים בכל עת המסונכרנת עם גודל וכיוון הזרם. זוהי נגזרת הזמן של השטף של וקטור התזוזה החשמלי, כלומר, הוא מוגדר כזרם התזוזה.

אם נחשב שחלק זה הוא החלק של הזרם שלא התגלה קודם לכן, אז הזרם המלא הוא עכשיו. כלומר, למרות שהמעגל בין הלוחות מנותק, הנגזרת של שטף העקירה החשמלית וסכום הזרם ביחד, כמכלול, מבטיחות את המשכיות הזרם בכל עת.

אם נחזור לסתירה הקודמת, אנו יודעים כעת שלפי הדרישות של משפט סטוקס, כאשר מחשבים את שטף צפיפות הזרם עבור משטח סגור, יש להתייחס גם לצפיפות זרם העקירה, כלומר לולאת האמפר השלמה. לפיכך המשפט הוא, על ידי “גילוי” הרכיב הנוכחי החדש הזה, המשבר של משפט לולאת אמפר נפתר!

הסיבה לכך שלא משתמשים כאן ב”מבוא”, אלא ב”גילוי” כאן. מה שאני רוצה להדגיש הוא שזרם מסוג זה אינו פיצוי מתמטי, אלא דבר אמיתי, אך הוא לא התגלה בעבר.

למה זה קיים מלכתחילה? מכיוון שהוא פועל כזרם חשמלי, כמו זרם הולכה, הוא מעורר שדה מגנטי באופן שווה, אלא שאין תנועה של מטענים חשמליים, אין צורך בחוט, ולא ניתן ליצור חום ג’ול, ולכן התעלמו ממנו!

אבל זה בעצם קיים מעצמו, רק שמרו על פרופיל נמוך, הוא מרגש בשקט את השדה המגנטי שם כל הזמן!

במילים אחרות, כאשר אנו עומדים בפני שדה מגנטי, ההגדרה המקורית של זרם צרה מדי. המהות של זרם חשמלי היא לא תנועה של מטען חשמלי, זה צריך להיות משהו שיכול לעורר שדה מגנטי.

עד כה, הוצגו מספר צורות הזרם. כולם קיימים באופן אובייקטיבי, והמשותף להם הוא שכל הזרמים יכולים לעורר באותה מידה את השדה המגנטי.