전류는 무엇입니까? 먼저 우리가 배운 전류의 정의는 무엇입니까?

간단히 말해서, 도체에서 하전 입자의 방향성 운동은 전류입니다.

Only when a substance has charged particles that can move freely, it can transmit electric current—that is, conduct electricity. These charged particles that participate in conduction are called carriers. For metals, for example, only the outer electrons of atoms can act as carriers.

The “directional movement” in the definition of electric current is often misunderstood. Many people think it refers to movement with a certain direction, of course not! Doesn’t the direction of movement of the electrons in the AC circuit change?

사실 오리엔티어링은 ‘무작위 이동’과 관련이 있습니다!

Since electrons are microscopic particles, they must be in thermal motion all the time. Thermal motion is a random motion, as shown in the figure below.

이 움직임은 실제로 매우 빠릅니다. 예를 들어, 실온의 금속에서 전자 열 운동의 속도는 초당 수백 킬로미터입니다!

이 무작위적인 움직임을 자세히 보면 각 입자의 이동 방향이 임의의 순간에 있음을 알 수 있습니다. 이러한 입자의 속도 벡터를 더하면 결과는 거의 XNUMX입니다.

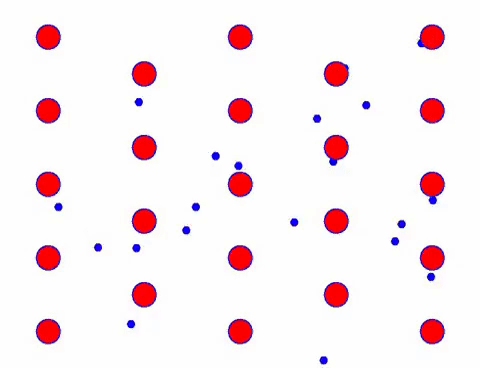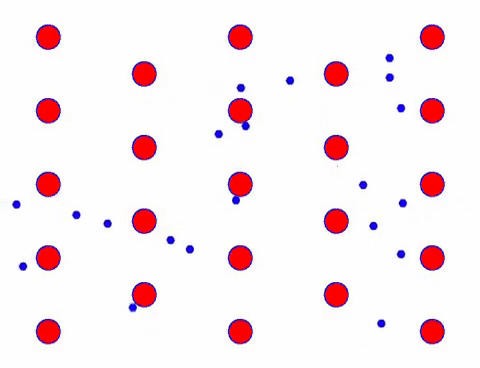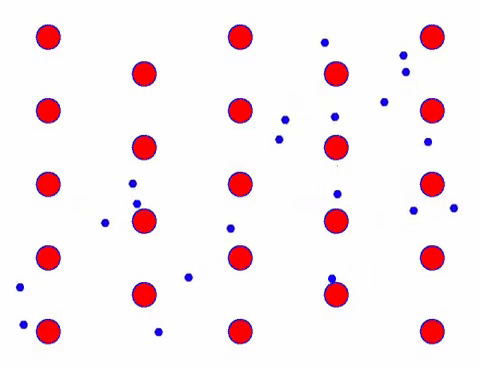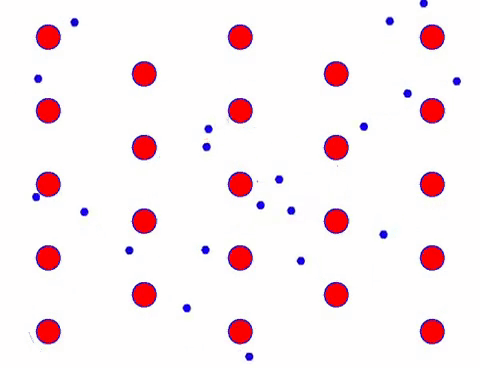
이제 도체에 전기장을 추가하면 전자가 무작위 이동을 기반으로 한 방향 이동을 중첩합니다. 일정 시간 동안 전기장이 왼쪽으로 있다고 가정하면 전자의 움직임은 다음과 같습니다. 빨간 공은 결정 격자의 금속 원자를 나타내고 빠르게 움직이는 점은 자유 전자를 나타냅니다.

Does it look fast? That’s because electronic movement is really fast! But in fact, the random motion, which accounts for a large proportion of it, does not contribute to the current. When the random motion is eliminated, the rest is just like the slow look below.

실제로 전자의 방향 이동은 열 이동 속도보다 훨씬 느립니다. 이러한 전자의 “갈기” 움직임을 드리프트 또는 “드리프트”라고 합니다. 때때로 전자는 원자와의 충돌로 인해 반대 방향으로 움직입니다. 그러나 일반적으로 전자는 한 방향으로 움직입니다.

전기장의 방향이 바뀌면 전자 드리프트의 방향도 바뀝니다.

따라서 이러한 종류의 방향성 이동은 특정 시간에 전도에 참여하는 모든 전자의 속도의 합이 XNUMX이 아니라 일반적으로 특정 방향을 의미함을 의미한다. 이 방향은 언제든지 변경할 수 있으며 이것이 교류의 경우입니다.

따라서 전류는 전하의 “방향성 이동”이 아니라 전하의 “집합적 이동”입니다.

도체에 흐르는 전류의 크기는 전류 강도로 표시됩니다. 전류 강도는 단위 시간 동안 도체의 단면을 통과하는 전기의 양으로 정의됩니다.

We have learned some physical quantities that contain the word “intensity”, such as electric field intensity and magnetic induction intensity. They generally represent the apportionment per unit time, unit area (or unit volume, unit solid angle). However, the word “intensity” in the current intensity does not reflect the current apportionment of the area.

In fact, another physical quantity is responsible for the distribution of current to area, which is current density.

전류의 본질은 전하의 방향성 운동이기 때문에 전류 강도와 드리프트 속도 사이에는 일정한 관계가 있어야 합니다!

이 관계를 얻기 위해서는 먼저 개념-운반체 농도, 즉 로 표시되는 단위 부피의 담체 수를 명확히 해야 합니다.

It is assumed that the conductor cross section is, the carrier concentration is, the drift velocity is, and the charged charge is.

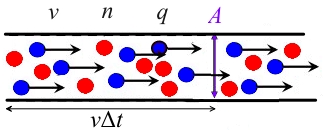
그러면 표면 왼쪽에 있는 도체의 전하가 이고 이 전하들은 일정 시간 동안 표면을 통과하므로

This is a microscopic expression of current intensity.

전류밀도는 면적에 대한 전류의 배분이므로 전류밀도의 크기는 이지만 벡터로 정의되고 방향은 양전하를 띤 캐리어의 드리프트 속도 벡터의 방향이므로 전자의 드리프트는 금속은 아래 예와 같이 이 속도에서 얻을 수 있습니다.

Consider a copper wire, assuming that each copper atom contributes an electron as a carrier. There is 1 mol of copper, its volume is, molar mass is, density is, then the carrier concentration of the copper wire is

Avogadro의 상수는 어디에 있습니까? 구리의 밀도를 구하고 대입한 값은 대략 단위/세제곱미터이다.

Assuming that the radius of the copper wire is 0.8mm, the current flowing is 15A, =1.6 C, and the drift velocity of electrons is calculated as

It can be seen that the drift speed of electrons is indeed very small.

For those who study circuits, the above is the complete definition of current.

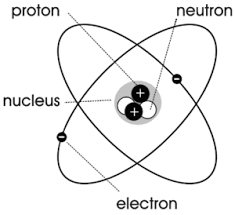
But in physics, the above definition of current is actually only a narrow definition. More general currents are not limited to conductors, as long as the movement of electric charges is current. For example, when the electrons of a hydrogen atom move around the nucleus, an electric current is formed in its orbit.

전자 전하량은 이고 이동 주기는 이라고 하자. 그런 다음 경과 할 때마다 루프의 모든 단면을 통과하는 많은 양의 전하가 있으므로 전류 강도는 주기, 주파수 및 각속도 간의 관계를 기반으로 하며 전류는 다음과 같이 나타낼 수도 있습니다.

또 다른 예를 들어, 축을 중심으로 회전하는 충전된 금속 디스크도 반지름이 다른 루프 전류를 형성합니다.

이러한 종류의 전류는 정상적인 전도 전류가 아니며 줄 열을 생성할 수 없습니다! 실제 회로를 형성할 수 없습니다.

그렇지 않으면 수소 원자의 전자가 초당 얼마나 많은 줄 열을 생성하는지 계산해 주시겠습니까?

사실, 진공의 전류는 옴의 법칙을 만족하지 않습니다. 진공 상태에서 하전 입자의 이동에 의해 형성된 전류의 경우 금속의 격자와 같이 캐리어가 충돌하지 않으므로 진공에는 저항과 컨덕턴스가 없습니다.

전하의 이동은 전류를 생성하고 전하 자체가 전기장을 여기시킨다. 이것은 오해를 일으키기 쉽습니다. 따라서 많은 사람들은 전류를 형성하는 하전 입자의 전기장이 노출되어야 한다고 생각합니다. 그러나 사실 일반도체의 도통전류는 양전하를 띤 다수의 금속이온으로 구성된 배경에 캐리어가 흐르고 도체 자체는 중성이다!

We often call this kind of special current an “equivalent current”. The equivalent here means that it generates a magnetic field on the same basis as an ordinary conduction current!

Reminder: Do not confuse the “equivalent current” here with the “equivalent circuit” in circuit analysis

사실, 우리가 자기장을 처음 연구했을 때 Biot-Saffar의 법칙에서 전류는 이 등가 전류를 포함하는 일반화된 전류였습니다. 물론 맥스웰 방정식의 전도전류도 일반화된 전류를 의미한다.

Those who have studied the photoelectric effect know that when the photoelectron drifts from the cathode to the anode, if the influence of air is ignored, this current is caused by the movement of electric charges in the vacuum, and there is no resistance, so it is not restricted by Ohm’s law.

So, is this the only thing about electric current in physics?

아니요! 또한 자화 전류와 변위 전류의 두 가지 유형이 있습니다.

그들은 또한 이름에서 알 수 있듯이 자기를 설명하기 위해 도입된 두 개의 등가 전류입니다. 즉, 그들은 현재의 “충전 운동”의 기본 특성에서 이탈했습니다!

That’s amazing! There is no electric charge movement, so why can it be called an electric current?

걱정하지 말고 천천히 내 말을 들어라.

Let’s look at the magnetizing current first.

자성은 전기의 이동에 의해 발생한다는 것을 알아냈습니다(당분간 스핀의 고유한 성질에 의한 자성의 설명은 고려하지 않음). 자연 자기를 설명하기 위해 프랑스 물리학자 암페어는 “분자 순환” 가설을 제시했습니다.

아래 그림과 같이 모든 원자나 분자는 전하가 중심을 중심으로 회전하여 작은 루프 전류, 즉 “분자 순환”을 형성하는 것으로 간주할 수 있습니다.

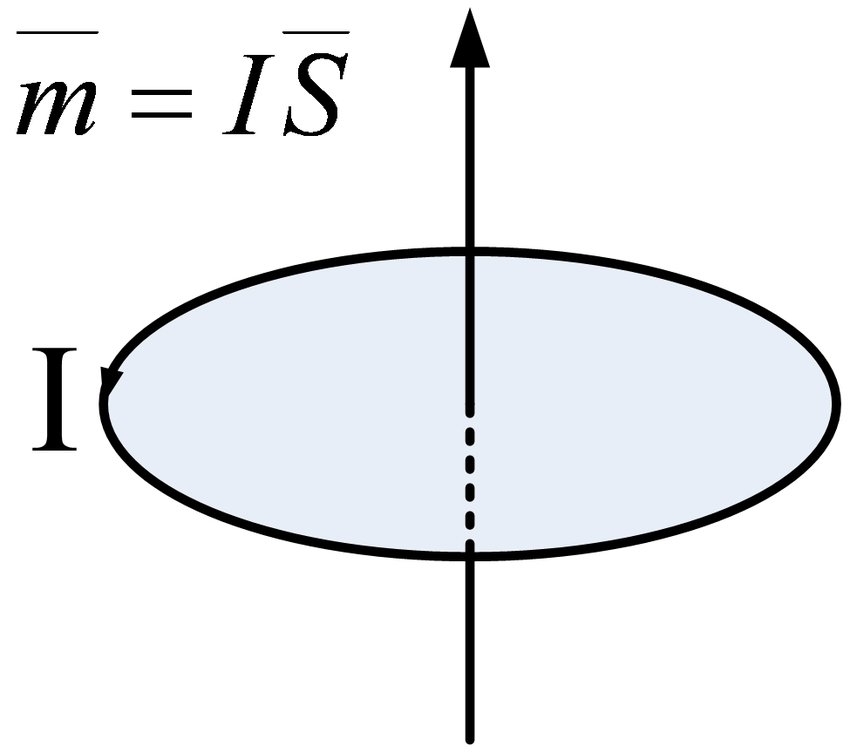
According to the law that the electric current excites the magnetic field, this molecular circulation will produce a physical quantity called magnetic moment. Its size is the area enclosed by the molecular circulation multiplied by the equivalent current of the molecular circulation, and its direction is in a right-handed spiral relationship with the direction of the circulation, namely

Obviously, the direction of the magnetic moment is exactly along the direction of the magnetic field formed by the circulating current

.

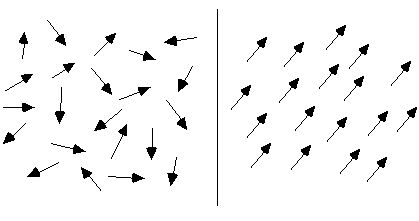
정상적인 상황에서 물질의 분자 순환 배열은 무질서하므로 물질은 아래 그림의 왼쪽과 같이 자성이 없습니다. 외부 자기장을 받으면 이러한 분자 순환이 대략 깔끔하게 배열됩니다. 아래 그림의 오른쪽과 같이 무수한 작은 자침이 모여 전체 자기장을 형성하는 것과 같이 자기 모멘트가 최대한 한 방향으로 배열되어 전체 자기장을 형성하게 되며, 이를 구성하는 물질 전체가 자기가 됩니다.

아래 그림과 같이 원통형 자석이 있고 내부의 분자순환이 가지런히 배열되어 있고 자석 부분의 가장자리에 있는 각 분자순환의 단면이 서로 연결되어 큰 순환을 이룬다고 가정하자.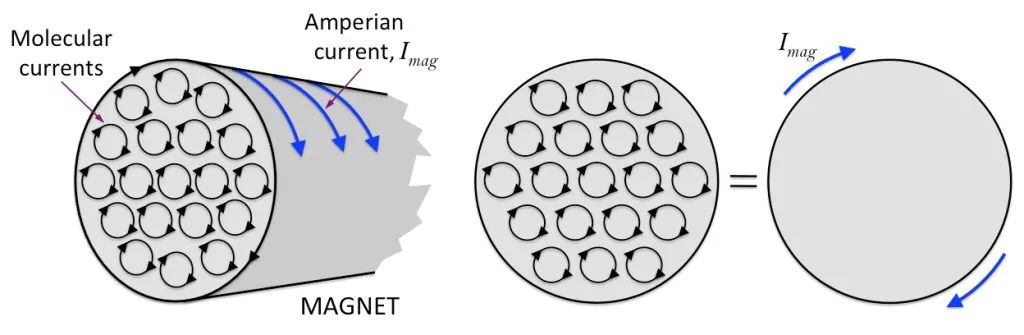

이를 바탕으로 막대 자석은 통전된 솔레노이드와 같다고 생각할 수 있습니다. 즉, 자석의 표면에 얽힌 보이지 않는 전류가 있습니다! 이러한 종류의 전류는 연결하여 사용할 수 없습니다. 그것은 자석의 표면에 국한됩니다. 우리는 그것을 “결합 전류” 또는 “자화 전류”라고 부릅니다.

Therefore, the magnetizing current is a current, because it is the same as the current formed by the movement of real electric charges, which can equivalently generate a magnetic field!

변위전류를 다시 살펴보자.

According to the Ampere’s loop theorem, the integral of the magnetic field strength on a closed path is equal to the flux of the current density on any curved surface bounded by this path, that is, this theorem is called Stokes’ theorem in mathematics. It tells us that the integral of a vector along any closed path must be equal to the flux of its curl (here) to any surface bounded by the closed path.

수학은 수학적 정리이기 때문에 항상 정확해야 합니다. 수학은 공리를 기반으로 하는 논리 시스템이기 때문입니다.

따라서 암페어 루프 정리는 항상 성립해야 합니다!

그러나 재능 있는 스코틀랜드 물리학자 Maxwell은 불안정한 전류 회로에 직면했을 때 암페어 루프 정리가 모순된다는 것을 발견했습니다.

일반적으로 불안정한 전류는 커패시터의 충전 및 방전 중에 발생합니다. 아래 그림과 같이 짧은 커패시터 충전 시간 동안 불안정한 전류가 발생합니다.

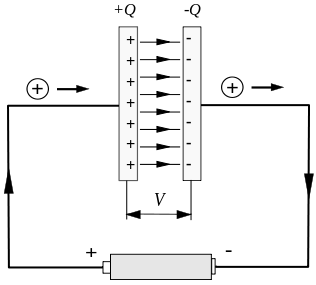
그러나 커패시터 판 사이의 회로가 분리되어 심각한 문제가 발생합니다.

Suppose we consider a closed path that bypasses the wire, as shown in the figure below, the circle marked by C, and the curved surface with it as the boundary can be arbitrarily selected. In the figure, the circular plane enclosed by C itself and across the capacitor are selected. The curved surface of the left plate.

원형 표면에 따르면 곡면에 따라 알 수 있지만 자기장 강도의 루프 적분으로 그 값이 결정되어야 합니다!

수행하는 방법?

Maxwell은 Ampere의 루프 정리가 확립되어야 한다고 믿습니다. 이제 문제가 생겼습니다. 그것은 전류의 일부가 이전에 우리가 발견한 적이 없었기 때문일 것입니다. 그러나 그것은 존재합니다!

그렇다면 현재의이 부분을 찾는 방법은 무엇입니까?

판 사이에 문제가 있으므로 판 사이에서 시작하십시오.

분석을 통해 Maxwell은 충전 또는 방전에 관계없이 전류의 크기 및 방향과 동기화되는 커패시터 플레이트 사이에 항상 물리량이 있음을 발견했습니다. 이것은 전기 변위 벡터의 자속의 시간 도함수, 즉 변위 전류로 정의됩니다.

이 부분이 이전에 발견되지 않은 전류의 일부라고 생각하면 완전한 전류는 현재입니다. 즉, 판 사이의 회로가 단선되어도 전기 변위 플럭스의 미분과 전류의 합이 전체적으로 , 전류의 연속성을 항상 보장합니다.

Going back to the previous contradiction, we now know that, according to the requirements of Stokes’ theorem, when calculating the flux of current density for a closed surface, the density of displacement current should also be considered, that is, the complete ampere loop theorem is therefore, By “discovering” this new current component, the crisis of the Ampere Loop Theorem is resolved!

여기서 “서론”을 사용하지 않고 “발견”을 사용하는 이유입니다. 제가 강조하고 싶은 것은 이러한 전류는 수학적 보상이 아니라 실제 존재하지만 이전에 발견된 적이 없다는 것입니다.

Why does it exist in the first place? Because it acts as an electric current, like a conduction current, it excites a magnetic field equivalently, except that there is no movement of electric charges, no wire is required, and no Joule heat can be generated, so it has been ignored!

But it actually exists by itself, just keep a low profile, it has been silently exciting the magnetic field there all the time!

In other words, when we face a magnetic field, the original definition of current is too narrow. The essence of electric current is not the movement of electric charge, it should be something that can excite a magnetic field.

So far, the several forms of current have been introduced. They all exist objectively, and what they have in common is that all currents can equally excite the magnetic field.