Quel est le courant électrique ? Rappelons d’abord, quelle est la définition du courant que nous avons apprise ?

Tout simplement, le mouvement directionnel des particules chargées dans un conducteur est un courant électrique.

Ce n’est que lorsqu’une substance a des particules chargées qui peuvent se déplacer librement qu’elle peut transmettre du courant électrique, c’est-à-dire conduire l’électricité. Ces particules chargées qui participent à la conduction sont appelées porteurs. Pour les métaux, par exemple, seuls les électrons externes des atomes peuvent jouer le rôle de porteurs.

Le « mouvement directionnel » dans la définition du courant électrique est souvent mal compris. Beaucoup de gens pensent que cela fait référence à un mouvement dans une certaine direction, bien sûr que non ! Le sens de déplacement des électrons dans le circuit alternatif ne change-t-il pas ?

En fait, la course d’orientation est relative au « mouvement aléatoire » !

Puisque les électrons sont des particules microscopiques, ils doivent être en mouvement thermique tout le temps. Le mouvement thermique est un mouvement aléatoire, comme le montre la figure ci-dessous.

Ce mouvement est en fait très rapide. Par exemple, dans les métaux à température ambiante, la vitesse du mouvement thermique électronique est de l’ordre de centaines de kilomètres par seconde !

Si vous regardez attentivement ce mouvement aléatoire, vous constaterez que la direction du mouvement de chaque particule est aléatoire à tout moment. Si vous additionnez les vecteurs de vitesse de ces particules, le résultat est presque nul.

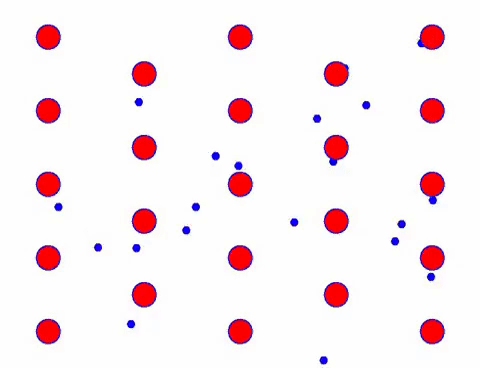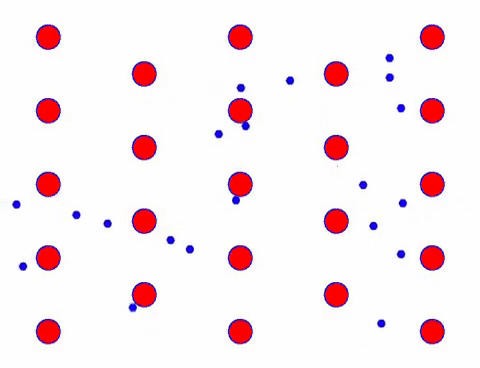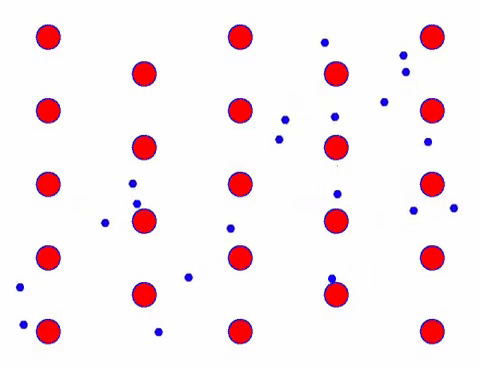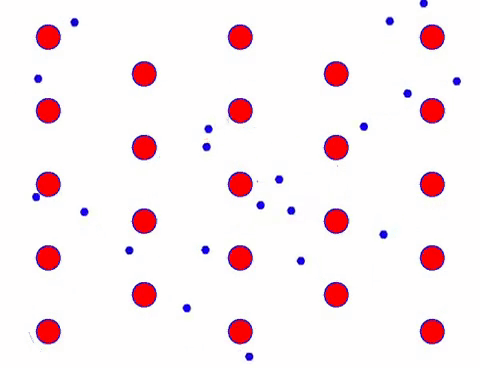
Ajoutez maintenant un champ électrique au conducteur et l’électron superpose un mouvement directionnel sur la base d’un mouvement aléatoire. En supposant que le champ électrique soit à gauche pendant un certain temps, le mouvement des électrons ressemble à ce qui suit. Les boules rouges représentent les atomes métalliques sur le réseau cristallin et les points rapides représentent les électrons libres.

Est-ce que ça a l’air rapide? C’est parce que le mouvement électronique est vraiment rapide ! Mais en fait, le mouvement aléatoire, qui en représente une grande partie, ne contribue pas au courant. Lorsque le mouvement aléatoire est éliminé, le reste est exactement comme le regard lent ci-dessous.

En effet, le mouvement directionnel des électrons est beaucoup plus lent que la vitesse du mouvement thermique. Ce mouvement de « broyage » des électrons est appelé dérive, ou « dérive ». Parfois, les électrons courent dans la direction opposée à cause de collisions avec des atomes. Mais en général, les électrons se déplacent dans une direction.

Si le champ électrique change de direction, la direction de la dérive des électrons changera également.

Par conséquent, ce type de mouvement directionnel signifie que la somme des vitesses de tous les électrons participant à la conduction à un certain moment n’est pas nulle, mais est généralement dans une certaine direction. Ce sens peut être modifié à tout moment, et c’est le cas du courant alternatif.

Par conséquent, le courant n’est pas tant le « mouvement directionnel » de la charge électrique que le « mouvement collectif » de la charge électrique.

L’amplitude du courant dans le conducteur est exprimée par l’intensité du courant. L’intensité du courant est définie comme la quantité d’électricité traversant la section transversale du conducteur dans une unité de temps, à savoir

Nous avons appris certaines quantités physiques qui contiennent le mot « intensité », telles que l’intensité du champ électrique et l’intensité de l’induction magnétique. Ils représentent généralement la répartition par unité de temps, unité de surface (ou unité de volume, unité d’angle solide). Cependant, le mot « intensité » dans l’intensité actuelle ne reflète pas la répartition actuelle de la zone.

En fait, une autre quantité physique est responsable de la distribution du courant dans la zone, qui est la densité de courant.

Puisque l’essence du courant électrique est le mouvement directionnel de la charge électrique, il doit y avoir une certaine relation entre l’intensité du courant et la vitesse de dérive !

Afin d’obtenir cette relation, nous devons d’abord clarifier un concept de concentration en porteurs, c’est-à-dire le nombre de porteurs dans une unité de volume, qui s’exprime par .

On suppose que la section transversale du conducteur est, la concentration en porteurs est, la vitesse de dérive est et la charge chargée est.

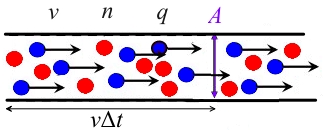
Ensuite, la charge dans le conducteur sur le côté gauche de la surface est, et ces charges traverseront la surface dans un certain laps de temps, donc

Il s’agit d’une expression microscopique de l’intensité du courant.

La densité de courant est la répartition du courant dans la zone, donc l’amplitude de la densité de courant est, mais elle est définie comme un vecteur, et la direction est la direction du vecteur de vitesse de dérive des porteurs chargés positivement, donc la dérive des électrons dans le le métal peut être obtenu à partir de cette vitesse, comme exemple ci-dessous.

Considérons un fil de cuivre, en supposant que chaque atome de cuivre contribue à un électron en tant que porteur. Il y a 1 mole de cuivre, son volume est, la masse molaire est, la densité est, alors la concentration en porteurs du fil de cuivre est

Où est la constante d’Avogadro. La densité du cuivre est trouvée, et la valeur obtenue par substitution est d’environ unité/mètre cube.

En supposant que le rayon du fil de cuivre est de 0.8 mm, le courant circulant est de 15 A, = 1.6 C, et la vitesse de dérive des électrons est calculée comme suit

On peut voir que la vitesse de dérive des électrons est en effet très faible.

Pour ceux qui étudient les circuits, ce qui précède est la définition complète du courant.

Mais en physique, la définition ci-dessus du courant n’est en fait qu’une définition étroite. Les courants plus généraux ne se limitent pas aux conducteurs, tant que le mouvement des charges électriques est courant. Par exemple, lorsque les électrons d’un atome d’hydrogène se déplacent autour du noyau, un courant électrique se forme sur son orbite.

Supposons que le montant de la charge électronique est et que la période de mouvement est. Ensuite, chaque fois que cela s’écoule, une telle quantité de charge traverse n’importe quelle section transversale de la boucle, de sorte que l’intensité du courant est basée sur la relation entre la période, la fréquence et la vitesse angulaire, et le courant peut également être exprimé sous la forme

Pour un autre exemple, un disque de métal chargé, tournant autour de son axe, forme également des courants de boucle avec des rayons différents.

Ce type de courant n’est pas un courant de conduction normal et ne peut pas générer de chaleur Joule ! Impossible de former un vrai circuit.

Sinon, pourriez-vous me donner un calcul de la quantité de chaleur joule générée par seconde par les électrons de l’atome d’hydrogène ?

En fait, le courant dans le vide ne satisfait pas la loi d’Ohm. Parce que, pour le courant électrique formé par le mouvement des particules chargées dans le vide, les porteurs ne sont pas entrés en collision de la même manière que le réseau du métal, de sorte que le vide n’a ni résistance ni conductance.

Le mouvement des charges électriques génère du courant électrique et la charge électrique elle-même excite le champ électrique. C’est facile de provoquer un malentendu. Beaucoup de gens pensent donc que le champ électrique des particules chargées qui forment le courant électrique doit être exposé. Mais en fait, pour le courant de conduction dans un conducteur général, les porteurs circulent sur un fond composé d’un grand nombre d’ions métalliques chargés positivement, et le conducteur lui-même est neutre !

On appelle souvent ce type de courant spécial un « courant équivalent ». L’équivalent ici signifie qu’il génère un champ magnétique au même titre qu’un courant de conduction ordinaire !

Rappel : Ne pas confondre ici le « courant équivalent » avec le « circuit équivalent » en analyse de circuit

En fait, lorsque nous avons étudié le champ magnétique pour la première fois, le courant électrique dans la loi de Biot-Saffar était le courant électrique généralisé qui contenait ce courant équivalent. Bien entendu, le courant de conduction dans les équations de Maxwell fait également référence au courant généralisé.

Ceux qui ont étudié l’effet photoélectrique savent que lorsque le photoélectron dérive de la cathode vers l’anode, si l’on ignore l’influence de l’air, ce courant est provoqué par le mouvement des charges électriques dans le vide, et il n’y a pas de résistance, donc il n’est pas limité par la loi d’Ohm.

Alors, est-ce la seule chose à propos du courant électrique en physique ?

Non! Il existe également deux types, à savoir le courant magnétisant et le courant de déplacement.

Ce sont aussi deux courants équivalents, qui, comme leur nom l’indique, sont également introduits pour expliquer le magnétisme. Autrement dit, ils ont rompu avec la caractéristique fondamentale du « mouvement de charge » actuel !

C’est incroyable ! Il n’y a pas de mouvement de charge électrique, alors pourquoi peut-on l’appeler courant électrique ?

Ne vous inquiétez pas, et écoutez-moi lentement.

Regardons d’abord le courant magnétisant.

Il a été constaté que le magnétisme est causé par le mouvement de l’électricité (sans tenir compte pour le moment de l’explication du magnétisme par les propriétés intrinsèques du spin). Pour expliquer le magnétisme naturel, le physicien français Ampère a avancé l’hypothèse d’une « circulation moléculaire ».

Comme le montre la figure ci-dessous, tout atome ou molécule peut être considéré comme ayant une charge électrique tournant autour du centre, formant un minuscule courant de boucle, c’est-à-dire une “circulation moléculaire”.

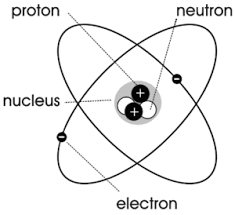
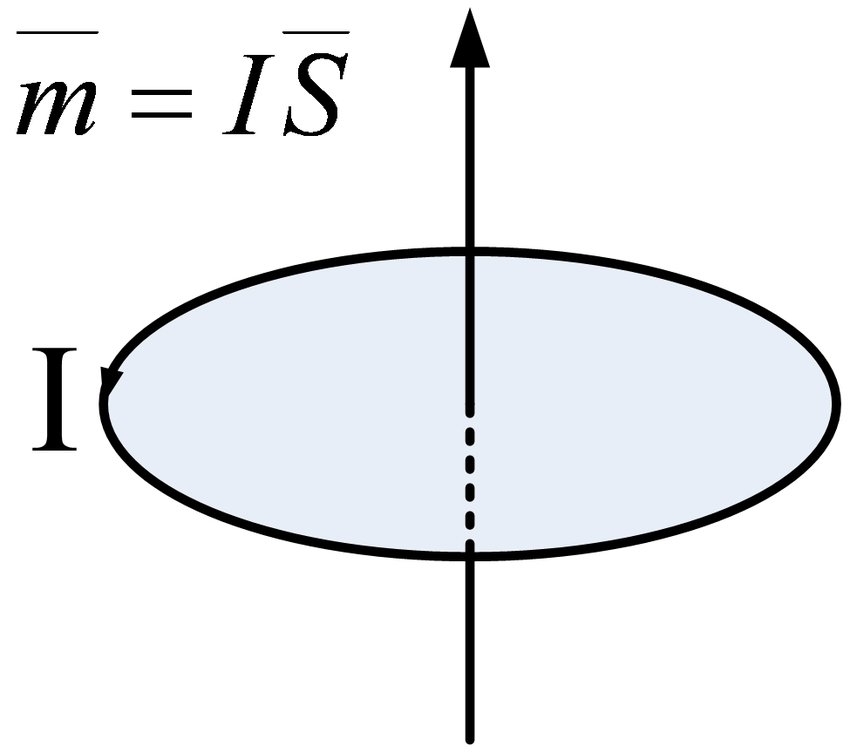
Selon la loi selon laquelle le courant électrique excite le champ magnétique, cette circulation moléculaire produira une quantité physique appelée moment magnétique. Sa taille est la zone délimitée par la circulation moléculaire multipliée par le courant équivalent de la circulation moléculaire, et sa direction est dans une relation en spirale à droite avec la direction de la circulation, à savoir

De toute évidence, la direction du moment magnétique est exactement le long de la direction du champ magnétique formé par le courant circulant

.

Dans des circonstances normales, l’arrangement de la circulation moléculaire d’une substance est chaotique, donc la substance n’est pas magnétique, comme indiqué sur le côté gauche de la figure ci-dessous. Lorsqu’elles sont soumises à un champ magnétique externe, ces circulations moléculaires seront approximativement soigneusement agencées. Comme le montre le côté droit de la figure ci-dessous, leurs moments magnétiques sont disposés dans une direction autant que possible, tout comme d’innombrables petites aiguilles magnétiques rassemblées pour former un champ magnétique total, et tout le matériau qui les compose devient magnétique.

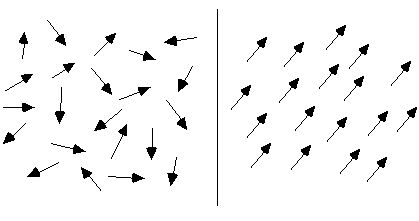
Supposons qu’il y ait un aimant cylindrique, que la circulation moléculaire interne soit soigneusement agencée et que les sections de chaque circulation moléculaire au bord de la section magnétique soient connectées ensemble pour former une grande circulation, comme le montre la figure ci-dessous.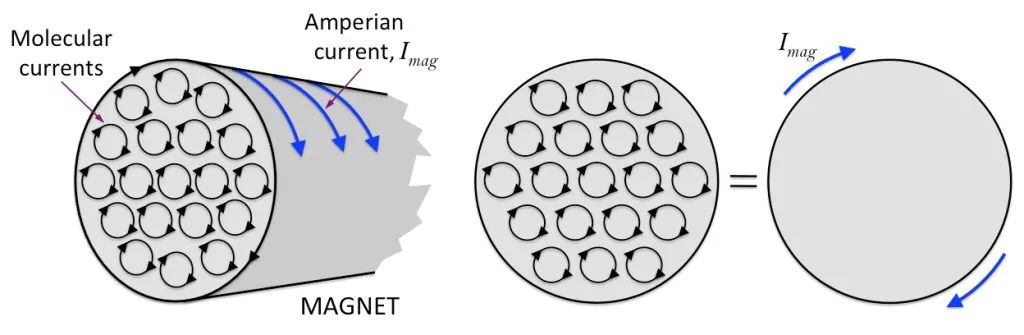

Sur cette base, nous pouvons penser qu’un barreau magnétique est comme un solénoïde sous tension. En d’autres termes, il y a un courant invisible intriqué à la surface de l’aimant ! Ce type de courant ne peut pas être connecté et utilisé. Il est confiné à la surface de l’aimant. Nous l’appelons “courant de liaison” ou “courant magnétisant”.

Par conséquent, le courant magnétisant est un courant, car c’est le même que le courant formé par le mouvement de charges électriques réelles, qui peut générer de manière équivalente un champ magnétique !

Regardons à nouveau le courant de déplacement.

Selon le théorème de la boucle d’Ampère, l’intégrale de l’intensité du champ magnétique sur un chemin fermé est égale au flux de la densité de courant sur toute surface courbe délimitée par ce chemin, c’est-à-dire que ce théorème est appelé théorème de Stokes en mathématiques. Il nous dit que l’intégrale d’un vecteur le long de tout chemin fermé doit être égale au flux de sa boucle (ici) à toute surface délimitée par le chemin fermé.

Puisqu’il s’agit d’un théorème mathématique, il doit toujours être correct, car les mathématiques sont un système logique basé sur des axiomes.

Par conséquent, le théorème de boucle d’Ampère doit toujours tenir !

Cependant, le talentueux physicien écossais Maxwell a découvert que face à un circuit de courant instable, le théorème de la boucle d’Ampère était contradictoire.

Le courant instable typique se produit pendant la charge et la décharge du condensateur. Comme le montre la figure ci-dessous, il existe un courant instable pendant la courte période de charge du condensateur.

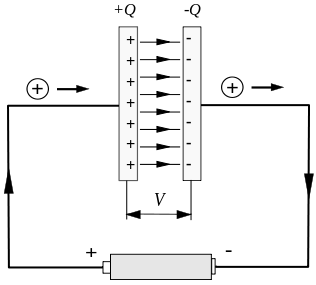
Mais le circuit est déconnecté entre les plaques du condensateur, ce qui causera un grave problème.

Supposons que nous considérions un chemin fermé qui contourne le fil, comme le montre la figure ci-dessous, le cercle marqué par C et la surface incurvée avec comme limite peuvent être choisis arbitrairement. Sur la figure, le plan circulaire entouré par C lui-même et à travers le condensateur est sélectionné. La surface incurvée de la plaque gauche.

D’après la surface circulaire, on peut voir qu’en fonction de la surface incurvée, mais en tant qu’intégrale de boucle de l’intensité du champ magnétique, sa valeur doit être déterminée !

Comment faire?

Maxwell pense que le théorème de la boucle d’Ampère doit être établi. Maintenant qu’il y a un problème, ce doit être parce qu’une partie du courant n’a pas été découverte par nous auparavant, mais elle existe !

Alors, comment découvrir cette partie du courant ?

Puisque le problème se situe entre les plaques, commencez par entre les plaques.

Grâce à une analyse, Maxwell a découvert que, indépendamment de la charge ou de la décharge, il existe à tout moment une quantité physique entre les plaques du condensateur qui est synchronisée avec l’amplitude et la direction du courant. C’est la dérivée temporelle du flux du vecteur de déplacement électrique, c’est-à-dire qu’il est défini comme le courant de déplacement.

Si l’on considère que cette partie est la partie du courant qui n’a pas été découverte auparavant, alors le courant complet est maintenant. C’est-à-dire que, bien que le circuit entre les plaques soit déconnecté, la dérivée du flux de déplacement électrique et la somme du courant ensemble, dans leur ensemble, assurent la continuité du courant à tout moment.

En revenant à la contradiction précédente, nous savons maintenant que, selon les exigences du théorème de Stokes, lors du calcul de la densité de flux de courant pour une surface fermée, la densité de courant de déplacement doit également être considérée, c’est-à-dire la boucle d’ampères complète Le théorème est donc, En « découvrant » cette nouvelle composante actuelle, la crise du théorème de boucle d’Ampère est résolue !

La raison pour laquelle « introduction » n’est pas utilisée ici, mais « découverte » est utilisée ici. Ce que je veux souligner, c’est que ce genre de courant n’est pas une compensation mathématique, mais une chose réelle, mais elle n’a pas été découverte auparavant.

Pourquoi existe-t-il en premier lieu ? Parce qu’il agit comme un courant électrique, comme un courant de conduction, il excite un champ magnétique de manière équivalente, sauf qu’il n’y a aucun mouvement de charges électriques, aucun fil n’est requis et aucune chaleur Joule ne peut être générée, donc il a été ignoré !

Mais il existe en fait par lui-même, gardez juste un profil bas, il a excité silencieusement le champ magnétique là-bas tout le temps !

En d’autres termes, lorsque nous sommes confrontés à un champ magnétique, la définition originale du courant est trop étroite. L’essence du courant électrique n’est pas le mouvement de la charge électrique, ce devrait être quelque chose qui peut exciter un champ magnétique.

Jusqu’à présent, plusieurs formes de courant ont été introduites. Ils existent tous objectivement, et ce qu’ils ont en commun, c’est que tous les courants peuvent également exciter le champ magnétique.