তড়িৎ প্রবাহ কি? প্রথমে প্রত্যাহার করুন, আমরা শিখেছি বর্তমানের সংজ্ঞা কী?

খুব সহজভাবে, একটি পরিবাহীতে আধানযুক্ত কণার দিকনির্দেশনামূলক গতি একটি বৈদ্যুতিক প্রবাহ।

শুধুমাত্র যখন একটি পদার্থের চার্জযুক্ত কণা থাকে যা অবাধে চলাচল করতে পারে, এটি বৈদ্যুতিক প্রবাহ প্রেরণ করতে পারে-অর্থাৎ, বিদ্যুৎ পরিচালনা করতে পারে। এই চার্জযুক্ত কণাগুলি যা পরিবাহিতে অংশ নেয় তাদের বাহক বলা হয়। ধাতুগুলির জন্য, উদাহরণস্বরূপ, শুধুমাত্র পরমাণুর বাইরের ইলেকট্রন বাহক হিসাবে কাজ করতে পারে।

বৈদ্যুতিক প্রবাহের সংজ্ঞায় “দিকনির্দেশক আন্দোলন” প্রায়শই ভুল বোঝা যায়। অনেকে মনে করেন এটি একটি নির্দিষ্ট দিক দিয়ে আন্দোলন বোঝায়, অবশ্যই না! এসি সার্কিটে ইলেকট্রনের গতিবিধি কি পরিবর্তন হয় না?

আসলে, ওরিয়েন্টিয়ারিং “এলোমেলো আন্দোলন” এর সাথে আপেক্ষিক!

যেহেতু ইলেক্ট্রনগুলি আণুবীক্ষণিক কণা, তাই তাদের সর্বদা তাপীয় গতিতে থাকতে হবে। তাপীয় গতি হল একটি এলোমেলো গতি, যা নীচের চিত্রে দেখানো হয়েছে।

এই আন্দোলন আসলে খুব দ্রুত. উদাহরণস্বরূপ, ঘরের তাপমাত্রায় ধাতুগুলিতে, বৈদ্যুতিন তাপীয় চলাচলের গতি প্রতি সেকেন্ডে শত শত কিলোমিটার!

আপনি যদি এই এলোমেলো গতিবিধিটি ঘনিষ্ঠভাবে লক্ষ্য করেন তবে আপনি দেখতে পাবেন যে প্রতিটি কণার গতিবিধি যে কোনও মুহূর্তে এলোমেলো। আপনি যদি এই কণার বেগ ভেক্টর যোগ করেন, ফলাফল প্রায় শূন্য হয়।

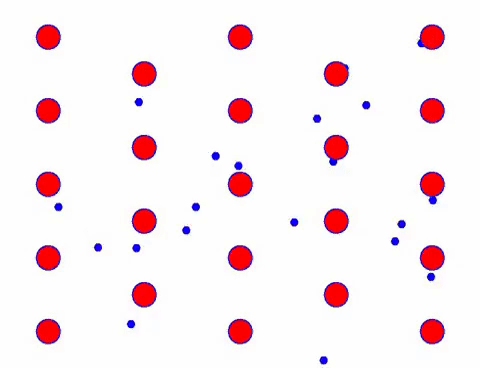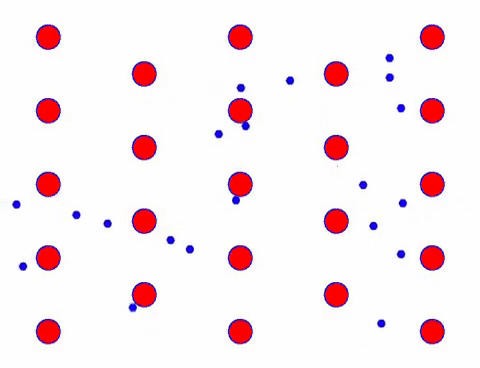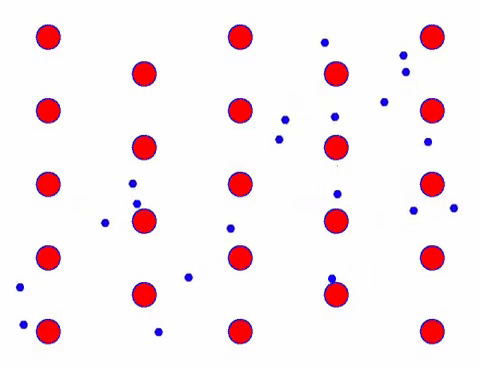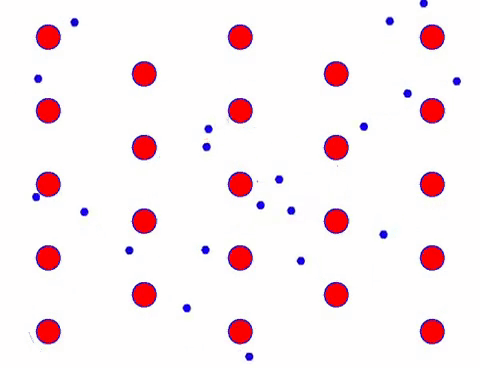
এখন পরিবাহীতে একটি বৈদ্যুতিক ক্ষেত্র যোগ করুন, এবং ইলেকট্রন এলোমেলো আন্দোলনের ভিত্তিতে একটি দিকনির্দেশক আন্দোলনকে সুপারইম্পোজ করে। একটি নির্দিষ্ট সময়ের জন্য বৈদ্যুতিক ক্ষেত্রটি বাম দিকে রয়েছে বলে ধরে নিলে, ইলেকট্রনের গতিবিধি নিচের মত দেখায়। লাল বলগুলি স্ফটিক জালিতে ধাতব পরমাণুগুলিকে প্রতিনিধিত্ব করে এবং দ্রুত চলমান বিন্দুগুলি মুক্ত ইলেকট্রনকে প্রতিনিধিত্ব করে।

এটা কি দ্রুত দেখায়? কারণ ইলেকট্রনিক আন্দোলন সত্যিই দ্রুত! কিন্তু প্রকৃতপক্ষে, এলোমেলো গতি, যা এটির একটি বড় অনুপাতের জন্য দায়ী, স্রোতে অবদান রাখে না। যখন এলোমেলো গতি বাদ দেওয়া হয়, বাকিটা ঠিক নিচের ধীরগতির মত।

প্রকৃতপক্ষে, ইলেক্ট্রনের দিকনির্দেশক গতি তাপীয় গতির গতির চেয়ে অনেক ধীর। ইলেক্ট্রনগুলির এই “নাকাল” আন্দোলনকে ড্রিফট বা “ড্রিফট” বলা হয়। কখনও কখনও, পরমাণুর সাথে সংঘর্ষের কারণে ইলেকট্রনগুলি বিপরীত দিকে ছুটবে। কিন্তু সাধারণভাবে, ইলেকট্রন এক দিকে চলে।

বৈদ্যুতিক ক্ষেত্রের দিক পরিবর্তন হলে, ইলেকট্রন প্রবাহের দিকও পরিবর্তিত হবে।

অতএব, এই ধরণের দিকনির্দেশক আন্দোলনের অর্থ হল একটি নির্দিষ্ট সময়ে পরিবাহিতে অংশগ্রহণকারী সমস্ত ইলেকট্রনের গতির সমষ্টি শূন্য নয়, তবে সাধারণত একটি নির্দিষ্ট দিকে থাকে। এই দিকটি যে কোনও সময় পরিবর্তন করা যেতে পারে, এবং এটি বিকল্প কারেন্টের ক্ষেত্রে।

অতএব, কারেন্ট বৈদ্যুতিক আধানের “দিকনির্দেশক আন্দোলন” নয় যতটা এটি বৈদ্যুতিক চার্জের “সম্মিলিত আন্দোলন”।

কন্ডাকটরে কারেন্টের মাত্রা বর্তমান তীব্রতা দ্বারা প্রকাশ করা হয়। বর্তমান তীব্রতা একটি ইউনিট সময়ে কন্ডাকটরের ক্রস-সেকশনের মধ্য দিয়ে যাওয়া বিদ্যুতের পরিমাণ হিসাবে সংজ্ঞায়িত করা হয়, যথা

আমরা কিছু ভৌত পরিমাণ শিখেছি যেগুলিতে “তীব্রতা” শব্দটি রয়েছে, যেমন বৈদ্যুতিক ক্ষেত্রের তীব্রতা এবং চৌম্বকীয় আবেশ তীব্রতা। তারা সাধারণত প্রতি ইউনিট সময়, ইউনিট এলাকা (বা একক ভলিউম, একক কঠিন কোণ) প্রতি ভাগের প্রতিনিধিত্ব করে। যাইহোক, বর্তমান তীব্রতায় “তীব্রতা” শব্দটি এলাকার বর্তমান বন্টনকে প্রতিফলিত করে না।

প্রকৃতপক্ষে, অন্য একটি ভৌত ​​পরিমাণ ক্ষেত্রবিশেষে কারেন্ট বিতরণের জন্য দায়ী, যা বর্তমান ঘনত্ব।

যেহেতু বৈদ্যুতিক প্রবাহের সারমর্ম হল বৈদ্যুতিক চার্জের দিকনির্দেশনামূলক গতি, তাই কারেন্টের তীব্রতা এবং প্রবাহের গতির মধ্যে একটি নির্দিষ্ট সম্পর্ক থাকতে হবে!

এই সম্পর্ক প্রাপ্ত করার জন্য, আমাদের প্রথমে একটি ধারণা-ক্যারিয়ার ঘনত্ব স্পষ্ট করতে হবে, অর্থাৎ, একটি ইউনিট আয়তনে বাহকের সংখ্যা, যা  দ্বারা প্রকাশ করা হয়।

এটা অনুমান করা হয় যে কন্ডাকটর ক্রস সেকশন হল, ক্যারিয়ারের ঘনত্ব হল, ড্রিফট বেগ হল, এবং চার্জ করা চার্জ হল।

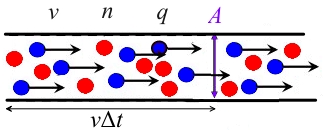
তারপর পৃষ্ঠের বাম দিকে পরিবাহীতে চার্জ থাকে এবং এই চার্জগুলি একটি নির্দিষ্ট সময়ের মধ্যে পৃষ্ঠের মধ্য দিয়ে যাবে, তাই

এটি বর্তমান তীব্রতার একটি মাইক্রোস্কোপিক অভিব্যক্তি।

কারেন্ট ডেনসিটি হল ক্ষেত্রফল থেকে কারেন্টের বিভাজন, তাই কারেন্টের ঘনত্বের মাত্রা হল, তবে এটি একটি ভেক্টর হিসাবে সংজ্ঞায়িত করা হয়, এবং দিক হল ধনাত্মক চার্জযুক্ত বাহকগুলির ড্রিফ্ট বেগ ভেক্টরের দিক, তাই ইলেকট্রনগুলির প্রবাহ ধাতু এই গতি থেকে প্রাপ্ত করা যেতে পারে, নীচের একটি উদাহরণ হিসাবে.

একটি তামার তারের কথা বিবেচনা করুন, অনুমান করুন যে প্রতিটি তামার পরমাণু একটি বাহক হিসাবে একটি ইলেক্ট্রনকে অবদান রাখে। তামার 1 মোল আছে, এর আয়তন হল, মোলার ভর হল, ঘনত্ব হল, তাহলে তামার তারের বাহক ঘনত্ব হল

কোথায় অ্যাভোগাড্রোর ধ্রুবক। তামার ঘনত্ব পাওয়া যায়, এবং প্রতিস্থাপন দ্বারা প্রাপ্ত মান প্রায় একক/ঘন মিটার।

ধরে নিলাম যে তামার তারের ব্যাসার্ধ 0.8 মিমি, তড়িৎ প্রবাহ 15A, =1.6 সি, এবং ইলেকট্রনের প্রবাহ বেগ হিসাবে গণনা করা হয়

এটা দেখা যায় যে ইলেকট্রনের প্রবাহের গতি আসলেই খুব ছোট।

যারা সার্কিট অধ্যয়ন করেন তাদের জন্য, উপরেরটি কারেন্টের সম্পূর্ণ সংজ্ঞা।

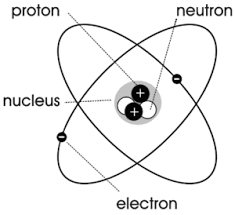
কিন্তু পদার্থবিজ্ঞানে, কারেন্টের উপরোক্ত সংজ্ঞা আসলে একটি সংকীর্ণ সংজ্ঞা। যতক্ষণ বৈদ্যুতিক চার্জের চলন ততক্ষণ পর্যন্ত কন্ডাক্টরের মধ্যে সীমাবদ্ধ নয় আরও সাধারণ স্রোত। উদাহরণস্বরূপ, যখন একটি হাইড্রোজেন পরমাণুর ইলেকট্রন নিউক্লিয়াসের চারপাশে ঘোরে, তখন তার কক্ষপথে একটি বৈদ্যুতিক প্রবাহ তৈরি হয়।

ধরুন ইলেকট্রনিক চার্জের পরিমাণ এবং চলাফেরার সময়কাল। তারপর প্রতিবার যখন অতিবাহিত হয়, লুপের যেকোন ক্রস সেকশনের মধ্য দিয়ে এত বেশি পরিমাণে চার্জ যায়, তাই বর্তমান তীব্রতা পিরিয়ড, ফ্রিকোয়েন্সি এবং কৌণিক বেগের মধ্যে সম্পর্কের উপর ভিত্তি করে এবং কারেন্টকে এভাবে প্রকাশ করা যেতে পারে

আরেকটি উদাহরণের জন্য, একটি চার্জযুক্ত ধাতব ডিস্ক, তার অক্ষের চারপাশে ঘূর্ণায়মান, এছাড়াও বিভিন্ন রেডিআই সহ লুপ স্রোত গঠন করে।

এই ধরনের কারেন্ট একটি স্বাভাবিক পরিবাহী কারেন্ট নয় এবং জুল তাপ উৎপন্ন করতে পারে না! একটি বাস্তব সার্কিট গঠন করতে পারে না.

অন্যথায়, আপনি কি আমাকে হাইড্রোজেন পরমাণুর ইলেকট্রন দ্বারা প্রতি সেকেন্ডে কত জুল তাপ উৎপন্ন হয় তার একটি হিসাব দেবেন?

প্রকৃতপক্ষে, ভ্যাকুয়ামে কারেন্ট ওহমের সূত্রকে সন্তুষ্ট করে না। কারণ, ভ্যাকুয়ামে আধানযুক্ত কণার গতিবিধি দ্বারা গঠিত বৈদ্যুতিক প্রবাহের জন্য, বাহকগুলি ধাতুর জালির মতো সংঘর্ষ হয় না, তাই ভ্যাকুয়ামের কোনও প্রতিরোধ নেই এবং কোনও পরিবাহিতা নেই।

বৈদ্যুতিক চার্জের চলাচল বৈদ্যুতিক প্রবাহ উৎপন্ন করে এবং বৈদ্যুতিক চার্জ নিজেই বৈদ্যুতিক ক্ষেত্রকে উত্তেজিত করে। এটি একটি ভুল বোঝাবুঝি সৃষ্টি করা সহজ। তাই অনেকে মনে করেন যে চার্জযুক্ত কণাগুলির বৈদ্যুতিক ক্ষেত্র যা বৈদ্যুতিক প্রবাহ গঠন করে তা অবশ্যই উন্মুক্ত হওয়া উচিত। কিন্তু প্রকৃতপক্ষে, একটি সাধারণ পরিবাহীতে পরিবাহী কারেন্টের জন্য, বাহক একটি পটভূমিতে প্রবাহিত হয় যা প্রচুর পরিমাণে ধনাত্মক চার্জযুক্ত ধাতব আয়ন দ্বারা গঠিত এবং পরিবাহী নিজেই নিরপেক্ষ!

আমরা প্রায়ই এই ধরনের বিশেষ স্রোতকে “সমতুল্য কারেন্ট” বলি। এখানে সমতুল্য মানে এটি একটি সাধারণ পরিবাহী কারেন্টের মতো একই ভিত্তিতে একটি চৌম্বক ক্ষেত্র তৈরি করে!

অনুস্মারক: সার্কিট বিশ্লেষণে “সমতুল্য বর্তনী” এর সাথে এখানে “সমতুল্য কারেন্ট” কে বিভ্রান্ত করবেন না

প্রকৃতপক্ষে, যখন আমরা প্রথম চৌম্বক ক্ষেত্র অধ্যয়ন করি, তখন বায়োট-সাফারের সূত্রে বৈদ্যুতিক প্রবাহ ছিল সাধারণীকৃত বৈদ্যুতিক প্রবাহ যা এই সমতুল্য প্রবাহ ধারণ করে। অবশ্যই, ম্যাক্সওয়েলের সমীকরণে পরিবাহী তড়িৎও সাধারণীকৃত কারেন্টকে নির্দেশ করে।

যারা ফটোইলেক্ট্রিক প্রভাব অধ্যয়ন করেছেন তারা জানেন যে ফটোইলেক্ট্রন যখন ক্যাথোড থেকে অ্যানোডে চলে যায়, যদি বাতাসের প্রভাবকে উপেক্ষা করা হয়, এই কারেন্টটি ভ্যাকুয়ামে বৈদ্যুতিক চার্জের চলাচলের কারণে ঘটে এবং কোন প্রতিরোধ নেই, তাই এটি ওহমের আইন দ্বারা সীমাবদ্ধ নয়।

তাহলে, পদার্থবিজ্ঞানে কি বৈদ্যুতিক প্রবাহ সম্পর্কে এটাই কি?

না! এছাড়াও দুই প্রকার, যথা ম্যাগনেটাইজিং কারেন্ট এবং ডিসপ্লেসমেন্ট কারেন্ট।

এগুলিও দুটি সমতুল্য স্রোত, যা নাম থেকেই বোঝা যায়, চুম্বকত্ব ব্যাখ্যা করার জন্যও প্রবর্তিত হয়। অন্য কথায়, তারা বর্তমান “চার্জ আন্দোলনের” মৌলিক বৈশিষ্ট্য থেকে দূরে সরে গেছে!

এটা আশ্চর্যজনক! কোন বৈদ্যুতিক চার্জ আন্দোলন নেই, তাহলে এটিকে বৈদ্যুতিক প্রবাহ বলা যাবে কেন?

চিন্তা করবেন না, এবং ধীরে ধীরে আমার কথা শুনুন।

প্রথমে চৌম্বকীয় কারেন্ট দেখি।

এটি পাওয়া গেছে যে চুম্বকত্ব বিদ্যুতের গতিবিধির কারণে ঘটে (আপাতত ঘূর্ণনের অন্তর্নিহিত বৈশিষ্ট্য দ্বারা চুম্বকত্বের ব্যাখ্যা বিবেচনা না করা)। প্রাকৃতিক চুম্বকত্ব ব্যাখ্যা করার জন্য, ফরাসি পদার্থবিজ্ঞানী অ্যাম্পিয়ার “আণবিক সঞ্চালন” এর হাইপোথিসিসটি সামনে রেখেছিলেন।

নীচের চিত্রে যেমন দেখানো হয়েছে, যে কোনো পরমাণু বা অণুকে কেন্দ্রের চারপাশে ঘূর্ণায়মান বৈদ্যুতিক চার্জ হিসাবে বিবেচনা করা যেতে পারে, যা একটি ক্ষুদ্র লুপ কারেন্ট তৈরি করে, অর্থাৎ “আণবিক সঞ্চালন”।

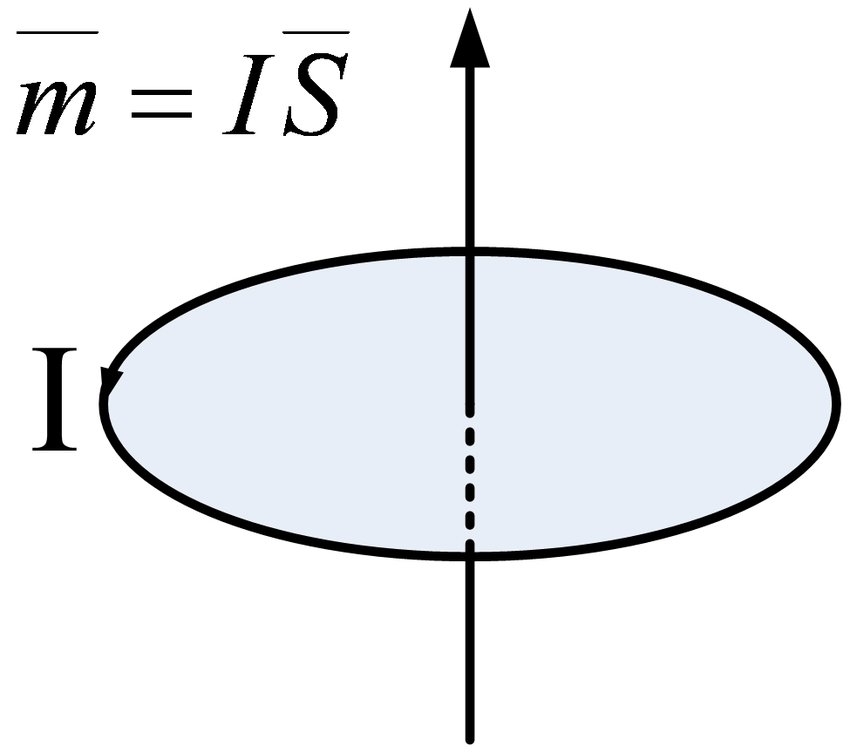
যে আইন অনুসারে বৈদ্যুতিক প্রবাহ চৌম্বক ক্ষেত্রকে উত্তেজিত করে, এই আণবিক সঞ্চালনটি চৌম্বকীয় মোমেন্ট নামে একটি ভৌত ​​পরিমাণ তৈরি করবে। এটির আকার হল আণবিক সঞ্চালন দ্বারা আবদ্ধ এলাকা যা আণবিক সঞ্চালনের সমতুল্য কারেন্ট দ্বারা গুণিত হয় এবং এর দিকটি সঞ্চালনের দিকের সাথে ডান হাতের সর্পিল সম্পর্কের মধ্যে থাকে, যথা

স্পষ্টতই, চৌম্বকীয় মুহূর্তের দিকটি সঞ্চালিত কারেন্ট দ্বারা গঠিত চৌম্বক ক্ষেত্রের দিক বরাবর ঠিক।

.

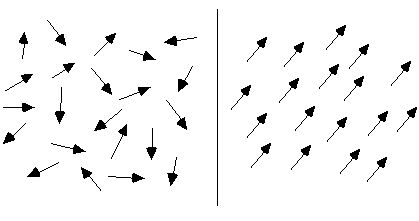
সাধারণ পরিস্থিতিতে, একটি পদার্থের আণবিক সঞ্চালনের বিন্যাস বিশৃঙ্খল, তাই পদার্থটি চৌম্বক নয়, যেমনটি নীচের চিত্রের বাম দিকে দেখানো হয়েছে। বাহ্যিক চৌম্বক ক্ষেত্রের অধীন হলে, এই আণবিক প্রচলনগুলি প্রায় সুন্দরভাবে সাজানো হবে। নীচের চিত্রের ডানদিকে দেখানো হয়েছে, তাদের চৌম্বকীয় মুহূর্তগুলি যথাসম্ভব এক দিকে সাজানো হয়েছে, ঠিক যেমন অসংখ্য ছোট চৌম্বকীয় সূঁচ একত্রিত হয়ে একটি মোট চৌম্বক ক্ষেত্র তৈরি করে এবং তাদের দ্বারা গঠিত পুরো উপাদানটি চৌম্বকীয় হয়ে ওঠে।

ধরুন একটি নলাকার চুম্বক রয়েছে, ভিতরের আণবিক সঞ্চালনটি সুন্দরভাবে সাজানো হয়েছে এবং চুম্বক বিভাগের প্রান্তে প্রতিটি আণবিক সঞ্চালনের বিভাগগুলি একসাথে যুক্ত হয়ে একটি বৃহৎ সঞ্চালন তৈরি করেছে, যেমনটি নীচের চিত্রে দেখানো হয়েছে।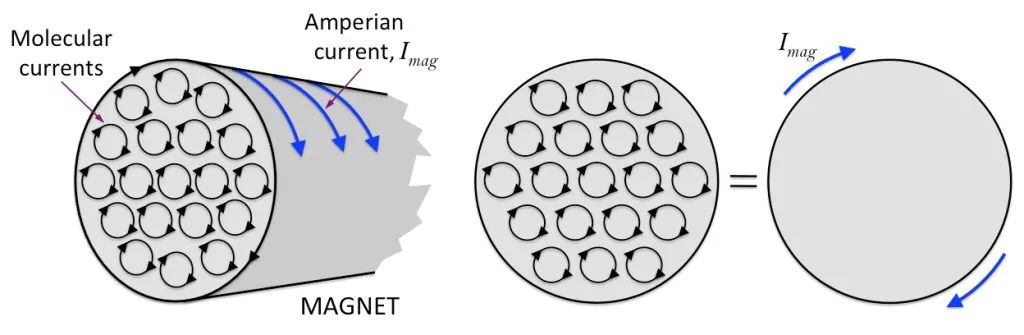

এর উপর ভিত্তি করে, আমরা ভাবতে পারি যে একটি বার চুম্বক একটি শক্তিযুক্ত সোলেনয়েডের মতো। অন্য কথায়, চুম্বকের পৃষ্ঠে একটি অদৃশ্য স্রোত আটকে আছে! এই ধরনের বর্তমান সংযোগ এবং ব্যবহার করা যাবে না. এটি চুম্বকের পৃষ্ঠের মধ্যে সীমাবদ্ধ। আমরা একে বলি “বাইন্ডিং কারেন্ট” বা “চুম্বকীয় কারেন্ট”।

অতএব, চৌম্বকীয় কারেন্ট হল একটি কারেন্ট, কারণ এটি প্রকৃত বৈদ্যুতিক চার্জের চলাচলের দ্বারা গঠিত তড়িৎ প্রবাহের সমান, যা সমানভাবে একটি চৌম্বক ক্ষেত্র তৈরি করতে পারে!

এর স্থানচ্যুতি বর্তমান আবার তাকান.

অ্যাম্পিয়ারের লুপ উপপাদ্য অনুসারে, একটি বদ্ধ পথে চৌম্বক ক্ষেত্রের শক্তির অখণ্ডতা এই পথ দ্বারা আবদ্ধ যেকোনো বাঁকা পৃষ্ঠে বর্তমান ঘনত্বের প্রবাহের সমান, অর্থাৎ এই উপপাদ্যটিকে গণিতে স্টোকসের উপপাদ্য বলা হয়। এটি আমাদের বলে যে কোনও বদ্ধ পথ বরাবর একটি ভেক্টরের অখণ্ডতা অবশ্যই তার কার্ল (এখানে) বন্ধ পথ দ্বারা আবদ্ধ যে কোনও পৃষ্ঠের প্রবাহের সমান হতে হবে।

যেহেতু এটি একটি গাণিতিক উপপাদ্য, তাই এটি সর্বদা সঠিক হতে হবে, কারণ গণিত হল স্বতঃসিদ্ধ ভিত্তিক একটি যৌক্তিক ব্যবস্থা।

অতএব, অ্যাম্পিয়ার লুপ উপপাদ্য সবসময় ধরে রাখতে হবে!

যাইহোক, প্রতিভাবান স্কটিশ পদার্থবিদ ম্যাক্সওয়েল আবিষ্কার করেছিলেন যে যখন একটি অস্থির বর্তমান সার্কিটের মুখোমুখি হয়েছিল, তখন অ্যাম্পিয়ার লুপ উপপাদ্যটি পরস্পরবিরোধী ছিল।

ক্যাপাসিটরের চার্জিং এবং ডিসচার্জিংয়ের সময় সাধারণ অস্থির কারেন্ট ঘটে। নীচের চিত্রে দেখানো হয়েছে, ক্যাপাসিটর চার্জ করার স্বল্প সময়ের মধ্যে একটি অস্থির কারেন্ট রয়েছে।

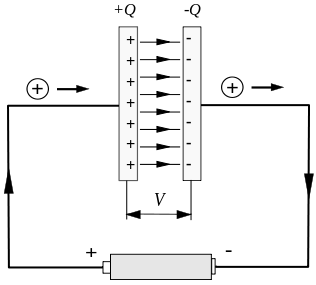
কিন্তু সার্কিট ক্যাপাসিটর প্লেটগুলির মধ্যে সংযোগ বিচ্ছিন্ন করা হয়েছে, যা একটি গুরুতর সমস্যা সৃষ্টি করবে।

ধরুন আমরা একটি বদ্ধ পথ বিবেচনা করি যা তারটিকে বাইপাস করে, যেমনটি নীচের চিত্রে দেখানো হয়েছে, C দ্বারা চিহ্নিত বৃত্ত এবং সীমানা হিসাবে এটির সাথে বাঁকা পৃষ্ঠটি নির্বিচারে নির্বাচন করা যেতে পারে। চিত্রে, C নিজেই এবং ক্যাপাসিটর জুড়ে বৃত্তাকার সমতলটি নির্বাচন করা হয়েছে। বাম প্লেটের বাঁকা পৃষ্ঠ।

বৃত্তাকার পৃষ্ঠ অনুযায়ী, এটি বাঁকা পৃষ্ঠ অনুযায়ী দেখা যায়, কিন্তু চুম্বকীয় ক্ষেত্রের শক্তির একটি লুপ অবিচ্ছেদ্য হিসাবে, এর মান নির্ধারণ করা উচিত!

কিভাবে করবেন?

ম্যাক্সওয়েল বিশ্বাস করেন যে অ্যাম্পিয়ারের লুপ উপপাদ্য অবশ্যই প্রতিষ্ঠিত হবে। এখন যেহেতু একটি সমস্যা আছে, এটি অবশ্যই কারণ স্রোতের একটি অংশ আমাদের দ্বারা আগে আবিষ্কৃত হয়নি, তবে এটি বিদ্যমান!

সুতরাং, বর্তমানের এই অংশটি কীভাবে খুঁজে বের করবেন?

যেহেতু সমস্যাটি প্লেটের মধ্যে, প্লেটের মধ্যে থেকে শুরু করুন।

বিশ্লেষণের মাধ্যমে, ম্যাক্সওয়েল আবিষ্কার করেছেন যে চার্জিং বা ডিসচার্জিং নির্বিশেষে, ক্যাপাসিটর প্লেটের মধ্যে সর্বদা একটি ভৌত ​​পরিমাণ থাকে যা কারেন্টের মাত্রা এবং দিকনির্দেশের সাথে সিঙ্ক্রোনাইজ করা হয়। এটি বৈদ্যুতিক স্থানচ্যুতি ভেক্টরের প্রবাহের সময় ডেরিভেটিভ, অর্থাৎ, এটি স্থানচ্যুতি প্রবাহ হিসাবে সংজ্ঞায়িত করা হয়।

যদি বিবেচনা করা হয় যে এই অংশটি স্রোতের অংশ যা আগে আবিষ্কৃত হয়নি, তাহলে এখন সম্পূর্ণ বর্তমান। অর্থাৎ, যদিও প্লেটগুলির মধ্যে সার্কিট সংযোগ বিচ্ছিন্ন হয়ে গেছে, বৈদ্যুতিক স্থানচ্যুতি প্রবাহের ডেরিভেটিভ এবং কারেন্টের যোগফল, সামগ্রিকভাবে, সর্বদা কারেন্টের ধারাবাহিকতা নিশ্চিত করে।

পূর্ববর্তী দ্বন্দ্বে ফিরে যাওয়া, আমরা এখন জানি যে, স্টোকসের উপপাদ্যের প্রয়োজনীয়তা অনুসারে, একটি বদ্ধ পৃষ্ঠের জন্য তড়িৎ ঘনত্বের প্রবাহ গণনা করার সময়, স্থানচ্যুতি প্রবাহের ঘনত্বকেও বিবেচনা করা উচিত, অর্থাৎ সম্পূর্ণ অ্যাম্পিয়ার লুপ। উপপাদ্য তাই, এই নতুন বর্তমান উপাদান “আবিষ্কার” দ্বারা, অ্যাম্পিয়ার লুপ উপপাদ্যের সংকট সমাধান করা হয়েছে!

কারণ এখানে “পরিচয়” ব্যবহার করা হয়নি, তবে এখানে “আবিষ্কার” ব্যবহার করা হয়েছে। আমি যে বিষয়টিতে জোর দিতে চাই তা হল এই ধরনের স্রোত গাণিতিক ক্ষতিপূরণ নয়, কিন্তু একটি বাস্তব জিনিস, তবে এটি আগে আবিষ্কৃত হয়নি।

কেন এটি প্রথম স্থানে বিদ্যমান? কারণ এটি একটি বৈদ্যুতিক প্রবাহ হিসাবে কাজ করে, একটি পরিবাহী প্রবাহের মতো, এটি একটি চৌম্বক ক্ষেত্রকে সমানভাবে উত্তেজিত করে, বৈদ্যুতিক চার্জের কোন চলাচল নেই, কোন তারের প্রয়োজন হয় না এবং কোন জুল তাপ তৈরি করা যায় না, তাই এটি উপেক্ষা করা হয়েছে!

কিন্তু এটি আসলে নিজেই বিদ্যমান, শুধু একটি লো প্রোফাইল রাখুন, এটি চুম্বক ক্ষেত্র সব সময় নীরবে উত্তেজনাপূর্ণ হয়েছে!

অন্য কথায়, যখন আমরা একটি চৌম্বক ক্ষেত্রের মুখোমুখি হই, তখন বর্তমানের মূল সংজ্ঞাটি খুব সংকীর্ণ। বৈদ্যুতিক প্রবাহের সারাংশ বৈদ্যুতিক চার্জের গতিবিধি নয়, এটি এমন কিছু হওয়া উচিত যা একটি চৌম্বক ক্ষেত্রকে উত্তেজিত করতে পারে।

এ পর্যন্ত, কারেন্টের বিভিন্ন রূপ চালু করা হয়েছে। তারা সব বস্তুনিষ্ঠভাবে বিদ্যমান, এবং তাদের মধ্যে কি মিল রয়েছে তা হল যে সমস্ত স্রোত সমানভাবে চৌম্বক ক্ষেত্রকে উত্তেজিত করতে পারে।