什麼是電流？ 首先回憶一下，我們學過的電流的定義是什麼？

很簡單，帶電粒子在導體中的定向運動是電流。

只有當物質具有可以自由移動的帶電粒子時，它才能傳輸電流，即導電。 這些參與傳導的帶電粒子稱為載流子。 例如，對於金屬，只有原子的外層電子可以作為載流子。

電流定義中的“定向運動”經常被誤解。 很多人認為它是指有一定方向的運動，當然不是！ 交流電路中電子的運動方向不會改變嗎？

其實，定向運動是相對於“隨機運動”而言的！

由於電子是微觀粒子，它們必須一直處於熱運動中。 熱運動是一種隨機運動，如下圖所示。

這個動作其實非常快。 例如，在室溫下的金屬中，電子熱運動的速度在每秒數百公里的數量級！

如果仔細觀察這個隨機運動，你會發現每個粒子的運動方向在任何時刻都是隨機的。 如果將這些粒子的速度矢量相加，結果幾乎為零。

現在給導體加上電場，電子在隨機運動的基礎上疊加定向運動。 假設電場向左移動一段時間，電子的運動如下所示。 紅球代表晶格上的金屬原子，快速移動的點代表自由電子。

它看起來很快嗎？ 那是因為電子運動真的很快！ 但實際上，佔其中很大比例的隨機運動對電流沒有貢獻。 當隨機運動消除後，剩下的就像下面的慢看一樣。

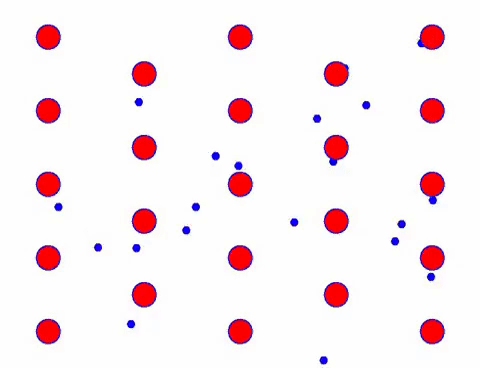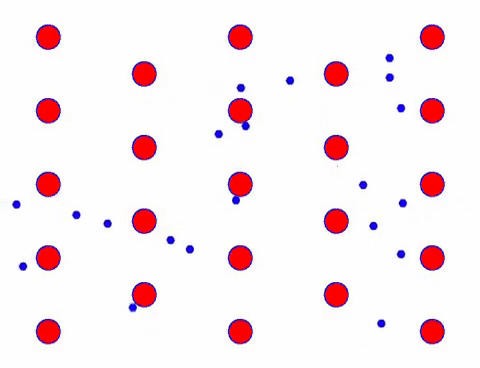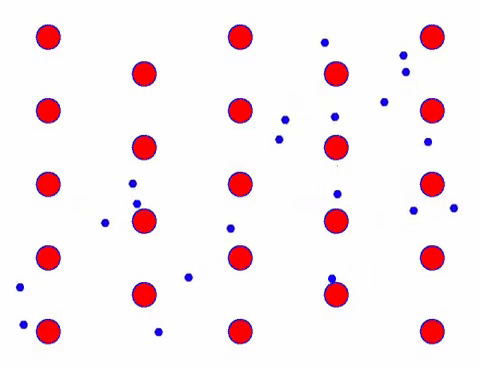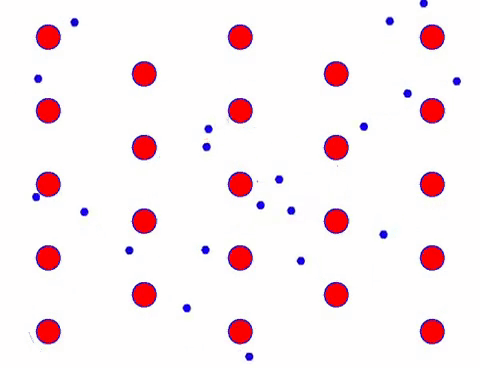
事實上，電子的定向運動比熱運動的速度慢得多。 電子的這種“研磨”運動稱為漂移或“漂移”。 有時，由於與原子的碰撞，電子會朝相反的方向運行。 但一般來說，電子是朝一個方向運動的。

如果電場改變方向，電子漂移的方向也會改變。

因此，這種定向運動意味著在某一時刻參與傳導的所有電子的速度之和不為零，而一般是在某一方向。 這個方向可以隨時改變，交流就是這種情況。

因此，電流與其說是電荷的“定向運動”，不如說是電荷的“集體運動”。

導體中電流的大小用電流強度表示。 電流強度定義為單位時間內通過導體橫截面的電量，即

我們已經學習了一些包含“強度”一詞的物理量，例如電場強度和磁感應強度。 它們一般代表單位時間、單位面積（或單位體積、單位立體角）的比重。 但是，當前強度中的“強度”一詞並不反映該區域的當前分配。

事實上，還有另一個物理量負責電流向面積的分佈，這就是電流密度。

既然電流的本質是電荷的定向運動，那麼電流強度和漂移速度肯定有一定的關係！

為了得到這個關係，首先要明確一個概念——載流子濃度，即單位體積內載流子的數量，用表示。

假設導體截面為，載流子濃度為，漂移速度為，帶電電荷為。

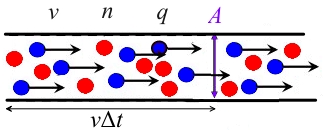
那麼表面左側導體中的電荷為，這些電荷會在一定時間內通過表面，所以

這是電流強度的微觀表達。

電流密度是電流對面積的分配，所以電流密度的大小為金屬可以從這個速度獲得，如下面的例子。

考慮一根銅線，假設每個銅原子貢獻一個電子作為載流子。 有1mol銅，它的體積是，摩爾質量是，密度是，那麼銅線的載流子濃度是

阿伏伽德羅常數在哪裡。 求出銅的密度，代入得到的數值約為單位/立方米。

假設銅線半徑為0.8mm，流過的電流為15A，=1.6C，計算電子漂移速度為

可以看出，電子的漂移速度確實很小。

對於學習電路的人來說，以上就是電流的完整定義。

但在物理學中，上述電流的定義實際上只是一個狹義的定義。 更一般的電流不限於導體，只要電荷的運動是電流。 例如，當氫原子的電子圍繞原子核運動時，在其軌道上形成電流。

假設電荷量為 ，運動週期為 。 那麼每次經過時，都會有如此大量的電荷通過環路的任何截面，因此電流強度是基於週期、頻率和角速度之間的關係，電流也可以表示為

再比如，一個帶電的金屬圓盤，圍繞其軸旋轉，也會形成不同半徑的迴路電流。

這種電流不是正常的傳導電流，不會產生焦耳熱！ 不能形成真正的電路。

不然你給我算一下，氫原子的電子每秒產生多少焦耳熱？

事實上，真空中的電流並不滿足歐姆定律。 因為，對於帶電粒子在真空中運動形成的電流，載流子不會像金屬中的晶格那樣發生碰撞，所以真空沒有電阻，也沒有電導。

電荷的運動產生電流，電荷本身激發電場。 這很容易引起誤解。 因此，許多人認為形成電流的帶電粒子的電場必須暴露。 但實際上，對於一般導體中的傳導電流，載流子是在由大量帶正電的金屬離子組成的背景上流動的，而導體本身是中性的！

我們常稱這種特殊電流為“等效電流”。 這裡的等效是指它產生的磁場與普通傳導電流相同！

提醒：不要將這裡的“等效電流”與電路分析中的“等效電路”混淆

事實上，當我們第一次研究磁場時，比奧-薩法爾定律中的電流就是包含這個等效電流的廣義電流。 當然，麥克斯韋方程組中的傳導電流也指廣義電流。

研究過光電效應的人都知道，當光電子從陰極漂移到陽極時，如果忽略空氣的影響，這個電流是由電荷在真空中的運動引起的，沒有電阻，所以不受歐姆定律限制。

那麼，這是物理學中唯一關於電流的東西嗎？

不！ 也有勵磁電流和位移電流兩種。

它們也是兩個等效的電流，顧名思義，它們也是用來解釋磁性的。 也就是說，他們已經脫離了當前“衝鋒運動”的基本特徵！

太棒了！ 沒有電荷運動，為什麼可以稱為電流呢？

別著急，聽我慢慢說。

我們先來看看磁化電流。

發現磁性是由電的運動引起的（暫不考慮用自旋的內在特性來解釋磁性）。 為了解釋自然磁性，法國物理學家安培提出“分子循環”假說。

如下圖所示，任何一個原子或分子都可以看作是有一個電荷圍繞中心旋轉，形成一個微小的迴路電流，即“分子循環”。

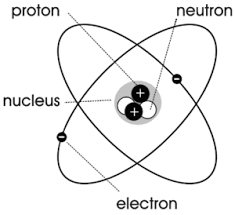
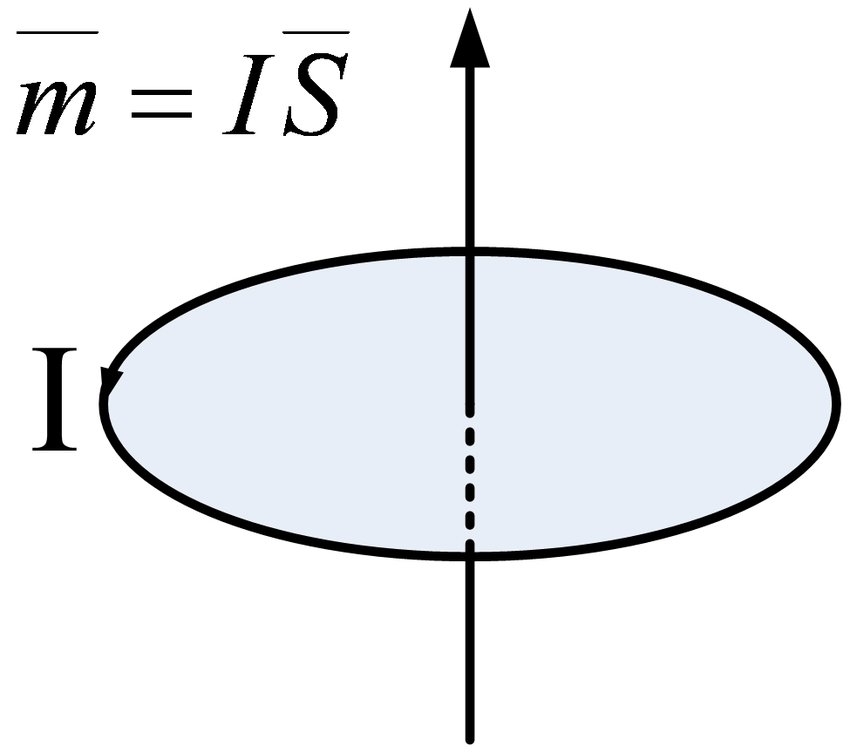
根據電流激發磁場的定律，這種分子循環會產生一個物理量，稱為磁矩。 它的大小是分子環流所圍成的面積乘以分子環流的當量流，其方向與環流方向呈右手螺旋關係，即

顯然，磁矩的方向正好沿著環流形成的磁場方向

.

一般情況下，物質分子循環的排列是混亂的，所以該物質是沒有磁性的，如下圖左側所示。 當受到外磁場作用時，這些分子循環會近似整齊排列。 如下圖右側所示，它們的磁矩盡可能地排列在一個方向，就像無數個小磁針聚集在一起形成一個總磁場，由它們組成的整個材料都具有磁性。

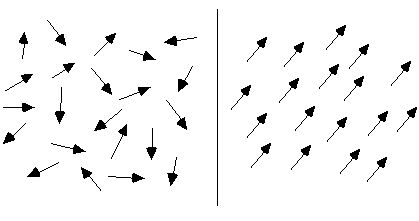
假設有一個圓柱狀的磁鐵，內部分子循環排列整齊，磁鐵段邊緣的每個分子循環段連接在一起，形成一個大循環，如下圖所示。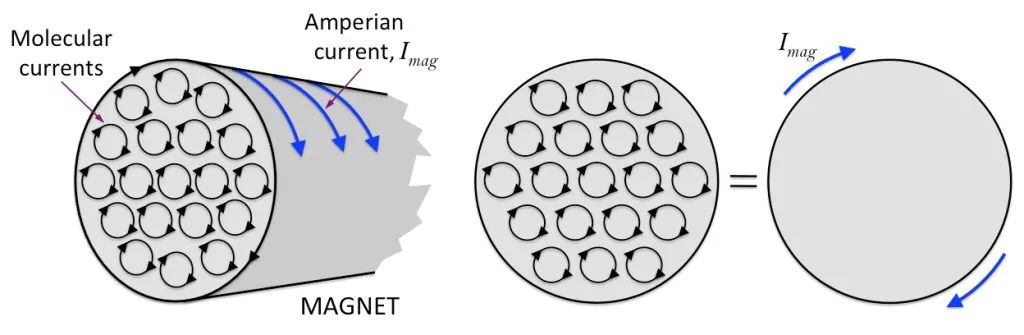

基於此，我們可以認為條形磁鐵就像一個通電的螺線管。 也就是說，有一股無形的電流糾纏在磁鐵的表面！ 這種電流不能接通使用。 它被限制在磁鐵的表面。 我們稱其為“結合電流”或“磁化電流”。

所以磁化電流是電流，因為它和真實電荷運動形成的電流一樣，可以等效地產生磁場！

我們再來看看位移電流。

根據安培環路定理，閉合路徑上磁場強度的積分等於以該路徑為界的任意曲面上的電流密度通量，即該定理在數學上稱為斯托克斯定理。 它告訴我們，向量沿任何閉合路徑的積分必須等於其捲曲（此處）到閉合路徑所限定的任何表面的通量。

既然是數學定理，就一定是正確的，因為數學是建立在公理基礎上的邏輯系統。

因此，安培環定理必須始終成立！

然而，天才的蘇格蘭物理學家麥克斯韋發現，當面對不穩定的電流電路時，安培環定理是矛盾的。

典型的不穩定電流發生在電容器的充電和放電過程中。 如下圖所示，電容器在短時間充電過程中存在不穩定的電流。

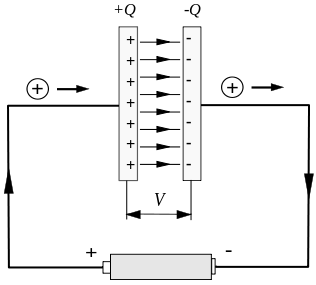
但電路在電容器極板之間斷開，這將導致嚴重的問題。

假設我們考慮一條繞過導線的閉合路徑，如下圖所示，用C標記的圓，以它為邊界的曲面可以任意選擇。 在圖中，選擇了由 C 本身包圍並穿過電容器的圓形平面。 左板的曲面。

根據圓曲面可以看出，根據曲面，但是作為磁場強度的環積分，應該確定它的值！

怎麼做？

麥克斯韋認為安培環定理必須成立。 現在出現問題，一定是因為電流的一部分之前我們沒有發現，但它確實存在！

那麼，如何找出這部分電流呢？

由於問題出在板之間，所以從板之間開始。

通過分析，麥克斯韋發現，無論充電還是放電，電容器極板之間始終存在一個與電流大小和方向同步的物理量。 它是電位移矢量的通量的時間導數，即定義為位移電流。

如果認為這部分是之前未被發現的電流部分，那麼完整的電流就是現在。 也就是說，雖然極板之間的電路是斷開的，但是電位移通量的導數和電流之和，作為一個整體，始終保證了電流的連續性。

回到前面的矛盾，我們現在知道，根據斯托克斯定理的要求，在計算閉合曲面的電流密度通量時，還應考慮位移電流的密度，即完整的安培迴路因此定理是，通過“發現”這個新的電流分量，安培環定理的危機就解決了！

之所以這裡不用“介紹”，而是用“發現”。 我要強調的是，這種電流不是數學補償，而是真實存在的，只是以前沒有發現過。

為什麼它首先存在？ 因為它充當電流，就像傳導電流一樣，它等效地激發了磁場，只是沒有電荷的運動，不需要電線，也不會產生焦耳熱，所以一直被忽略！

但它其實是自己存在的，只是低調一點，它一直在默默地激發著那裡的磁場！

換句話說，當我們面對磁場時，電流的原始定義太狹窄了。 電流的本質不是電荷的運動，它應該是能激發磁場的東西。

到目前為止，已經介紹了幾種形式的電流。 它們都是客觀存在的，它們的共同點是所有的電流都能同等地激發磁場。