Vad är den elektriska strömmen? Första minns, vad är definitionen av ström som vi har lärt oss?

Helt enkelt är den riktade rörelsen av laddade partiklar i en ledare en elektrisk ström.

Först när ett ämne har laddade partiklar som kan röra sig fritt kan det överföra elektrisk ström – det vill säga leda elektricitet. Dessa laddade partiklar som deltar i ledning kallas bärare. För metaller, till exempel, kan bara de yttre elektronerna hos atomer fungera som bärare.

Den “riktade rörelsen” i definitionen av elektrisk ström missförstås ofta. Många tror att det syftar på rörelse med en viss riktning, naturligtvis inte! Förändras inte rörelseriktningen för elektronerna i AC-kretsen?

Faktum är att orientering är relativt till “slumpmässig rörelse”!

Eftersom elektroner är mikroskopiska partiklar måste de vara i termisk rörelse hela tiden. Termisk rörelse är en slumpmässig rörelse, som visas i figuren nedan.

Denna rörelse är faktiskt väldigt snabb. Till exempel, i metaller vid rumstemperatur är hastigheten för elektronisk termisk rörelse i storleksordningen hundratals kilometer per sekund!

Om du tittar noga på denna slumpmässiga rörelse, kommer du att upptäcka att rörelseriktningen för varje partikel är slumpmässig när som helst. Om du lägger ihop hastighetsvektorerna för dessa partiklar blir resultatet nästan noll.

Lägg nu till ett elektriskt fält till ledaren, och elektronen överlagrar en riktningsrörelse på basis av slumpmässig rörelse. Om man antar att det elektriska fältet är till vänster under en viss tid ser elektronernas rörelse ut som följande. De röda kulorna representerar metallatomer på kristallgittret, och de snabbt rörliga prickarna representerar fria elektroner.

Ser det snabbt ut? Det beror på att elektronisk rörelse är riktigt snabb! Men i själva verket bidrar inte den slumpmässiga rörelsen, som står för en stor del av den, till strömmen. När den slumpmässiga rörelsen är eliminerad, är resten precis som den långsamma looken nedan.

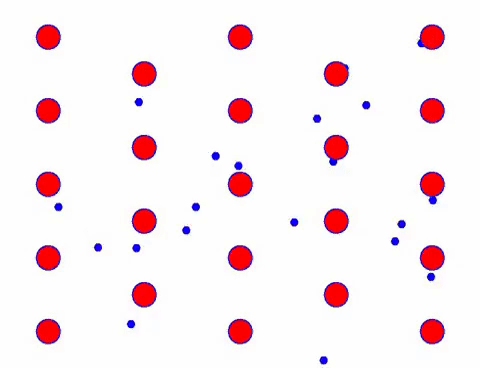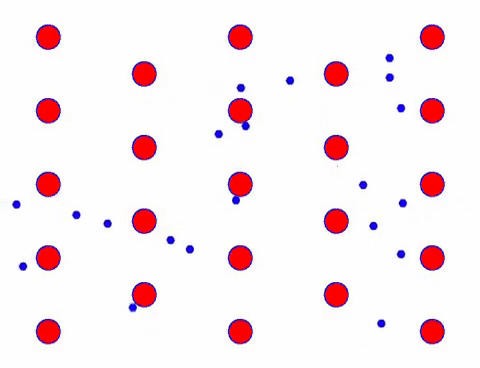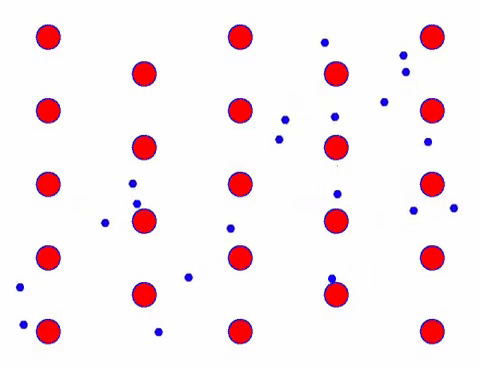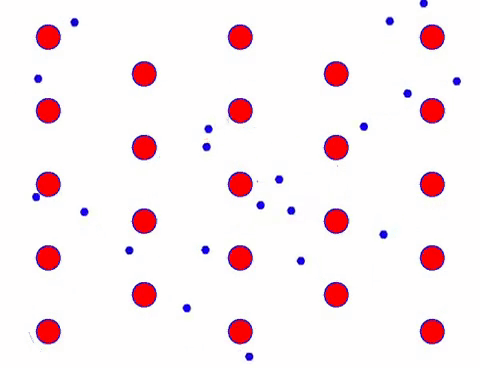
Faktum är att elektronernas riktningsrörelse är mycket långsammare än hastigheten för termisk rörelse. Denna “malande” rörelse av elektroner kallas drift eller “drift”. Ibland kommer elektroner att springa i motsatt riktning på grund av kollisioner med atomer. Men i allmänhet rör sig elektroner i en riktning.

Om det elektriska fältet ändrar riktning kommer även elektrondriftens riktning att ändras.

Därför innebär denna typ av riktningsrörelse att summan av hastigheterna för alla elektroner som deltar i ledningen vid en viss tidpunkt inte är noll, utan är generellt i en viss riktning. Denna riktning kan ändras när som helst, och det är fallet med växelström.

Därför är ström inte så mycket den “riktade rörelsen” av elektrisk laddning som den är den “kollektiva rörelsen” av elektrisk laddning.

Storleken på strömmen i ledaren uttrycks av strömstyrkan. Strömintensiteten definieras som mängden elektricitet som passerar genom ledarens tvärsnitt under en tidsenhet, nämligen

Vi har lärt oss några fysikaliska storheter som innehåller ordet “intensitet”, såsom elektriska fältintensitet och magnetisk induktionsintensitet. De representerar i allmänhet fördelningen per tidsenhet, enhetsarea (eller enhetsvolym, enhet rymdvinkel). Ordet ”intensitet” i den aktuella intensiteten återspeglar dock inte den aktuella fördelningen av området.

Faktum är att en annan fysisk storhet är ansvarig för fördelningen av ström till området, vilket är strömtätheten.

Eftersom kärnan i elektrisk ström är den elektriska laddningens riktningsrörelse måste det finnas ett visst samband mellan strömintensitet och drifthastighet!

För att få fram detta förhållande måste vi först klargöra en begreppsbärarkoncentration, det vill säga antalet bärare i en volymenhet, vilket uttrycks med .

Det antas att ledartvärsnittet är, bärarkoncentrationen är, drifthastigheten är och den laddade laddningen är.

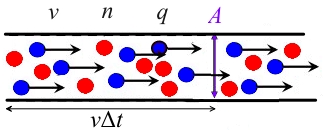
Då är laddningen i ledaren på ytans vänstra sida, och dessa laddningar kommer att passera genom ytan inom en viss tidsperiod, så

Detta är ett mikroskopiskt uttryck för strömintensitet.

Strömtäthet är fördelningen av ström till area, så storleken på strömtätheten är, men den definieras som en vektor, och riktningen är riktningen för avdriftshastighetsvektorn för de positivt laddade bärarna, så avdriften av elektroner i metall kan erhållas från denna hastighet, som ett exempel nedan.

Betrakta en koppartråd, förutsatt att varje kopparatom bidrar med en elektron som bärare. Det finns 1 mol koppar, dess volym är, molmassan är, densiteten är, då är bärarkoncentrationen av koppartråden

Var är Avogadros konstant. Densiteten av koppar hittas, och värdet som erhålls genom att ersätta är ungefär enhet/kubikmeter.

Om man antar att koppartrådens radie är 0.8 mm, är strömmen 15A, =1.6 C, och elektronernas drifthastighet beräknas som

Det kan ses att avdriftshastigheten för elektroner verkligen är mycket liten.

För den som studerar kretsar är ovanstående den fullständiga definitionen av ström.

Men inom fysiken är ovanstående definition av ström faktiskt bara en snäv definition. Mer allmänna strömmar är inte begränsade till ledare, så länge som rörelsen av elektriska laddningar är ström. Till exempel, när elektronerna i en väteatom rör sig runt kärnan, bildas en elektrisk ström i dess omloppsbana.

Antag att mängden elektronisk laddning är och rörelseperioden är. Sedan varje gång det går passerar en så stor mängd laddning genom valfritt tvärsnitt av slingan, så strömintensiteten baseras på förhållandet mellan period, frekvens och vinkelhastighet, och strömmen kan också uttryckas som

Till ett annat exempel, en laddad metallskiva, som roterar runt sin axel, bildar också slingströmmar med olika radier.

Denna typ av ström är inte en normal ledningsström och kan inte generera Joule-värme! Kan inte bilda en riktig krets.

Annars, skulle du ge mig en beräkning av hur mycket joule-värme som genereras per sekund av väteatomens elektroner?

Faktum är att strömmen i vakuum inte uppfyller Ohms lag. Eftersom, för den elektriska ström som bildas av rörelsen av laddade partiklar i vakuumet, kolliderar inte bärarna på samma sätt som gallret i metallen, så vakuumet har inget motstånd och ingen konduktans.

Rörelsen av elektriska laddningar genererar elektrisk ström, och den elektriska laddningen i sig exciterar det elektriska fältet. Detta är lätt att orsaka ett missförstånd. Många tror därför att det elektriska fältet hos de laddade partiklar som bildar den elektriska strömmen måste exponeras. Men i själva verket, för ledningsströmmen i en allmän ledare, flyter bärare på en bakgrund som består av ett stort antal positivt laddade metalljoner, och själva ledaren är neutral!

Vi kallar ofta denna typ av specialström för en “ekvivalent ström”. Motsvarigheten här betyder att den genererar ett magnetfält på samma grund som en vanlig ledningsström!

Påminnelse: Blanda inte ihop “ekvivalent ström” här med “ekvivalent krets” i kretsanalys

Faktum är att när vi först studerade magnetfältet var den elektriska strömmen i Biot-Saffars lag den generaliserade elektriska ström som innehöll denna ekvivalenta ström. Självklart hänvisar ledningsströmmen i Maxwells ekvationer också till den generaliserade strömmen.

De som har studerat den fotoelektriska effekten vet att när fotoelektronen driver från katoden till anoden, om luftens inverkan ignoreras, orsakas denna ström av rörelsen av elektriska laddningar i vakuumet, och det finns inget motstånd, så det är inte begränsad av Ohms lag.

Så, är detta det enda med elektrisk ström i fysiken?

Nej! Det finns också två typer, nämligen magnetiseringsström och förskjutningsström.

De är också två ekvivalenta strömmar, som, som namnet antyder, också introduceras för att förklara magnetism. De har med andra ord brutit sig loss från den grundläggande egenskapen hos den nuvarande ”laddningsrörelsen”!

Det är fantastiskt! Det finns ingen elektrisk laddningsrörelse, så varför kan det kallas en elektrisk ström?

Oroa dig inte, och lyssna långsamt på mig.

Låt oss först titta på magnetiseringsströmmen.

Man fann att magnetism orsakas av elektricitets rörelse (för tillfället utan hänsyn till förklaringen av magnetism av spinns inneboende egenskaper). För att förklara naturlig magnetism lade den franske fysikern Ampere fram hypotesen om “molekylär cirkulation”.

Som visas i figuren nedan kan varje atom eller molekyl anses ha en elektrisk laddning som roterar runt mitten och bildar en liten slingström, det vill säga “molekylär cirkulation”.

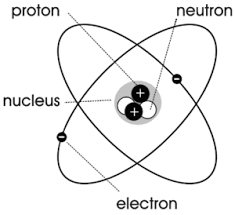
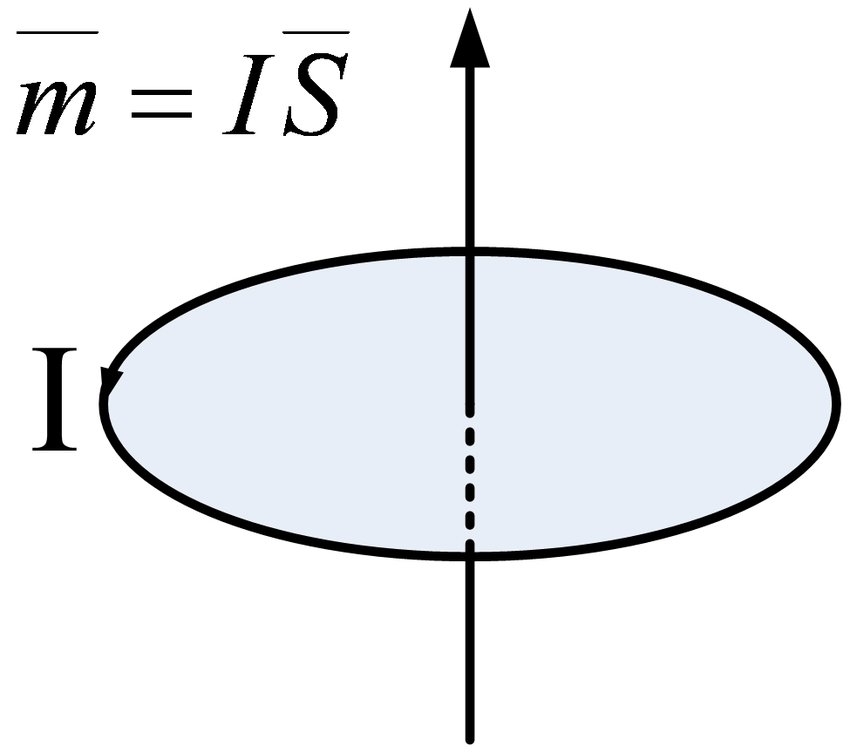
Enligt lagen att den elektriska strömmen exciterar magnetfältet kommer denna molekylära cirkulation att producera en fysisk storhet som kallas magnetiskt moment. Dess storlek är det område som omges av molekylcirkulationen multiplicerat med molekylcirkulationens ekvivalenta ström, och dess riktning är i ett högerhänt spiralförhållande med cirkulationens riktning, dvs.

Uppenbarligen är riktningen för det magnetiska momentet exakt längs riktningen för det magnetiska fältet som bildas av den cirkulerande strömmen

.

Under normala omständigheter är arrangemanget av ett ämnes molekylära cirkulation kaotisk, så ämnet är inte magnetiskt, som visas på vänster sida av figuren nedan. När de utsätts för ett externt magnetfält kommer dessa molekylära cirkulationer att vara ungefär prydligt arrangerade. Som visas på höger sida av figuren nedan är deras magnetiska moment så mycket som möjligt ordnade i en riktning, precis som otaliga små magnetiska nålar som samlas ihop för att bilda ett totalt magnetfält, och hela materialet som består av dem blir magnetiskt.

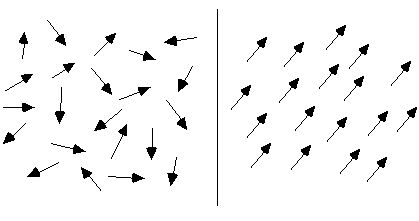
Antag att det finns en cylindrisk magnet, den inre molekylära cirkulationen är snyggt arrangerad och sektionerna av varje molekylär cirkulation vid kanten av magnetsektionen är sammankopplade för att bilda en stor cirkulation, som visas i figuren nedan.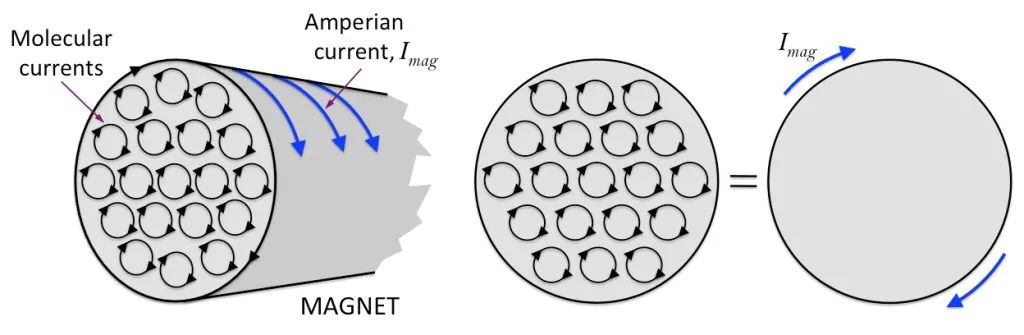

Baserat på detta kan vi tro att en stångmagnet är som en magnetiserad solenoid. Det finns med andra ord en osynlig ström intrasslad på magnetens yta! Denna typ av ström kan inte anslutas och användas. Den är begränsad till magnetens yta. Vi kallar det “bindande ström” eller “magnetiseringsström”.

Därför är magnetiseringsströmmen en ström, eftersom den är densamma som den ström som bildas av rörelsen av verkliga elektriska laddningar, som på motsvarande sätt kan generera ett magnetfält!

Låt oss titta på förskjutningsströmmen igen.

Enligt Amperes loopsats är integralen av magnetfältstyrkan på en sluten bana lika med flödet av strömtätheten på vilken krökt yta som helst som begränsas av denna bana, det vill säga denna sats kallas Stokes sats i matematik. Det säger oss att integralen av en vektor längs en stängd bana måste vara lika med flödet av dess krullning (här) till vilken yta som helst som begränsas av den stängda banan.

Eftersom det är ett matematiskt teorem måste det alltid vara korrekt, eftersom matematik är ett logiskt system baserat på axiom.

Därför måste Ampere Loop Theorem alltid hålla!

Den begåvade skotske fysikern Maxwell upptäckte dock att när den stod inför en instabil strömkrets var Amperes loopsats motsägelsefull.

Den typiska instabila strömmen uppstår under laddning och urladdning av kondensatorn. Som visas i figuren nedan finns det en instabil ström under den korta perioden av kondensatorladdning.

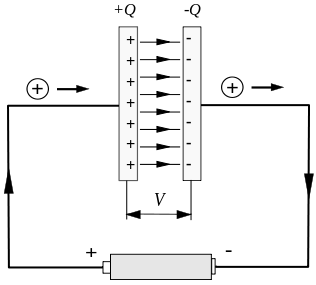
Men kretsen är frånkopplad mellan kondensatorplattorna, vilket kommer att orsaka ett allvarligt problem.

Antag att vi betraktar en stängd bana som går förbi tråden, som visas i figuren nedan, cirkeln markerad med C och den krökta ytan med den som gräns kan väljas godtyckligt. I figuren är det cirkulära planet omslutet av C själv och över kondensatorn valt. Den böjda ytan på den vänstra plattan.

Enligt den cirkulära ytan kan man se att enligt den krökta ytan, men som en slingintegral av magnetfältets styrka, bör dess värde bestämmas!

Hur göra?

Maxwell anser att Amperes loopsats måste fastställas. Nu när det finns ett problem måste det bero på att en del av strömmen inte har upptäckts av oss tidigare, men den finns!

Så, hur får man reda på den här delen av strömmen?

Eftersom problemet är mellan plattorna, utgå från mellan plattorna.

Genom analys fann Maxwell att oavsett laddning eller urladdning finns det en fysisk storhet mellan kondensatorplattorna hela tiden som är synkroniserad med strömmens storlek och riktning. Det är tidsderivatan av flödet av den elektriska förskjutningsvektorn, det vill säga den definieras som förskjutningsströmmen.

Om man anser att denna del är den del av strömmen som inte har upptäckts tidigare, så är den fullständiga strömmen nu. Det vill säga, även om kretsen mellan plattorna är frånkopplad, säkerställer derivatan av det elektriska förskjutningsflödet och summan av strömmen tillsammans, som helhet , strömmens kontinuitet hela tiden.

Om vi ​​går tillbaka till den tidigare motsägelsen, så vet vi nu att, enligt kraven i Stokes sats, vid beräkning av strömtäthetsflödet för en sluten yta, bör densiteten för förskjutningsströmmen också beaktas, det vill säga hela ampereslingan Teorem är därför, Genom att “upptäcka” denna nya nuvarande komponent, är krisen med Ampere Loop Theorem löst!

Anledningen till att ”introduktion” inte används här, utan ”upptäckt” används här. Det jag vill betona är att den här typen av ström inte är en matematisk kompensation, utan en riktig sak, men den har inte upptäckts tidigare.

Varför finns det i första hand? Eftersom den fungerar som en elektrisk ström, som en ledningsström, exciterar den ett magnetiskt fält på motsvarande sätt, förutom att det inte finns någon rörelse av elektriska laddningar, ingen tråd krävs och ingen Joule-värme kan genereras, så det har ignorerats!

Men det finns faktiskt av sig självt, håll bara låg profil, det har i tysthet varit spännande med magnetfältet där hela tiden!

Med andra ord, när vi står inför ett magnetfält är den ursprungliga definitionen av ström för snäv. Kärnan i elektrisk ström är inte rörelsen av elektrisk laddning, det borde vara något som kan excitera ett magnetfält.

Hittills har de olika formerna av ström introducerats. De existerar alla objektivt, och vad de har gemensamt är att alla strömmar kan excitera magnetfältet lika mycket.