電流は何ですか？ 最初に思い出してください、私たちが学んだ電流の定義は何ですか？

非常に簡単に言えば、導体内の荷電粒子の方向性のある動きは電流です。

Only when a substance has charged particles that can move freely, it can transmit electric current—that is, conduct electricity. These charged particles that participate in conduction are called carriers. For metals, for example, only the outer electrons of atoms can act as carriers.

The “directional movement” in the definition of electric current is often misunderstood. Many people think it refers to movement with a certain direction, of course not! Doesn’t the direction of movement of the electrons in the AC circuit change?

実際、オリエンテーリングは「ランダムな動き」に関連しています。

電子は微視的な粒子であるため、常に熱運動している必要があります。 下の図に示すように、熱運動はランダムな運動です。

This movement is actually very fast. For example, in metals at room temperature, the speed of electronic thermal movement is on the order of hundreds of kilometers per second!

If you look closely at this random movement, you will find that the direction of movement of each particle is random at any moment. If you add up the velocity vectors of these particles, the result is almost zero.

Now add an electric field to the conductor, and the electron superimposes a directional movement on the basis of random movement. Assuming that the electric field is to the left for a certain period of time, the movement of the electrons looks like the following. The red balls represent metal atoms on the crystal lattice, and the fast moving dots represent free electrons.

速く見えますか？ それは、電子的な動きが本当に速いからです！ しかし実際には、その大部分を占めるランダムな動きは、電流に寄与しません。 ランダムな動きがなくなると、残りは下のスロールックのようになります。

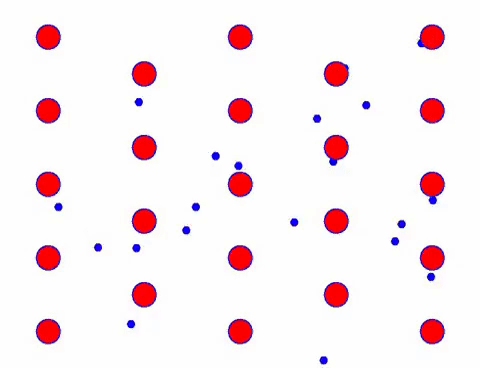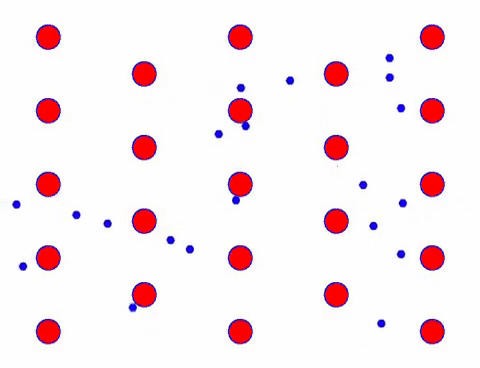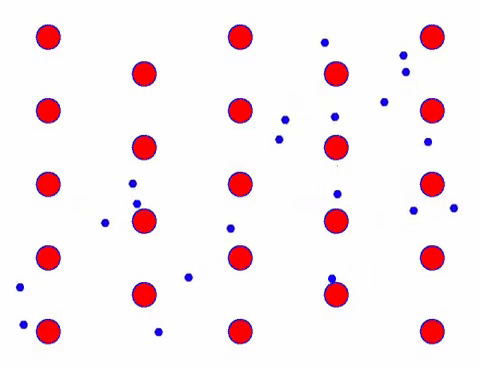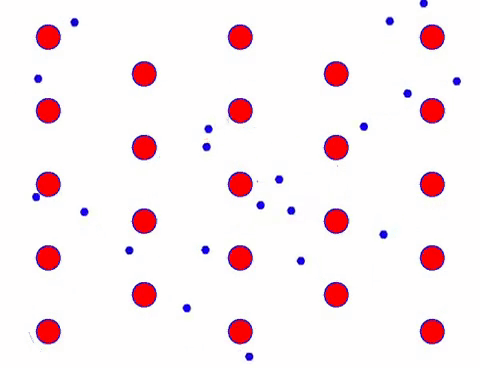
確かに、電子の方向性のある動きは、熱の動きの速度よりもはるかに遅いです。 この電子の「粉砕」運動は、ドリフトまたは「ドリフト」と呼ばれます。 原子との衝突により、電子が反対方向に走る場合があります。 しかし、一般的に、電子は一方向に移動します。

If the electric field changes direction, the direction of electron drift will also change.

したがって、この種の方向性のある動きは、特定の時間に伝導に関与するすべての電子の速度の合計がゼロではなく、一般的に特定の方向にあることを意味します。 この方向はいつでも変更できます。これは交流の場合です。

したがって、電流は電荷の「集合的な動き」ではなく、電荷の「方向性のある動き」ではありません。

The magnitude of the current in the conductor is expressed by the current intensity. The current intensity is defined as the amount of electricity passing through the cross-section of the conductor in a unit time, namely

電界強度や磁気誘導強度など、「強度」という言葉を含むいくつかの物理量を学びました。 これらは通常、単位時間、単位面積（または単位体積、単位立体角）あたりの配分を表します。 ただし、現在の強度の「強度」という言葉は、その領域の現在の配分を反映していません。

実際、別の物理量が、電流密度である面積への電流の分布に関与しています。

Since the essence of electric current is the directional movement of electric charge, there must be a certain relationship between current intensity and drift speed!

In order to obtain this relationship, we must first clarify a concept-carrier concentration, that is, the number of carriers in a unit volume, which is expressed by .

導体断面積は、キャリア濃度は、ドリフト速度は、帯電電荷はであると仮定します。

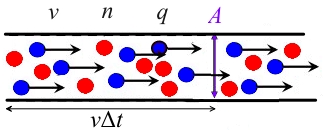
すると、表面左側の導体の電荷はであり、これらの電荷は一定時間内に表面を通過するので、

This is a microscopic expression of current intensity.

Current density is the apportionment of current to area, so the magnitude of current density is, but it is defined as a vector, and the direction is the direction of the drift velocity vector of the positively charged carriers, so the drift of electrons in the metal can be obtained from this Speed, as an example below.

各銅原子がキャリアとして電子に寄与すると仮定して、銅線を考えます。 銅は1molあり、その体積は、モル質量は、密度は、銅線のキャリア濃度は次のようになります。

アボガドロ定数はどこにありますか。 銅の密度がわかり、代入して得られる値は約単位/立方メートルです。

銅線の半径を0.8mmとすると、流れる電流は15A、= 1.6Cとなり、電子のドリフト速度は次のように計算されます。

電子のドリフト速度は確かに非常に小さいことがわかります。

回路を研究する人にとって、上記は電流の完全な定義です。

But in physics, the above definition of current is actually only a narrow definition. More general currents are not limited to conductors, as long as the movement of electric charges is current. For example, when the electrons of a hydrogen atom move around the nucleus, an electric current is formed in its orbit.

Suppose the amount of electronic charge is and the period of movement is. Then every time that elapses, there is such a large amount of charge passing through any cross section of the loop, so the current intensity is based on the relationship between period, frequency and angular velocity, and the current can also be expressed as

別の例では、その軸を中心に回転する帯電した金属ディスクも、異なる半径のループ電流を形成します。

この種の電流は通常の伝導電流ではなく、ジュール熱を発生させることはできません。 実際の回路を形成することはできません。

それ以外の場合、水素原子の電子によってXNUMX秒間に生成されるジュール熱の計算を教えてください。

In fact, the current in vacuum does not satisfy Ohm’s law. Because, for the electric current formed by the movement of charged particles in the vacuum, the carriers are not collided similar to the lattice in the metal, so the vacuum has no resistance and no conductance.

電荷の動きによって電流が発生し、電荷自体が電界を励起します。 これは誤解を招きやすいです。 したがって、多くの人々は、電流を形成する荷電粒子の電界を露出させる必要があると考えています。 しかし実際には、一般的な導体の伝導電流の場合、キャリアは多数の正に帯電した金属イオンで構成されるバックグラウンドを流れ、導体自体は中性です。

We often call this kind of special current an “equivalent current”. The equivalent here means that it generates a magnetic field on the same basis as an ordinary conduction current!

Reminder: Do not confuse the “equivalent current” here with the “equivalent circuit” in circuit analysis

実際、私たちが最初に磁場を研究したとき、Biot-Saffarの法則における電流は、この等価電流を含む一般化された電流でした。 もちろん、マクスウェルの方程式の伝導電流は一般化された電流も指します。

光電効果を研究した人は、光電子が陰極から陽極にドリフトするとき、空気の影響を無視すると、この電流は真空中の電荷の動きによって引き起こされ、抵抗がないことを知っています。オームの法則によって制限されていません。

それで、これは物理学における電流についての唯一のことですか？

No! There are also two types, namely magnetizing current and displacement current.

それらはまた、名前が示すように、磁気を説明するために導入されたXNUMXつの同等の電流です。 つまり、現在の「チャージムーブメント」の基本的な特徴から脱却しました！

すごい！ 電荷の動きがないのに、なぜ電流と呼べるのか。

心配しないで、ゆっくり聞いてください。

まず、磁化電流を見てみましょう。

磁性は電気の動きによって引き起こされることがわかった（当面はスピンの固有の性質による磁性の説明は考慮しない）。 フランスの物理学者アンペアは、自然の磁性を説明するために、「分子循環」の仮説を提唱しました。

As shown in the figure below, any atom or molecule can be regarded as having an electric charge rotating around the center, forming a tiny loop current, that is, “molecular circulation”.

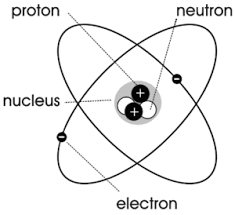
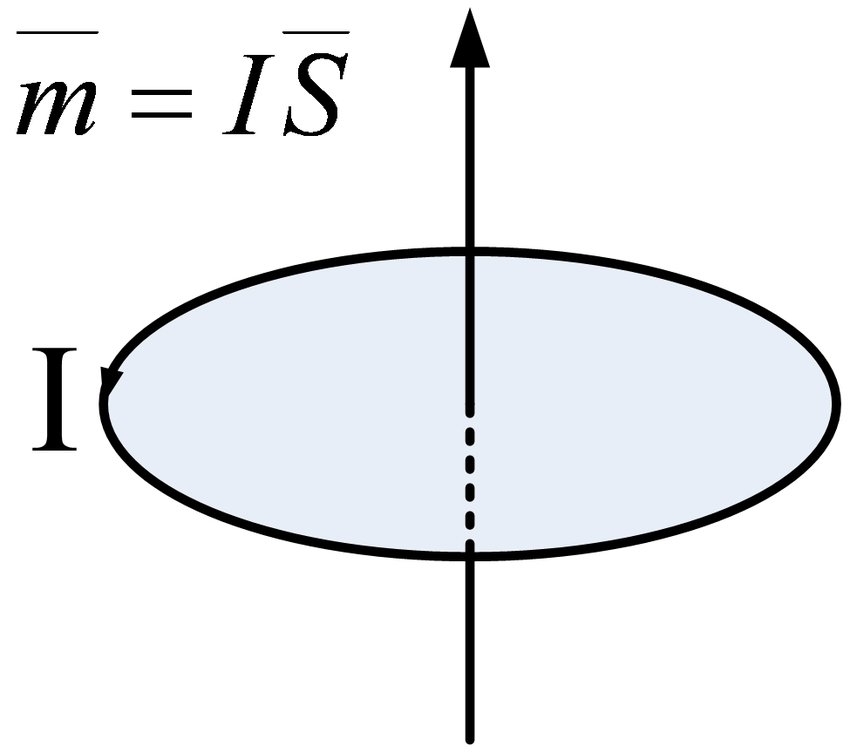
According to the law that the electric current excites the magnetic field, this molecular circulation will produce a physical quantity called magnetic moment. Its size is the area enclosed by the molecular circulation multiplied by the equivalent current of the molecular circulation, and its direction is in a right-handed spiral relationship with the direction of the circulation, namely

明らかに、磁気モーメントの方向は、循環電流によって形成される磁場の方向に正確に沿っています。

.

下の図の左側に示すように、通常の状況では、物質の分子循環の配置は無秩序であるため、物質は磁性を帯びていません。 外部磁場にさらされると、これらの分子循環はほぼきれいに配置されます。 下の図の右側に示すように、それらの磁気モーメントは、無数の小さな磁気針が集まって全磁場を形成するように、可能な限り一方向に配置され、それらで構成される材料全体が磁気になります。

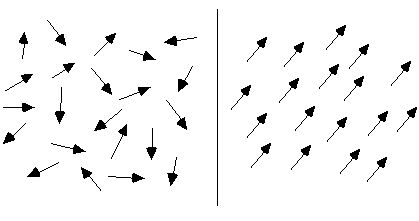
下図のように、円筒形の磁石があり、内部の分子循環がきちんと配置されており、磁石部分の端にある各分子循環の部分がつながって大きな循環を形成しているとします。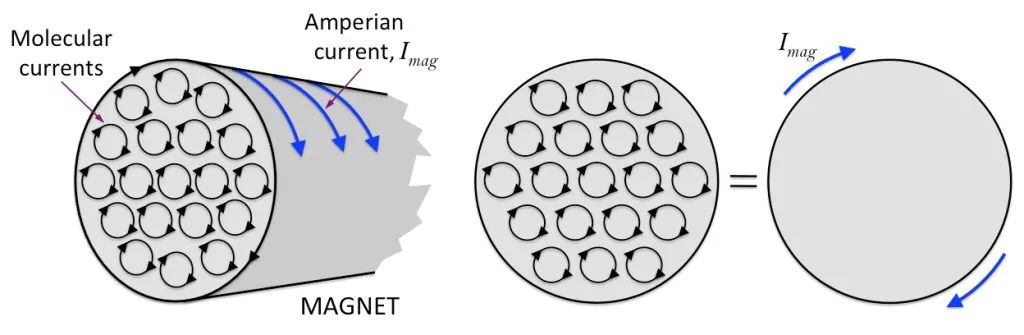

これに基づいて、棒磁石は通電されたソレノイドのようなものであると考えることができます。 つまり、磁石の表面に目に見えない電流が絡み合っているのです！ この種の電流は接続して使用することはできません。 それは磁石の表面に閉じ込められています。 これを「結合電流」または「磁化電流」と呼びます。

Therefore, the magnetizing current is a current, because it is the same as the current formed by the movement of real electric charges, which can equivalently generate a magnetic field!

変位電流をもう一度見てみましょう。

アンペアのループ定理によれば、閉じた経路での磁場の強さの積分は、この経路で囲まれた曲面上の電流密度の磁束に等しくなります。つまり、この定理は数学ではストークスの定理と呼ばれます。 これは、閉じたパスに沿ったベクトルの積分は、閉じたパスで囲まれた任意のサーフェスへのそのカール（ここでは）の流束に等しくなければならないことを示しています。

数学は公理に基づく論理システムであるため、これは数学の定理であるため、常に正しくなければなりません。

したがって、アンペアループの定理は常に成り立つ必要があります！

しかし、才能のあるスコットランドの物理学者マクスウェルは、不安定な電流回路に直面したとき、アンペアループの定理が矛盾していることを発見しました。

The typical unstable current occurs during the charging and discharging of the capacitor. As shown in the figure below, there is an unstable current during the short period of capacitor charging.

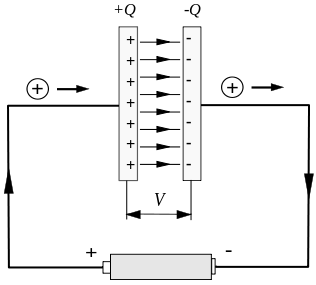
But the circuit is disconnected between the capacitor plates, which will cause a serious problem.

次の図に示すように、ワイヤをバイパスする閉じたパス、Cでマークされた円、およびそれを境界とする曲面を任意に選択できると仮定します。 この図では、C自体で囲まれ、コンデンサの両端にある円形平面が選択されています。 左プレートの曲面。

円形の表面によると、曲面によるとわかりますが、磁場の強さのループ積分として、その値を決定する必要があります！

実行する方法？

マクスウェルは、アンペアのループ定理を確立する必要があると考えています。 問題が発生したのは、これまで電流の一部が発見されていなかったためと思われますが、存在しているのです！

So, how to find out this part of the current?

問題はプレート間であるため、プレート間から開始します。

Through analysis, Maxwell found that regardless of charging or discharging, there is a physical quantity between the capacitor plates at all times that is synchronized with the magnitude and direction of the current. It is the time derivative of the flux of the electric displacement vector, that is, it is defined as the displacement current.

この部分がこれまで発見されていなかった電流の一部であると考えられる場合、完全な電流は現在です。 つまり、プレート間の回路は切断されていますが、電気変位磁束の導関数と電流の合計が全体として、常に電流の連続性を確保します。

Going back to the previous contradiction, we now know that, according to the requirements of Stokes’ theorem, when calculating the flux of current density for a closed surface, the density of displacement current should also be considered, that is, the complete ampere loop theorem is therefore, By “discovering” this new current component, the crisis of the Ampere Loop Theorem is resolved!

The reason why “introduction” is not used here, but “discovery” is used here. What I want to emphasize is that this kind of current is not a mathematical compensation, but a real thing, but it has not been discovered before.

そもそもなぜ存在するのですか？ 伝導電流のように電流として作用するため、電荷の移動がなく、配線が不要で、ジュール熱が発生しないことを除けば、同等に磁場を励起するため、無視されています。

しかし、それは実際にはそれ自体で存在し、目立たないようにしてください。それはずっと静かに磁場を刺激してきました！

In other words, when we face a magnetic field, the original definition of current is too narrow. The essence of electric current is not the movement of electric charge, it should be something that can excite a magnetic field.

これまでに、いくつかの形式の電流が導入されてきました。 それらはすべて客観的に存在し、それらに共通しているのは、すべての電流が磁場を等しく励起できるということです。