विद्युत प्रवाह के हो? पहिले सम्झनुहोस्, हामीले सिकेका वर्तमानको परिभाषा के हो?

एकदम सरल रूपमा, कन्डक्टरमा चार्ज गरिएका कणहरूको दिशात्मक आन्दोलन एक विद्युतीय प्रवाह हो।

जब कुनै पदार्थले स्वतन्त्र रूपमा चल्न सक्ने कणहरू चार्ज गरेको हुन्छ, तब मात्र यसले विद्युतीय प्रवाह – अर्थात्, बिजुली सञ्चालन गर्न सक्छ। चालनमा भाग लिने यी चार्ज गरिएका कणहरूलाई वाहक भनिन्छ। धातुहरूको लागि, उदाहरणका लागि, केवल परमाणुहरूको बाहिरी इलेक्ट्रोनहरूले वाहकको रूपमा काम गर्न सक्छन्।

विद्युतीय प्रवाह को परिभाषा मा “दिशात्मक आन्दोलन” अक्सर गलत बुझिन्छ। धेरै मानिसहरू सोच्छन् कि यसले एक निश्चित दिशाको साथ आन्दोलनलाई जनाउँछ, पक्कै होइन! के AC सर्किटमा इलेक्ट्रोनहरूको चालको दिशा परिवर्तन हुँदैन?

वास्तवमा, अभिमुखीकरण “यादृच्छिक आन्दोलन” को सापेक्ष हो!

इलेक्ट्रोनहरू माइक्रोस्कोपिक कणहरू हुनाले, तिनीहरू सबै समय थर्मल गतिमा हुनुपर्छ। थर्मल गति एक अनियमित गति हो, जस्तै तलको चित्रमा देखाइएको छ।

यो आन्दोलन वास्तवमा धेरै छिटो छ। उदाहरणका लागि, कोठाको तापक्रममा धातुहरूमा, इलेक्ट्रोनिक थर्मल आन्दोलनको गति सयौं किलोमिटर प्रति सेकेन्डको क्रममा हुन्छ!

यदि तपाईंले यस अनियमित आन्दोलनलाई नजिकबाट हेर्नुभयो भने, तपाईंले पाउनुहुनेछ कि प्रत्येक कणको चालको दिशा कुनै पनि क्षणमा अनियमित हुन्छ। यदि तपाइँ यी कणहरूको वेग वेक्टरहरू जोड्नुहुन्छ भने, परिणाम लगभग शून्य हुन्छ।

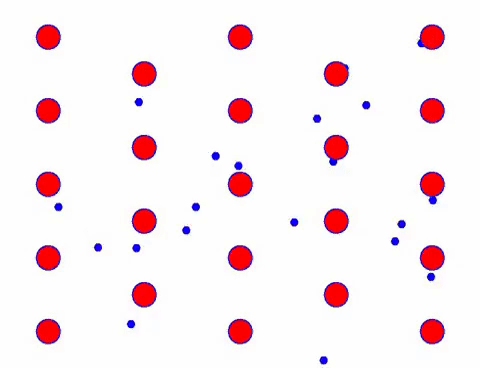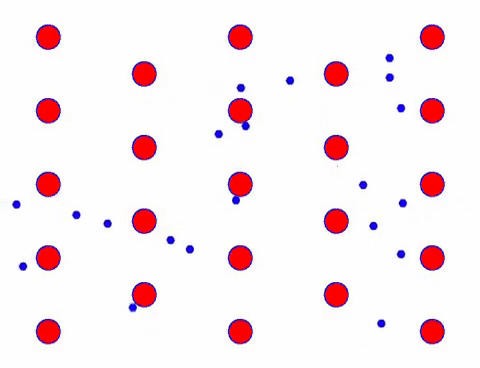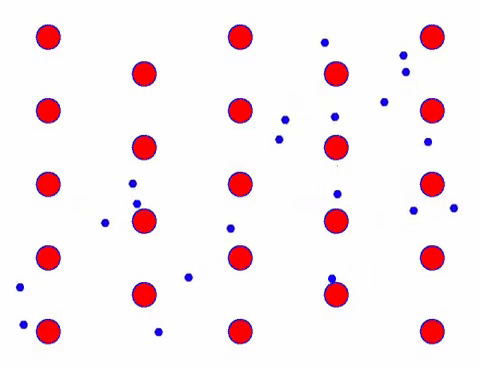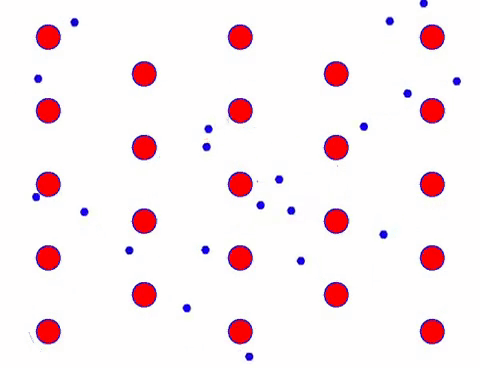
अब कन्डक्टरमा विद्युतीय क्षेत्र थप्नुहोस्, र इलेक्ट्रोनले अनियमित आन्दोलनको आधारमा दिशात्मक आन्दोलनलाई सुपरइम्पोज गर्दछ। विद्युतीय क्षेत्र निश्चित समयको लागि बाँया तर्फ रहेको मानेर, इलेक्ट्रोनहरूको चाल निम्न जस्तो देखिन्छ। रातो बलहरूले क्रिस्टल जालीमा धातुको परमाणुहरू प्रतिनिधित्व गर्दछ, र छिटो चल्ने थोप्लाहरूले मुक्त इलेक्ट्रोनहरू प्रतिनिधित्व गर्दछ।

के यो छिटो देखिन्छ? त्यो किनभने इलेक्ट्रोनिक आन्दोलन साँच्चै छिटो छ! तर वास्तवमा, अनियमित गति, जुन यसको ठूलो अनुपातको लागि खाता हो, वर्तमानमा योगदान गर्दैन। जब अनियमित गति हटाइन्छ, बाँकी तलको ढिलो हेराइ जस्तै हुन्छ।

वास्तवमा, इलेक्ट्रोनहरूको दिशात्मक आन्दोलन थर्मल आन्दोलनको गति भन्दा धेरै ढिलो हुन्छ। इलेक्ट्रोनहरूको यो “पीसने” आन्दोलनलाई बहाव, वा “बहाव” भनिन्छ। कहिलेकाहीं, इलेक्ट्रोनहरू परमाणुहरूसँग टक्करको कारण विपरीत दिशामा दौडनेछन्। तर सामान्यतया, इलेक्ट्रोनहरू एक दिशामा सर्छन्।

यदि विद्युतीय क्षेत्रले दिशा परिवर्तन गर्छ भने, इलेक्ट्रोन बहावको दिशा पनि परिवर्तन हुनेछ।

तसर्थ, यस प्रकारको दिशात्मक आन्दोलनको अर्थ हो कि एक निश्चित समयमा प्रवाहमा भाग लिने सबै इलेक्ट्रोनहरूको गतिको योग शून्य होइन, तर सामान्यतया एक निश्चित दिशामा हुन्छ। यो दिशा कुनै पनि समयमा परिवर्तन गर्न सकिन्छ, र यो वैकल्पिक वर्तमान को मामला हो।

तसर्थ, वर्तमान विद्युतीय चार्जको “दिशात्मक आन्दोलन” होइन जति यो विद्युतीय चार्जको “सामूहिक आन्दोलन” हो।

कन्डक्टरमा वर्तमानको परिमाण वर्तमान तीव्रता द्वारा व्यक्त गरिएको छ। हालको तीव्रता एक इकाई समयमा कन्डक्टरको क्रस-सेक्शनबाट गुजरने बिजुलीको मात्राको रूपमा परिभाषित गरिएको छ, अर्थात्

हामीले केहि भौतिक मात्राहरू सिकेका छौं जसमा “तीव्रता” शब्द समावेश छ, जस्तै विद्युत क्षेत्र तीव्रता र चुम्बकीय इन्डक्शन तीव्रता। तिनीहरू सामान्यतया प्रति एकाइ समय, एकाइ क्षेत्र (वा एकाइ भोल्युम, एकाइ ठोस कोण) को विभाजन प्रतिनिधित्व गर्दछ। यद्यपि, वर्तमान तीव्रतामा “तीव्रता” शब्दले क्षेत्रको हालको विभाजनलाई प्रतिबिम्बित गर्दैन।

वास्तवमा, अर्को भौतिक मात्रा क्षेत्रको वर्तमान वितरणको लागि जिम्मेवार छ, जुन वर्तमान घनत्व हो।

विद्युतीय प्रवाहको सार विद्युतीय चार्जको दिशात्मक आन्दोलन हो, त्यहाँ वर्तमान तीव्रता र बहाव गति बीच एक निश्चित सम्बन्ध हुनुपर्छ!

यो सम्बन्ध प्राप्त गर्नको लागि, हामीले पहिले अवधारणा-वाहक एकाग्रतालाई स्पष्ट गर्नुपर्छ, त्यो हो, एकाइ भोल्युममा वाहकहरूको संख्या, जुन  द्वारा व्यक्त गरिएको छ।

यो मानिन्छ कि कन्डक्टर क्रस सेक्शन हो, वाहक एकाग्रता हो, बहाव वेग हो, र चार्ज गरिएको चार्ज हो।

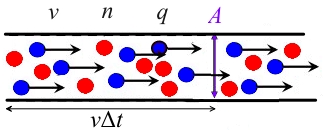
त्यसपछि सतहको बायाँ छेउमा रहेको कन्डक्टरमा चार्ज हुन्छ, र यी चार्जहरू निश्चित समयावधि भित्र सतहबाट पास हुन्छन्, त्यसैले

यो वर्तमान तीव्रता को एक माइक्रोस्कोपिक अभिव्यक्ति हो।

वर्तमान घनत्व भनेको करेन्टको क्षेत्रफलको विभाजन हो, त्यसैले वर्तमान घनत्वको परिमाण हो, तर यसलाई भेक्टरको रूपमा परिभाषित गरिएको छ, र दिशा भनेको सकारात्मक रूपमा चार्ज गरिएका वाहकहरूको बहाव वेग भेक्टरको दिशा हो, त्यसैले इलेक्ट्रोनहरूको बहाव धातु यस गतिबाट प्राप्त गर्न सकिन्छ, तलको उदाहरणको रूपमा।

तामाको तारलाई विचार गर्नुहोस्, मान्नुहोस् कि प्रत्येक तामाको परमाणुले वाहकको रूपमा इलेक्ट्रोनलाई योगदान गर्दछ। तामाको 1 मोल छ, यसको मात्रा छ, मोलर मास छ, घनत्व छ, त्यसपछि तामाको तारको वाहक एकाग्रता छ

Avogadro को स्थिर कहाँ छ। तामाको घनत्व पाइन्छ, र प्रतिस्थापन गरेर प्राप्त मान लगभग एकाइ/घन मिटर हो।

तामाको तारको त्रिज्या 0.8mm छ भनी मान्दै, वर्तमान प्रवाह 15A, = 1.6 C, र इलेक्ट्रोनहरूको बहाव वेग यस रूपमा गणना गरिन्छ।

यो देख्न सकिन्छ कि इलेक्ट्रोन को बहाव गति साँच्चै धेरै सानो छ।

सर्किटहरू अध्ययन गर्नेहरूका लागि, माथिको करेन्टको पूर्ण परिभाषा हो।

तर भौतिकशास्त्रमा, वर्तमानको माथिको परिभाषा वास्तवमा केवल एक संकीर्ण परिभाषा हो। अधिक सामान्य प्रवाहहरू कन्डक्टरहरूमा सीमित छैनन्, जबसम्म विद्युतीय चार्जहरूको चाल वर्तमान छ। उदाहरणका लागि, जब हाइड्रोजन एटमको इलेक्ट्रोनहरू न्यूक्लियसको वरिपरि घुम्छन्, यसको कक्षामा विद्युतीय प्रवाह बनाइन्छ।

मान्नुहोस् कि इलेक्ट्रोनिक चार्जको मात्रा हो र आन्दोलनको अवधि हो। त्यसपछि प्रत्येक पटक बितेको बेला, त्यहाँ लूपको कुनै पनि क्रस सेक्शनबाट यति ठूलो मात्रामा चार्ज हुन्छ, त्यसैले वर्तमान तीव्रता अवधि, फ्रिक्वेन्सी र कोणीय वेग बीचको सम्बन्धमा आधारित हुन्छ, र वर्तमानलाई पनि यस रूपमा व्यक्त गर्न सकिन्छ।

अर्को उदाहरणको लागि, चार्ज गरिएको मेटल डिस्क, यसको अक्षको वरिपरि घुम्ने, विभिन्न त्रिज्यासँग लूप करेन्टहरू पनि बनाउँछ।

यस प्रकारको प्रवाह सामान्य प्रवाहकीय प्रवाह होइन र जुल ताप उत्पन्न गर्न सक्दैन! वास्तविक सर्किट बनाउन सक्दैन।

अन्यथा, के तपाईले मलाई हाइड्रोजन एटमको इलेक्ट्रोनहरू द्वारा प्रति सेकेन्ड जूल तातो उत्पन्न गर्ने हिसाब दिनुहुनेछ?

वास्तवमा, वैक्यूममा वर्तमानले ओमको नियमलाई पूरा गर्दैन। किनभने, भ्याकुममा चार्ज गरिएका कणहरूको आन्दोलनबाट बनेको विद्युतीय प्रवाहको लागि, वाहकहरू धातुमा रहेको जालीजस्तै टक्कर हुँदैनन्, त्यसैले भ्याकुमको कुनै प्रतिरोध र कुनै चालकता हुँदैन।

बिजुली चार्जको आन्दोलनले बिजुली प्रवाह उत्पन्न गर्दछ, र बिजुली चार्जले नै विद्युतीय क्षेत्रलाई उत्तेजित गर्दछ। यो गलतफहमी पैदा गर्न सजिलो छ। त्यसकारण धेरै मानिसहरूले विद्युतीय प्रवाह बनाउने चार्ज गरिएका कणहरूको विद्युतीय क्षेत्र खुला हुनुपर्छ भन्ने सोच्छन्। तर वास्तवमा, सामान्य कन्डक्टरमा प्रवाहक प्रवाहको लागि, धेरै संख्यामा सकारात्मक चार्ज गरिएको धातु आयनहरू मिलेर बनेको पृष्ठभूमिमा क्यारियरहरू प्रवाह हुन्छन्, र कन्डक्टर आफैं तटस्थ हुन्छ!

हामी प्राय: यस प्रकारको विशेष प्रवाहलाई “समान प्रवाह” भन्छौं। यहाँ समतुल्य भनेको सामान्य प्रवाह प्रवाहको रूपमा समान आधारमा चुम्बकीय क्षेत्र उत्पन्न गर्दछ!

रिमाइन्डर: सर्किट विश्लेषणमा “समान सर्किट” संग यहाँ “समान वर्तमान” भ्रमित नगर्नुहोस्।

वास्तवमा, जब हामीले पहिलो पटक चुम्बकीय क्षेत्रको अध्ययन गर्यौं, बायोट-सफरको नियममा विद्युतीय प्रवाह सामान्यीकृत विद्युतीय प्रवाह थियो जसमा यो बराबर प्रवाह समावेश थियो। निस्सन्देह, म्याक्सवेलको समीकरणहरूमा प्रवाह प्रवाहले सामान्यीकृत प्रवाहलाई पनि जनाउँछ।

फोटोइलेक्ट्रिक प्रभावको अध्ययन गर्नेहरूलाई थाहा छ कि जब फोटोइलेक्ट्रोन क्याथोडबाट एनोडमा जान्छ, यदि हावाको प्रभावलाई बेवास्ता गरियो भने, यो प्रवाह भ्याकुममा विद्युतीय चार्जहरूको आन्दोलनको कारणले हुन्छ, र त्यहाँ कुनै प्रतिरोध हुँदैन, त्यसैले यो हुन्छ। ओमको नियम द्वारा प्रतिबन्धित छैन।

त्यसोभए, के यो भौतिक विज्ञानमा विद्युतीय प्रवाहको बारेमा मात्र कुरा हो?

होइन! त्यहाँ पनि दुई प्रकार छन्, अर्थात् चुम्बकीय वर्तमान र विस्थापन वर्तमान।

तिनीहरू पनि दुई बराबर धाराहरू हुन्, जसलाई नामले सुझाव दिन्छ, चुम्बकत्वको व्याख्या गर्न पनि प्रस्तुत गरिएको छ। अर्को शब्दमा भन्नुपर्दा, तिनीहरू अहिलेको “चार्ज आन्दोलन” को आधारभूत विशेषताबाट टाढिएका छन्!

त्यो अचम्मको छ! त्यहाँ कुनै विद्युतीय चार्ज आन्दोलन छैन, त्यसोभए यसलाई किन विद्युत प्रवाह भनिन्छ?

चिन्ता नगर्नुहोस्, र मेरो कुरा बिस्तारै सुन्नुहोस्।

पहिले चुम्बकीय प्रवाह हेरौं।

यो फेला पर्‍यो कि चुम्बकत्व बिजुलीको आन्दोलनको कारणले हुन्छ (अहिलेको लागि स्पिनको आन्तरिक गुणहरूद्वारा चुम्बकत्वको व्याख्यालाई विचार गर्दैन)। प्राकृतिक चुम्बकत्वको व्याख्या गर्न, फ्रान्सेली भौतिकशास्त्री एम्पेरेले “आणविक परिसंचरण” को परिकल्पना अगाडि राखे।

तलको चित्रमा देखाइए अनुसार, कुनै पनि परमाणु वा अणुलाई केन्द्रको वरिपरि घुम्ने बिजुली चार्ज भएको मान्न सकिन्छ, एउटा सानो लूप करेन्ट बनाउँछ, अर्थात् “आणविक परिसंचरण”।

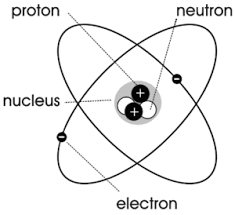
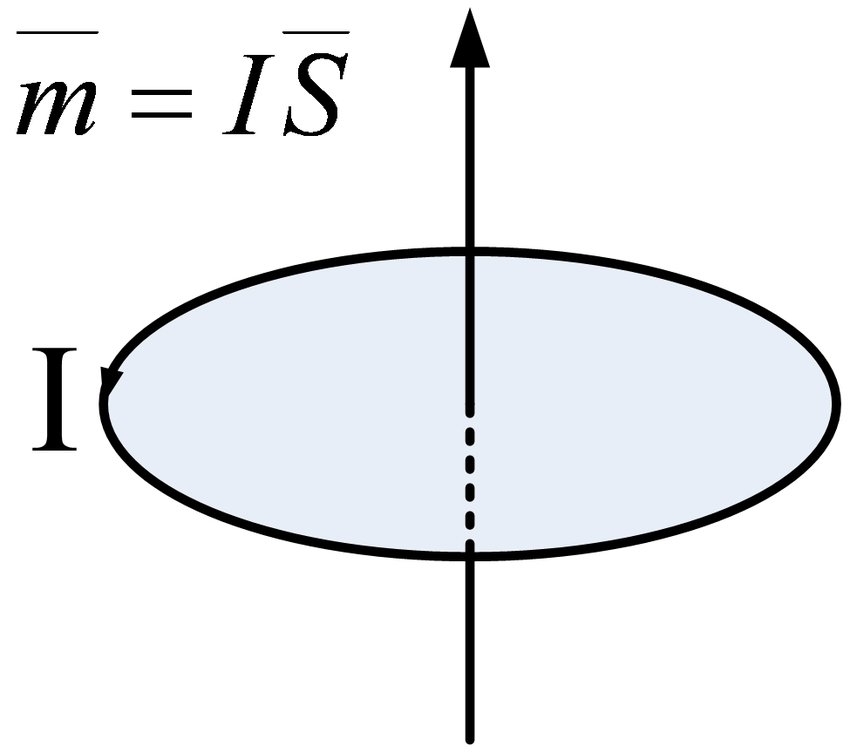
विद्युतीय प्रवाहले चुम्बकीय क्षेत्रलाई उत्तेजित गर्छ भन्ने नियम अनुसार, यो आणविक परिसंचरणले चुम्बकीय क्षण भनिने भौतिक मात्रा उत्पादन गर्नेछ। यसको आकार आणविक परिसंचरणले आणविक परिसंचरणको समतुल्य वर्तमानले गुणा गरेर घेरिएको क्षेत्र हो, र यसको दिशा परिसंचरणको दिशासँग दायाँ-हात सर्पिल सम्बन्धमा छ, अर्थात्।

जाहिर छ, चुम्बकीय क्षणको दिशा ठ्याक्कै परिसंचरण करन्टले बनेको चुम्बकीय क्षेत्रको दिशासँगै हुन्छ।

.

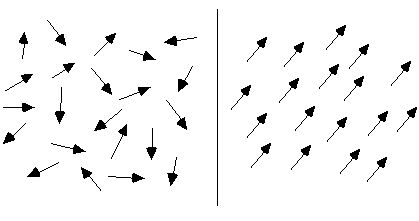
सामान्य परिस्थितिमा, पदार्थको आणविक परिसंचरणको व्यवस्था अस्तव्यस्त हुन्छ, त्यसैले पदार्थ चुम्बकीय हुँदैन, जस्तै तल चित्रको बायाँ तिर देखाइएको छ। बाह्य चुम्बकीय क्षेत्रको अधीनमा हुँदा, यी आणविक परिसंचरणहरू लगभग सफासँग व्यवस्थित हुनेछन्। तलको चित्रको दायाँ छेउमा देखाइएझैं, तिनीहरूका चुम्बकीय पलहरूलाई सम्भव भएसम्म एउटै दिशामा व्यवस्थित गरिन्छ, जसरी अनगिन्ती साना चुम्बकीय सुईहरू जम्मा भएर कुल चुम्बकीय क्षेत्र बनाउँछन्, र तिनीहरूबाट बनेको सम्पूर्ण सामग्री चुम्बकीय हुन्छ।

मानौं त्यहाँ एक बेलनाकार चुम्बक छ, भित्री आणविक परिसंचरणलाई राम्ररी व्यवस्थित गरिएको छ, र चुम्बक खण्डको छेउमा प्रत्येक आणविक परिसंचरणका खण्डहरू एक ठूलो परिसंचरण बनाउनको लागि एकसाथ जोडिएका छन्, तलको चित्रमा देखाइएको छ।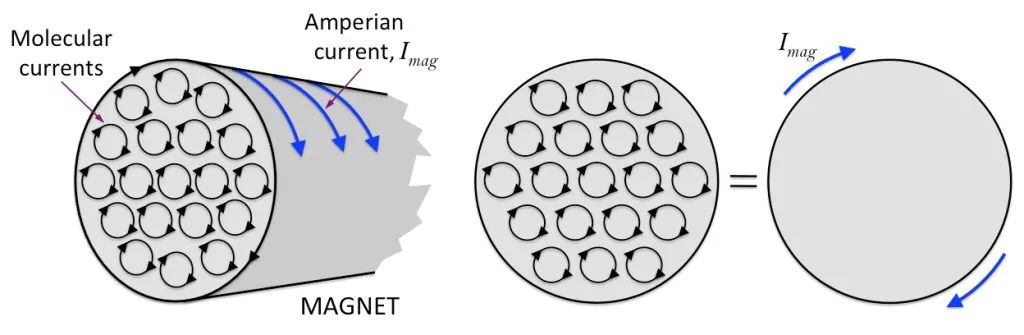

यसको आधारमा, हामी सोच्न सक्छौं कि बार चुम्बक एक ऊर्जावान सोलेनोइड जस्तै हो। अर्को शब्दमा भन्नुपर्दा, चुम्बकको सतहमा एउटा अदृश्य विद्युत् प्रवाह छ! यस प्रकारको वर्तमान जडान र प्रयोग गर्न सकिँदैन। यो चुम्बक को सतह मा सीमित छ। हामी यसलाई “बाइंडिंग करन्ट” वा “चुम्बकीय प्रवाह” भन्छौं।

तसर्थ, चुम्बकीय प्रवाह एक करेन्ट हो, किनकि यो वास्तविक विद्युतीय चार्जहरूको आन्दोलनबाट बनेको करेन्ट जस्तै हो, जसले चुम्बकीय क्षेत्रलाई समान रूपमा उत्पन्न गर्न सक्छ!

विस्थापन वर्तमानलाई फेरि हेरौं।

एम्पियरको लूप प्रमेय अनुसार, बन्द मार्गमा चुम्बकीय क्षेत्र बलको अभिन्न यो मार्गले घेरिएको कुनै पनि घुमाउरो सतहमा वर्तमान घनत्वको प्रवाह बराबर हुन्छ, अर्थात्, यो प्रमेयलाई गणितमा स्टोक्स प्रमेय भनिन्छ। यसले हामीलाई बताउँछ कि कुनै पनि बन्द मार्गमा भेक्टरको इन्टिग्रल यसको कर्लको प्रवाह (यहाँ) बन्द मार्गले बाँधिएको कुनै पनि सतहमा बराबर हुनुपर्छ।

यो एक गणितीय प्रमेय भएकोले, यो सधैं सही हुनुपर्छ, किनभने गणित एक तार्किक प्रणाली हो जो axioms मा आधारित छ।

त्यसैले, एम्पीयर लूप प्रमेय सधैं धारण गर्नुपर्छ!

यद्यपि, प्रतिभाशाली स्कटिश भौतिकशास्त्री म्याक्सवेलले पत्ता लगाए कि जब अस्थिर वर्तमान सर्किटको सामना गर्नुपर्‍यो, एम्पियर लूप प्रमेय विरोधाभासी थियो।

सामान्य अस्थिर वर्तमान क्यापेसिटर को चार्ज र डिस्चार्ज को समयमा हुन्छ। तलको चित्रमा देखाइए अनुसार, क्यापेसिटर चार्ज गर्ने छोटो अवधिमा एक अस्थिर वर्तमान छ।

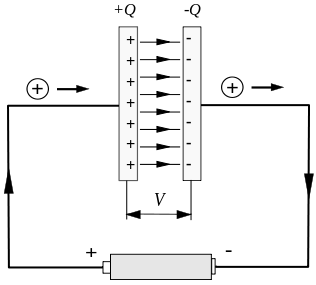
तर सर्किट क्यापेसिटर प्लेटहरू बीच विच्छेद गरिएको छ, जसले गम्भीर समस्या निम्त्याउँछ।

मानौं कि हामीले तारलाई बाइपास गर्ने बन्द मार्गलाई विचार गर्छौं, तलको चित्रमा देखाइए अनुसार, C द्वारा चिन्ह लगाइएको वृत्त, र त्यससँगको घुमाउरो सतहलाई सीमाना रूपमा चयन गर्न सकिन्छ। चित्रमा, C आफैं र क्यापेसिटर भरी घेरिएको गोलाकार विमान चयन गरिएको छ। बायाँ प्लेटको घुमाउरो सतह।

गोलाकार सतह अनुसार, यो देख्न सकिन्छ कि घुमाउरो सतह अनुसार, तर चुम्बकीय क्षेत्र बल को एक लुप अभिन्न को रूप मा, यसको मान निर्धारण गर्नुपर्छ!

कसरि गर्ने?

म्याक्सवेल विश्वास गर्छन् कि एम्पियरको लूप प्रमेय स्थापित हुनुपर्छ। अब जब त्यहाँ समस्या छ, यो हुनुपर्दछ किनभने वर्तमानको एक अंश हामीले पहिले पत्ता लगाएको छैन, तर यो अवस्थित छ!

त्यसोभए, वर्तमानको यो भाग कसरी पत्ता लगाउने?

समस्या प्लेटहरू बीचको भएकोले, प्लेटहरू बीचबाट सुरु गर्नुहोस्।

विश्लेषणको माध्यमबाट, म्याक्सवेलले चार्ज वा डिस्चार्जिङको ख्याल नगरी पत्ता लगाए, त्यहाँ क्यापेसिटर प्लेटहरू बीचको भौतिक मात्रा जहिले पनि वर्तमानको परिमाण र दिशासँग सिंक्रोनाइज हुन्छ। यो विद्युतीय विस्थापन भेक्टरको प्रवाहको समय व्युत्पन्न हो, अर्थात्, यसलाई विस्थापन वर्तमानको रूपमा परिभाषित गरिएको छ।

यदि यो भाग पहिले पत्ता नलागेको धाराको भाग हो भनेर मानिन्छ भने, पूर्ण प्रवाह अहिले हो। अर्थात्, प्लेटहरू बीचको सर्किट विच्छेदन भए तापनि, विद्युतीय विस्थापन प्रवाहको व्युत्पन्न र करेन्टको योगफल सँगै, समग्र रूपमा, सबै समयमा प्रवाहको निरन्तरता सुनिश्चित गर्नुहोस्।

अघिल्लो विरोधाभासमा फर्केर, हामी अब जान्दछौं कि, स्टोक्सको प्रमेयको आवश्यकता अनुसार, बन्द सतहको लागि वर्तमान घनत्वको प्रवाह गणना गर्दा, विस्थापन प्रवाहको घनत्वलाई पनि विचार गर्नुपर्छ, अर्थात्, पूर्ण एम्पियर लुप। प्रमेय यसैले, यो नयाँ वर्तमान घटक “खोज” गरेर, एम्पियर लूप प्रमेय को संकट हल भयो!

कारण यहाँ “परिचय” प्रयोग गरिएको छैन, तर यहाँ “खोज” प्रयोग गरिएको छ। के म जोड दिन चाहन्छु कि यस प्रकारको वर्तमान एक गणितीय क्षतिपूर्ति होइन, तर एक वास्तविक कुरा हो, तर यो पहिले पत्ता लागेको थिएन।

यो पहिलो स्थानमा किन अवस्थित छ? किनभने यसले विद्युतीय प्रवाहको रूपमा कार्य गर्दछ, प्रवाह प्रवाह जस्तै, यसले चुम्बकीय क्षेत्रलाई समान रूपमा उत्तेजित गर्दछ, बाहेक त्यहाँ विद्युतीय चार्जहरूको कुनै चाल छैन, कुनै तार आवश्यक पर्दैन, र कुनै जुल ताप उत्पन्न गर्न सकिँदैन, त्यसैले यसलाई बेवास्ता गरिएको छ!

तर यो वास्तवमा आफैंमा अवस्थित छ, केवल एक कम प्रोफाइल राख्नुहोस्, यो चुपचाप त्यहाँ चुम्बकीय क्षेत्र सबै समय रोमाञ्चक गरिएको छ!

अर्को शब्दमा, जब हामी चुम्बकीय क्षेत्र सामना गर्छौं, वर्तमान को मूल परिभाषा धेरै संकीर्ण छ। विद्युतीय प्रवाहको सार विद्युतीय चार्जको गति होइन, यो चुम्बकीय क्षेत्रलाई उत्तेजित गर्न सक्ने चीज हुनुपर्छ।

हाल सम्म, वर्तमान को धेरै रूपहरु पेश गरिएको छ। तिनीहरू सबै वस्तुगत रूपमा अवस्थित छन्, र तिनीहरूमा के समान छ कि सबै धाराहरूले चुम्बकीय क्षेत्रलाई समान रूपमा उत्तेजित गर्न सक्छन्।