什么是电流？ 首先回忆一下，我们学过的电流的定义是什么？

很简单，带电粒子在导体中的定向运动是电流。

只有当物质具有可以自由移动的带电粒子时，它才能传输电流，即导电。 这些参与传导的带电粒子称为载流子。 例如，对于金属，只有原子的外层电子可以作为载流子。

电流定义中的“定向运动”经常被误解。 很多人认为它是指有一定方向的运动，当然不是！ 交流电路中电子的运动方向不会改变吗？

其实，定向运动是相对于“随机运动”而言的！

由于电子是微观粒子，它们必须一直处于热运动中。 热运动是一种随机运动，如下图所示。

这个动作其实非常快。 例如，在室温下的金属中，电子热运动的速度在每秒数百公里的数量级！

如果仔细观察这个随机运动，你会发现每个粒子的运动方向在任何时刻都是随机的。 如果将这些粒子的速度矢量相加，结果几乎为零。

现在给导体加上电场，电子在随机运动的基础上叠加定向运动。 假设电场向左移动一段时间，电子的运动如下所示。 红球代表晶格上的金属原子，快速移动的点代表自由电子。

它看起来很快吗？ 那是因为电子运动真的很快！ 但实际上，占其中很大比例的随机运动对电流没有贡献。 当随机运动消除后，剩下的就像下面的慢看一样。

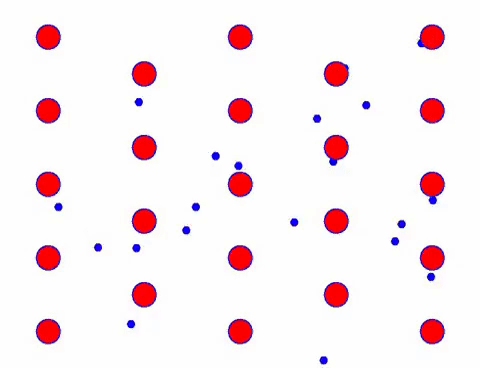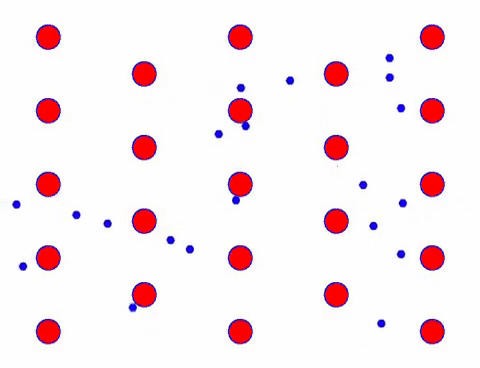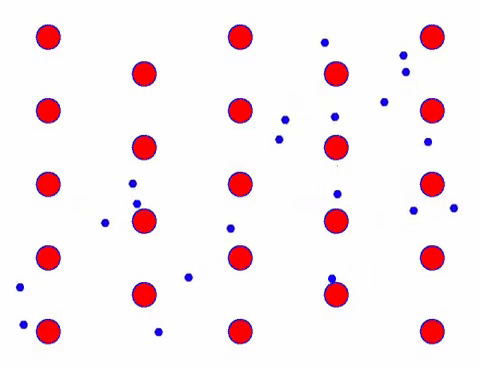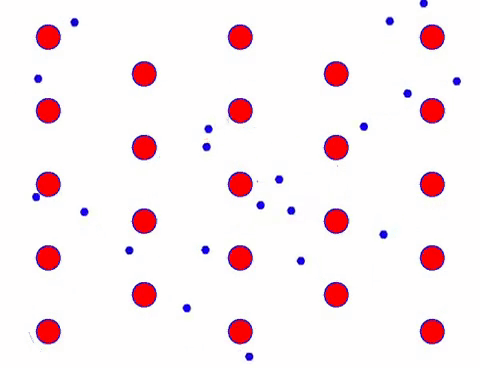
Indeed, the directional movement of electrons is much slower than the speed of thermal movement. This “grinding” movement of electrons is called drift, or “drift”. Sometimes, electrons will run in the opposite direction because of collisions with atoms. But in general, electrons move in one direction.

如果电场改变方向，电子漂移的方向也会改变。

因此，这种定向运动意味着在某一时刻参与传导的所有电子的速度之和不为零，而一般是在某一方向。 这个方向可以随时改变，交流就是这种情况。

因此，电流与其说是电荷的“定向运动”，不如说是电荷的“集体运动”。

导体中电流的大小用电流强度表示。 电流强度定义为单位时间内通过导体横截面的电量，即

我们已经学习了一些包含“强度”一词的物理量，例如电场强度和磁感应强度。 它们一般代表单位时间、单位面积（或单位体积、单位立体角）的比重。 但是，当前强度中的“强度”一词并不反映该区域的当前分配。

事实上，还有另一个物理量负责电流向面积的分布，这就是电流密度。

既然电流的本质是电荷的定向运动，那么电流强度和漂移速度肯定有一定的关系！

为了得到这个关系，首先要明确一个概念——载流子浓度，即单位体积内载流子的数量，用表示。

假设导体截面为，载流子浓度为，漂移速度为，带电电荷为。

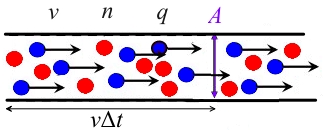
那么表面左侧导体中的电荷为，这些电荷会在一定时间内通过表面，所以

这是电流强度的微观表达。

电流密度是电流对面积的分配，所以电流密度的大小为金属可以从这个速度获得，如下面的例子。

考虑一根铜线，假设每个铜原子贡献一个电子作为载流子。 有1mol铜，它的体积是，摩尔质量是，密度是，那么铜线的载流子浓度是

阿伏伽德罗常数在哪里。 求出铜的密度，代入得到的数值约为单位/立方米。

假设铜线半径为0.8mm，流过的电流为15A，=1.6C，计算电子漂移速度为

可以看出，电子的漂移速度确实很小。

对于学习电路的人来说，以上就是电流的完整定义。

但在物理学中，上述电流的定义实际上只是一个狭义的定义。 更一般的电流不限于导体，只要电荷的运动是电流。 例如，当氢原子的电子围绕原子核运动时，在其轨道上形成电流。

假设电荷量为 ，运动周期为 。 那么每次经过时，都会有如此大量的电荷通过环路的任何截面，因此电流强度是基于周期、频率和角速度之间的关系，电流也可以表示为

再比如，一个带电的金属圆盘，围绕其轴旋转，也会形成不同半径的回路电流。

这种电流不是正常的传导电流，不会产生焦耳热！ 不能形成真正的电路。

不然你给我算一下，氢原子的电子每秒产生多少焦耳热？

事实上，真空中的电流并不满足欧姆定律。 因为，对于带电粒子在真空中运动形成的电流，载流子不会像金属中的晶格那样发生碰撞，所以真空没有电阻，也没有电导。

电荷的运动产生电流，电荷本身激发电场。 这很容易引起误解。 因此，许多人认为形成电流的带电粒子的电场必须暴露。 但实际上，对于一般导体中的传导电流，载流子是在由大量带正电的金属离子组成的背景上流动的，而导体本身是中性的！

我们常称这种特殊电流为“等效电流”。 这里的等效是指它产生的磁场与普通传导电流相同！

提醒：不要将这里的“等效电流”与电路分析中的“等效电路”混淆

事实上，当我们第一次研究磁场时，比奥-萨法尔定律中的电流就是包含这个等效电流的广义电流。 当然，麦克斯韦方程组中的传导电流也指广义电流。

研究过光电效应的人都知道，当光电子从阴极漂移到阳极时，如果忽略空气的影响，这个电流是由电荷在真空中的运动引起的，没有阻力，所以不受欧姆定律限制。

那么，这是物理学中唯一关于电流的东西吗？

不！ 也有励磁电流和位移电流两种。

它们也是两个等效的电流，顾名思义，它们也是用来解释磁性的。 也就是说，他们已经脱离了当前“冲锋运动”的基本特征！

太棒了！ 没有电荷运动，为什么可以称为电流呢？

别着急，听我慢慢说。

我们先来看看磁化电流。

发现磁性是由电的运动引起的（暂不考虑用自旋的内在特性来解释磁性）。 为了解释自然磁性，法国物理学家安培提出“分子循环”假说。

如下图所示，任何一个原子或分子都可以看作是有一个电荷围绕中心旋转，形成一个微小的回路电流，即“分子循环”。

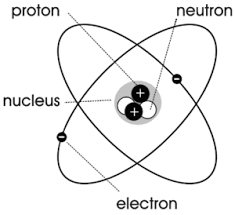
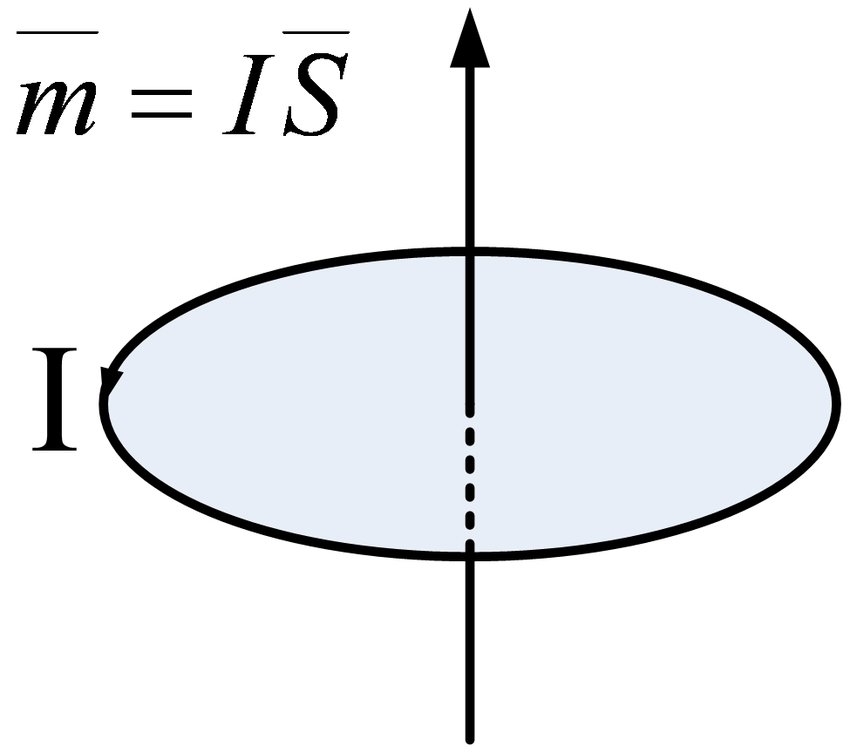
根据电流激发磁场的定律，这种分子循环会产生一个物理量，称为磁矩。 其大小为分子环流所围成的面积乘以分子环流的当量流，其方向与环流方向呈右手螺旋关系，即

显然，磁矩的方向正好沿着环流形成的磁场方向

.

一般情况下，物质分子循环的排列是混乱的，所以该物质是没有磁性的，如下图左侧所示。 当受到外磁场作用时，这些分子循环会近似整齐排列。 如下图右侧所示，它们的磁矩尽可能地排列在一个方向，就像无数个小磁针聚集在一起形成一个总磁场，由它们组成的整个材料都具有磁性。

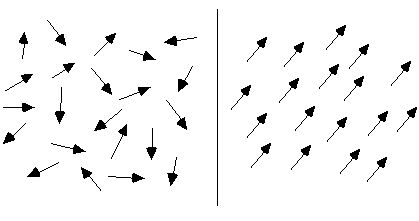
假设有一个圆柱状的磁铁，内部分子循环排列整齐，磁铁段边缘的每个分子循环段连接在一起，形成一个大循环，如下图所示。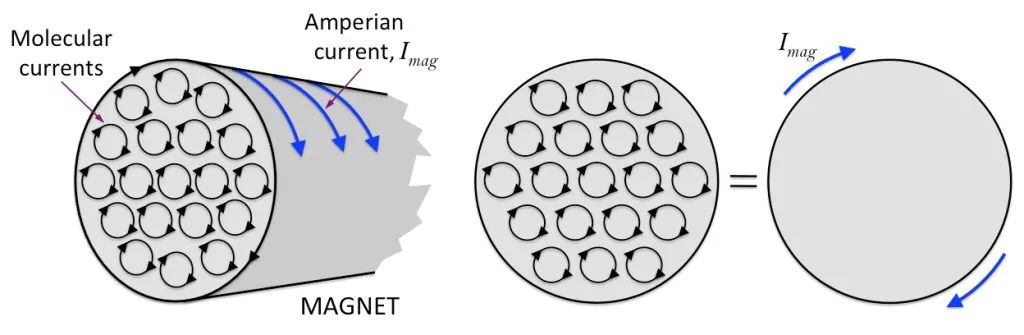

基于此，我们可以认为条形磁铁就像一个通电的螺线管。 也就是说，有一股无形的电流纠缠在磁铁的表面！ 这种电流不能接通使用。 它被限制在磁铁的表面。 我们称其为“结合电流”或“磁化电流”。

所以磁化电流是电流，因为它和真实电荷运动形成的电流一样，可以等效地产生磁场！

我们再来看看位移电流。

根据安培环路定理，闭合路径上磁场强度的积分等于以该路径为界的任意曲面上的电流密度通量，即该定理在数学上称为斯托克斯定理。 它告诉我们，向量沿任何闭合路径的积分必须等于其卷曲（此处）到以闭合路径为界的任何表面的通量。

既然是数学定理，就一定是正确的，因为数学是建立在公理基础上的逻辑系统。

因此，安培环定理必须始终成立！

然而，天才的苏格兰物理学家麦克斯韦发现，当面对不稳定的电流电路时，安培环定理是矛盾的。

典型的不稳定电流发生在电容器的充电和放电过程中。 如下图所示，电容器在短时间充电过程中存在不稳定的电流。

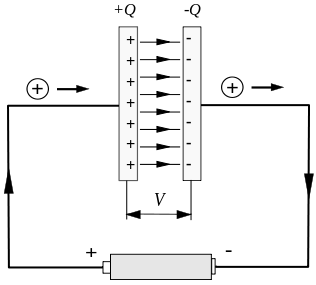
但电路在电容器极板之间断开，这将导致严重的问题。

假设我们考虑一条绕过导线的闭合路径，如下图所示，用C标记的圆，以它为边界的曲面可以任意选择。 在图中，选择了由 C 本身包围并穿过电容器的圆形平面。 左板的曲面。

根据圆曲面可以看出，根据曲面，但是作为磁场强度的环积分，应该确定它的值！

怎么做？

麦克斯韦认为安培环定理必须成立。 现在出现问题，一定是因为电流的一部分之前我们没有发现，但它确实存在！

那么，如何找出这部分电流呢？

由于问题出在板之间，因此从板之间开始。

通过分析，麦克斯韦发现，无论充电还是放电，电容器极板之间始终存在一个与电流大小和方向同步的物理量。 它是电位移矢量的通量的时间导数，即定义为位移电流。

如果认为这部分是之前未被发现的电流部分，那么完整的电流就是现在。 也就是说，虽然极板之间的电路是断开的，但是电位移通量的导数和电流之和，作为一个整体，始终保证了电流的连续性。

回到前面的矛盾，我们现在知道，根据斯托克斯定理的要求，在计算闭合曲面的电流密度通量时，还应考虑位移电流的密度，即完整的安培回路因此定理是，通过“发现”这个新的电流分量，安培环定理的危机就解决了！

之所以这里不用“介绍”，而是用“发现”。 我要强调的是，这种电流不是数学补偿，而是真实存在的，只是以前没有发现过。

为什么它首先存在？ 因为它充当电流，就像传导电流一样，它等效地激发了磁场，只是没有电荷的运动，不需要电线，也不会产生焦耳热，所以一直被忽略！

但它其实是自己存在的，只是低调一点，它一直在默默地激发着那里的磁场！

换句话说，当我们面对磁场时，电流的原始定义太狭窄了。 电流的本质不是电荷的运动，它应该是能激发磁场的东西。

到目前为止，已经介绍了几种形式的电流。 它们都是客观存在的，它们的共同点是所有的电流都能同等地激发磁场。