विद्युत धारा क्या है? पहले याद कीजिए कि हमने धारा की परिभाषा क्या सीखी है?

काफी सरलता से, एक चालक में आवेशित कणों की दिशात्मक गति एक विद्युत धारा होती है।

Only when a substance has charged particles that can move freely, it can transmit electric current—that is, conduct electricity. These charged particles that participate in conduction are called carriers. For metals, for example, only the outer electrons of atoms can act as carriers.

The “directional movement” in the definition of electric current is often misunderstood. Many people think it refers to movement with a certain direction, of course not! Doesn’t the direction of movement of the electrons in the AC circuit change?

वास्तव में, ओरिएंटियरिंग “यादृच्छिक आंदोलन” के सापेक्ष है!

चूंकि इलेक्ट्रॉन सूक्ष्म कण होते हैं, इसलिए उन्हें हर समय तापीय गति में रहना चाहिए। ऊष्मीय गति एक यादृच्छिक गति है, जैसा कि नीचे दिए गए चित्र में दिखाया गया है।

यह आंदोलन वास्तव में बहुत तेज है। उदाहरण के लिए, कमरे के तापमान पर धातुओं में, इलेक्ट्रॉनिक थर्मल गति की गति सैकड़ों किलोमीटर प्रति सेकंड के क्रम पर होती है!

If you look closely at this random movement, you will find that the direction of movement of each particle is random at any moment. If you add up the velocity vectors of these particles, the result is almost zero.

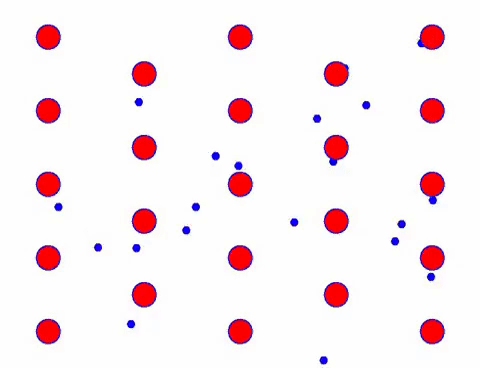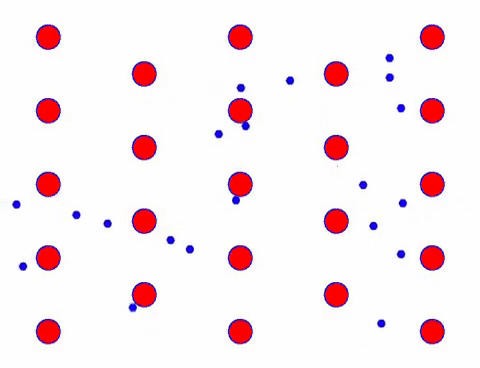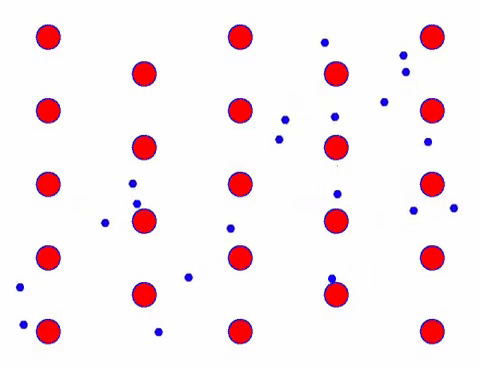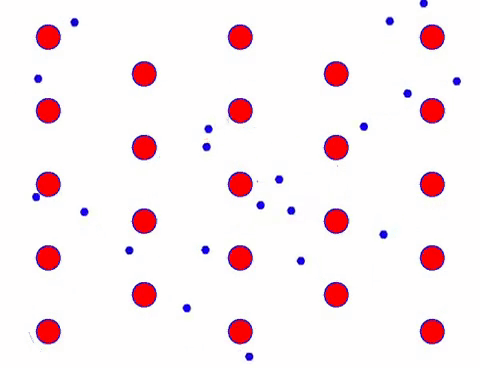
अब कंडक्टर में एक विद्युत क्षेत्र जोड़ें, और इलेक्ट्रॉन यादृच्छिक गति के आधार पर एक दिशात्मक गति को आरोपित करता है। यह मानते हुए कि विद्युत क्षेत्र एक निश्चित अवधि के लिए बाईं ओर है, इलेक्ट्रॉनों की गति निम्न की तरह दिखती है। लाल गेंदें क्रिस्टल जाली पर धातु के परमाणुओं का प्रतिनिधित्व करती हैं, और तेजी से चलने वाले बिंदु मुक्त इलेक्ट्रॉनों का प्रतिनिधित्व करते हैं।

क्या यह तेज़ दिखता है? ऐसा इसलिए है क्योंकि इलेक्ट्रॉनिक आंदोलन वास्तव में तेज़ है! लेकिन वास्तव में, यादृच्छिक गति, जो इसके एक बड़े हिस्से के लिए जिम्मेदार है, वर्तमान में योगदान नहीं करती है। जब यादृच्छिक गति समाप्त हो जाती है, तो बाकी नीचे की धीमी गति की तरह ही होती है।

Indeed, the directional movement of electrons is much slower than the speed of thermal movement. This “grinding” movement of electrons is called drift, or “drift”. Sometimes, electrons will run in the opposite direction because of collisions with atoms. But in general, electrons move in one direction.

If the electric field changes direction, the direction of electron drift will also change.

इसलिए, इस प्रकार की दिशात्मक गति का अर्थ है कि एक निश्चित समय पर चालन में भाग लेने वाले सभी इलेक्ट्रॉनों की गति का योग शून्य नहीं होता है, बल्कि आमतौर पर एक निश्चित दिशा में होता है। इस दिशा को किसी भी समय बदला जा सकता है, और यह प्रत्यावर्ती धारा का मामला है।

इसलिए, विद्युत आवेश की “दिशात्मक गति” उतनी नहीं है जितनी कि विद्युत आवेश की “सामूहिक गति” है।

चालक में धारा का परिमाण धारा की तीव्रता द्वारा व्यक्त किया जाता है। वर्तमान तीव्रता को एक इकाई समय में कंडक्टर के क्रॉस-सेक्शन से गुजरने वाली बिजली की मात्रा के रूप में परिभाषित किया जाता है, अर्थात्

We have learned some physical quantities that contain the word “intensity”, such as electric field intensity and magnetic induction intensity. They generally represent the apportionment per unit time, unit area (or unit volume, unit solid angle). However, the word “intensity” in the current intensity does not reflect the current apportionment of the area.

वास्तव में, एक अन्य भौतिक मात्रा क्षेत्र के लिए वर्तमान के वितरण के लिए जिम्मेदार है, जो वर्तमान घनत्व है।

चूंकि विद्युत प्रवाह का सार विद्युत आवेश की दिशात्मक गति है, इसलिए वर्तमान तीव्रता और बहाव गति के बीच एक निश्चित संबंध होना चाहिए!

In order to obtain this relationship, we must first clarify a concept-carrier concentration, that is, the number of carriers in a unit volume, which is expressed by .

It is assumed that the conductor cross section is, the carrier concentration is, the drift velocity is, and the charged charge is.

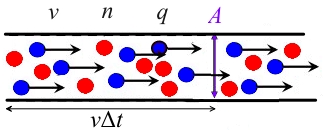
तब सतह के बाईं ओर कंडक्टर में चार्ज होता है, और ये चार्ज एक निश्चित अवधि के भीतर सतह से होकर गुजरेंगे, इसलिए

यह वर्तमान तीव्रता की सूक्ष्म अभिव्यक्ति है।

वर्तमान घनत्व क्षेत्र के लिए वर्तमान का विभाजन है, इसलिए वर्तमान घनत्व का परिमाण है, लेकिन इसे एक वेक्टर के रूप में परिभाषित किया गया है, और दिशा सकारात्मक चार्ज वाहक के बहाव वेग वेक्टर की दिशा है, इसलिए इलेक्ट्रॉनों का बहाव इस गति से धातु प्राप्त की जा सकती है, उदाहरण के लिए नीचे।

एक तांबे के तार पर विचार करें, यह मानते हुए कि प्रत्येक तांबे का परमाणु एक वाहक के रूप में एक इलेक्ट्रॉन का योगदान देता है। तांबे का 1 मोल है, इसका आयतन है, दाढ़ द्रव्यमान है, घनत्व है, तो तांबे के तार की वाहक सांद्रता है

अवोगाद्रो नियतांक कहाँ है। तांबे का घनत्व पाया जाता है, और प्रतिस्थापन से प्राप्त मान लगभग इकाई/घन मीटर होता है।

यह मानते हुए कि तांबे के तार की त्रिज्या 0.8 मिमी है, वर्तमान प्रवाह 15 ए, = 1.6 सी है, और इलेक्ट्रॉनों के बहाव वेग की गणना की जाती है

It can be seen that the drift speed of electrons is indeed very small.

सर्किट का अध्ययन करने वालों के लिए, उपरोक्त वर्तमान की पूरी परिभाषा है।

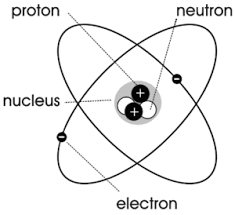
लेकिन भौतिकी में, वर्तमान की उपरोक्त परिभाषा वास्तव में केवल एक संकीर्ण परिभाषा है। अधिक सामान्य धाराएँ कंडक्टरों तक सीमित नहीं हैं, जब तक कि विद्युत आवेशों की गति चालू रहती है। उदाहरण के लिए, जब हाइड्रोजन परमाणु के इलेक्ट्रॉन नाभिक के चारों ओर घूमते हैं, तो उसकी कक्षा में एक विद्युत धारा बनती है।

Suppose the amount of electronic charge is and the period of movement is. Then every time that elapses, there is such a large amount of charge passing through any cross section of the loop, so the current intensity is based on the relationship between period, frequency and angular velocity, and the current can also be expressed as

For another example, a charged metal disk, rotating around its axis, also forms loop currents with different radii.

इस प्रकार की धारा सामान्य चालन धारा नहीं है और जूल ऊष्मा उत्पन्न नहीं कर सकती है! वास्तविक परिपथ नहीं बना सकते।

अन्यथा, क्या आप मुझे इस बात की गणना देंगे कि हाइड्रोजन परमाणु के इलेक्ट्रॉनों द्वारा प्रति सेकंड कितनी जूल ऊष्मा उत्पन्न होती है?

वास्तव में, निर्वात में धारा ओम के नियम को संतुष्ट नहीं करती है। क्योंकि, निर्वात में आवेशित कणों की गति से बनने वाले विद्युत प्रवाह के लिए, वाहक धातु में जाली के समान नहीं टकराते हैं, इसलिए निर्वात का कोई प्रतिरोध और कोई चालकता नहीं है।

The movement of electric charges generates electric current, and the electric charge itself excites the electric field. This is easy to cause a misunderstanding. Many people therefore think that the electric field of the charged particles that form the electric current must be exposed. But in fact, for the conduction current in a general conductor, carriers flow on a background composed of a large number of positively charged metal ions, and the conductor itself is neutral!

हम अक्सर इस प्रकार की विशेष धारा को “समतुल्य धारा” कहते हैं। यहाँ समतुल्य का अर्थ है कि यह एक सामान्य चालन धारा के समान चुंबकीय क्षेत्र उत्पन्न करता है!

Reminder: Do not confuse the “equivalent current” here with the “equivalent circuit” in circuit analysis

In fact, when we first studied the magnetic field, the electric current in Biot-Saffar’s law was the generalized electric current that contained this equivalent current. Of course, the conduction current in Maxwell’s equations also refers to the generalized current.

जिन लोगों ने फोटोइलेक्ट्रिक प्रभाव का अध्ययन किया है, वे जानते हैं कि जब फोटोइलेक्ट्रॉन कैथोड से एनोड में चला जाता है, अगर हवा के प्रभाव को नजरअंदाज कर दिया जाता है, तो यह करंट निर्वात में विद्युत आवेशों की गति के कारण होता है, और कोई प्रतिरोध नहीं होता है, इसलिए यह ओम के नियम द्वारा प्रतिबंधित नहीं है।

तो, क्या भौतिकी में विद्युत प्रवाह के बारे में यही एकमात्र चीज है?

नहीं! दो प्रकार के होते हैं, अर्थात् चुंबकीय धारा और विस्थापन धारा।

They are also two equivalent currents, which, as the name suggests, are also introduced to explain magnetism. In other words, they have broken away from the basic characteristic of the current “charge movement”!

वह आश्चर्यजनक है! कोई विद्युत आवेश गति नहीं है, तो इसे विद्युत प्रवाह क्यों कहा जा सकता है?

चिंता मत करो, और धीरे से मेरी बात सुनो।

आइए पहले मैग्नेटाइजिंग करंट को देखें।

यह पाया गया कि चुंबकत्व बिजली की गति के कारण होता है (फिलहाल स्पिन के आंतरिक गुणों द्वारा चुंबकत्व की व्याख्या पर विचार नहीं किया जाता है)। प्राकृतिक चुंबकत्व की व्याख्या करने के लिए, फ्रांसीसी भौतिक विज्ञानी एम्पीयर ने “आणविक परिसंचरण” की परिकल्पना को सामने रखा।

As shown in the figure below, any atom or molecule can be regarded as having an electric charge rotating around the center, forming a tiny loop current, that is, “molecular circulation”.

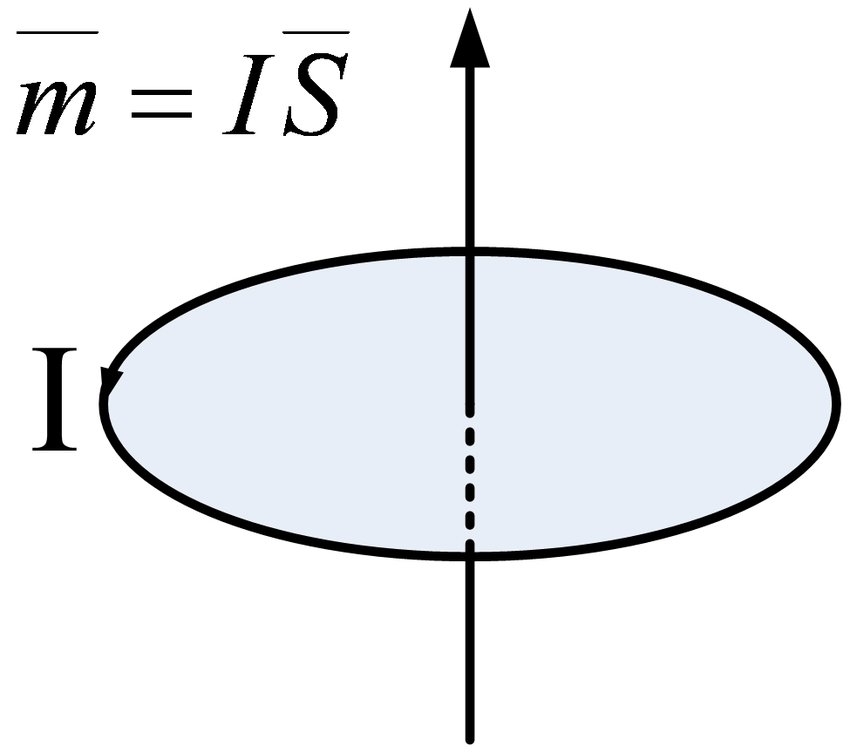
कानून के अनुसार कि विद्युत प्रवाह चुंबकीय क्षेत्र को उत्तेजित करता है, यह आणविक परिसंचरण एक भौतिक मात्रा उत्पन्न करेगा जिसे चुंबकीय क्षण कहा जाता है। इसका आकार आण्विक परिसंचरण के बराबर वर्तमान से गुणा आणविक परिसंचरण से घिरा क्षेत्र है, और इसकी दिशा परिसंचरण की दिशा के साथ दाएं हाथ के सर्पिल संबंध में है, अर्थात्

जाहिर है, चुंबकीय क्षण की दिशा परिसंचारी धारा द्वारा गठित चुंबकीय क्षेत्र की दिशा के साथ होती है

.

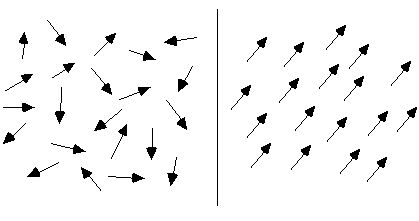
Under normal circumstances, the arrangement of the molecular circulation of a substance is chaotic, so the substance is not magnetic, as shown on the left side of the figure below. When subjected to an external magnetic field, these molecular circulations will be approximately neatly arranged. As shown on the right side of the figure below, their magnetic moments are arranged in one direction as much as possible, just like countless small magnetic needles gathered together to form a total magnetic field, and the whole material composed of them becomes magnetic.

मान लीजिए कि एक बेलनाकार चुंबक है, आंतरिक आणविक परिसंचरण बड़े करीने से व्यवस्थित है, और चुंबक खंड के किनारे पर प्रत्येक आणविक परिसंचरण के खंड एक बड़े परिसंचरण को बनाने के लिए एक साथ जुड़े हुए हैं, जैसा कि नीचे दिए गए चित्र में दिखाया गया है।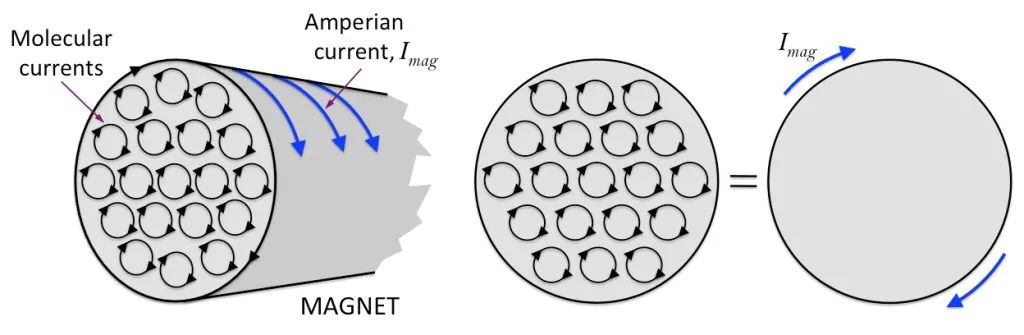

Based on this, we can think that a bar magnet is like an energized solenoid. In other words, there is an invisible current entangled on the surface of the magnet! This kind of current cannot be connected and used. It is confined to the surface of the magnet. We call it “binding current” or “magnetizing current”.

Therefore, the magnetizing current is a current, because it is the same as the current formed by the movement of real electric charges, which can equivalently generate a magnetic field!

Let’s look at the displacement current again.

एम्पीयर के लूप प्रमेय के अनुसार, बंद पथ पर चुंबकीय क्षेत्र की ताकत का अभिन्न अंग इस पथ से घिरे किसी भी घुमावदार सतह पर वर्तमान घनत्व के प्रवाह के बराबर है, अर्थात इस प्रमेय को गणित में स्टोक्स प्रमेय कहा जाता है। यह हमें बताता है कि किसी भी बंद पथ के साथ एक वेक्टर का अभिन्न अंग बंद पथ से घिरे किसी भी सतह पर उसके कर्ल (यहां) के प्रवाह के बराबर होना चाहिए।

चूंकि यह एक गणितीय प्रमेय है, यह हमेशा सही होना चाहिए, क्योंकि गणित स्वयंसिद्धों पर आधारित एक तार्किक प्रणाली है।

Therefore, the Ampere Loop Theorem must always hold!

हालांकि, प्रतिभाशाली स्कॉटिश भौतिक विज्ञानी मैक्सवेल ने पाया कि जब एक अस्थिर वर्तमान सर्किट का सामना करना पड़ा, तो एम्पीयर लूप प्रमेय विरोधाभासी था।

संधारित्र की चार्जिंग और डिस्चार्जिंग के दौरान विशिष्ट अस्थिर धारा होती है। जैसा कि नीचे दिए गए चित्र में दिखाया गया है, संधारित्र चार्जिंग की छोटी अवधि के दौरान एक अस्थिर धारा होती है।

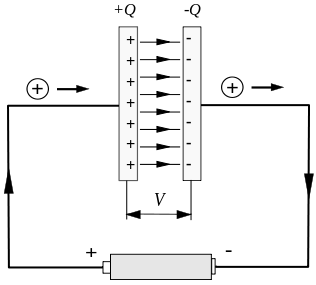
But the circuit is disconnected between the capacitor plates, which will cause a serious problem.

Suppose we consider a closed path that bypasses the wire, as shown in the figure below, the circle marked by C, and the curved surface with it as the boundary can be arbitrarily selected. In the figure, the circular plane enclosed by C itself and across the capacitor are selected. The curved surface of the left plate.

गोलाकार सतह के अनुसार, यह देखा जा सकता है कि घुमावदार सतह के अनुसार, लेकिन चुंबकीय क्षेत्र की ताकत के एक लूप अभिन्न के रूप में, इसका मूल्य निर्धारित किया जाना चाहिए!

कैसे करें?

Maxwell believes that the Ampere’s loop theorem must be established. Now that there is a problem, it must be because a part of the current has not been discovered by us before, but it does exist!

तो, करंट के इस हिस्से का पता कैसे लगाएं?

चूंकि समस्या प्लेटों के बीच है, इसलिए प्लेटों के बीच से शुरू करें।

विश्लेषण के माध्यम से, मैक्सवेल ने पाया कि चार्जिंग या डिस्चार्जिंग की परवाह किए बिना, कैपेसिटर प्लेटों के बीच हर समय एक भौतिक मात्रा होती है जो वर्तमान की परिमाण और दिशा के साथ सिंक्रनाइज़ होती है। यह विद्युत विस्थापन वेक्टर के प्रवाह का समय व्युत्पन्न है, अर्थात इसे विस्थापन धारा के रूप में परिभाषित किया गया है।

If it is considered that this part is the part of the current that has not been discovered before, then the complete current is now. That is to say, although the circuit between the plates is disconnected, the derivative of the electric displacement flux and the sum of the current together, as a whole , Ensure the continuity of the current at all times.

पिछले विरोधाभास पर वापस जाने पर, अब हम जानते हैं कि, स्टोक्स के प्रमेय की आवश्यकताओं के अनुसार, एक बंद सतह के लिए वर्तमान घनत्व के प्रवाह की गणना करते समय, विस्थापन धारा के घनत्व पर भी विचार किया जाना चाहिए, अर्थात पूर्ण एम्पीयर लूप प्रमेय इसलिए है, इस नए वर्तमान घटक की “खोज” करके, एम्पीयर लूप प्रमेय का संकट हल हो गया है!

कारण यहाँ “परिचय” का उपयोग नहीं किया गया है, लेकिन यहाँ “खोज” का उपयोग किया गया है। मैं जिस बात पर जोर देना चाहता हूं वह यह है कि इस तरह का करंट गणितीय मुआवजा नहीं है, बल्कि एक वास्तविक चीज है, लेकिन इसकी खोज पहले नहीं की गई है।

यह पहले स्थान पर क्यों मौजूद है? चूँकि यह विद्युत धारा के रूप में कार्य करता है, चालन धारा की तरह, यह एक चुंबकीय क्षेत्र को समान रूप से उत्तेजित करता है, सिवाय इसके कि विद्युत आवेशों की कोई गति नहीं होती है, किसी तार की आवश्यकता नहीं होती है, और कोई जूल ऊष्मा उत्पन्न नहीं की जा सकती है, इसलिए इसे अनदेखा कर दिया गया है!

But it actually exists by itself, just keep a low profile, it has been silently exciting the magnetic field there all the time!

दूसरे शब्दों में, जब हम एक चुंबकीय क्षेत्र का सामना करते हैं, तो धारा की मूल परिभाषा बहुत संकीर्ण होती है। विद्युत प्रवाह का सार विद्युत आवेश की गति नहीं है, यह कुछ ऐसा होना चाहिए जो चुंबकीय क्षेत्र को उत्तेजित कर सके।

अब तक, वर्तमान के कई रूपों को पेश किया गया है। वे सभी वस्तुनिष्ठ रूप से मौजूद हैं, और उनमें जो समानता है वह यह है कि सभी धाराएं चुंबकीय क्षेत्र को समान रूप से उत्तेजित कर सकती हैं।