- 09
- Dec
ධාරාව යනු කුමක්ද?
විදුලි ධාරාව යනු කුමක්ද? මුලින්ම මතක තබා ගන්න, අපි ඉගෙන ගත් ධාරාවේ නිර්වචනය කුමක්ද?

ඉතා සරලව, සන්නායකයක ආරෝපිත අංශුවල දිශානුගත චලනය විද්යුත් ධාරාවකි.
යම් ද්රව්යයකට නිදහසේ චලනය විය හැකි අංශු ආරෝපිත වූ විට පමණක් එයට විද්යුත් ධාරාව සම්ප්රේෂණය කළ හැකිය – එනම් විදුලිය සන්නයනය කළ හැකිය. සන්නායකතාවයට සහභාගී වන මෙම ආරෝපිත අංශු වාහකයන් ලෙස හැඳින්වේ. උදාහරණයක් ලෙස ලෝහ සඳහා වාහකයන් ලෙස ක්රියා කළ හැක්කේ පරමාණුවල බාහිර ඉලෙක්ට්රෝන පමණි.
විද්යුත් ධාරාවෙහි නිර්වචනයේ “දිශානුගත චලනය” බොහෝ විට වරදවා වටහාගෙන ඇත. බොහෝ අය සිතන්නේ එය නිශ්චිත දිශාවකින් චලනය වන බවයි, ඇත්ත වශයෙන්ම නොවේ! AC පරිපථයේ ඉලෙක්ට්රෝන චලනය වන දිශාව වෙනස් නොවේද?
ඇත්ත වශයෙන්ම, දිශානතිය “අහඹු චලනය” ට සාපේක්ෂයි!
ඉලෙක්ට්රෝන යනු අන්වීක්ෂීය අංශු බැවින් ඒවා සෑම විටම තාප චලිතයේ තිබිය යුතුය. පහත රූපයේ දැක්වෙන පරිදි තාප චලිතය අහඹු චලිතයකි. 
මෙම චලනය ඇත්තෙන්ම ඉතා වේගවත්ය. උදාහරණයක් ලෙස, කාමර උෂ්ණත්වයේ ඇති ලෝහවල, ඉලෙක්ට්රොනික තාප චලිතයේ වේගය තත්පරයට කිලෝමීටර් සිය ගණනක අනුපිළිවෙලක් ඇත!
ඔබ මෙම අහඹු චලනය දෙස හොඳින් බැලුවහොත්, සෑම අංශුවකම චලනය වන දිශාව ඕනෑම මොහොතක අහඹු බව ඔබට පෙනී යනු ඇත. ඔබ මෙම අංශුවල ප්රවේග දෛශික එකතු කළහොත් ප්රතිඵලය පාහේ ශුන්ය වේ.
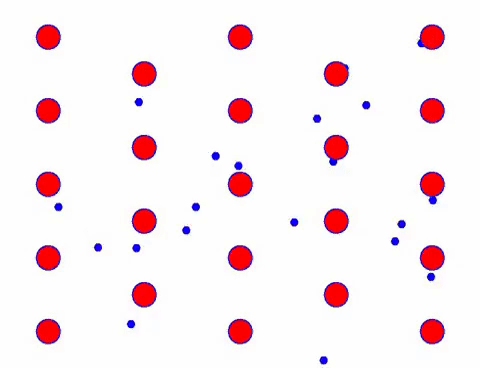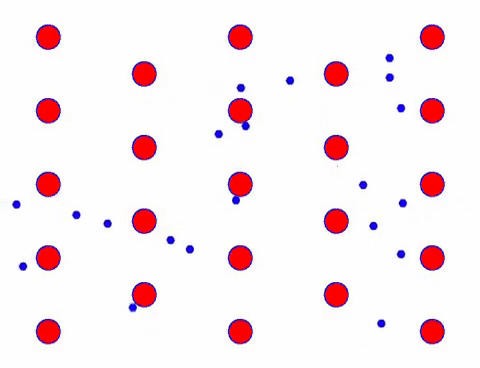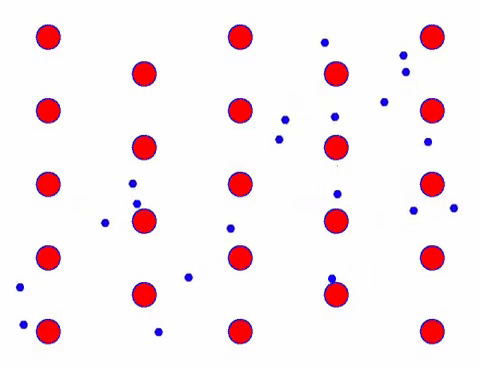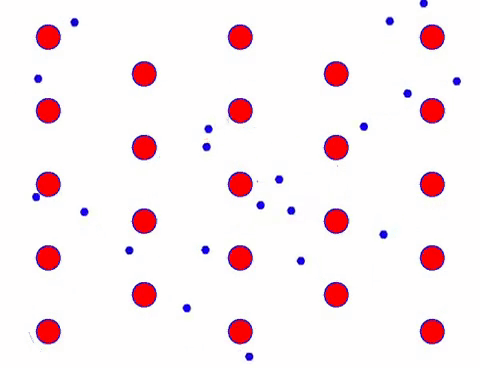
දැන් සන්නායකයට විද්යුත් ක්ෂේත්රයක් එකතු කරන්න, ඉලෙක්ට්රෝනය අහඹු චලනයේ පදනම මත දිශානුගත චලනයක් අධිස්ථාපනය කරයි. නිශ්චිත කාලයක් සඳහා විද්යුත් ක්ෂේත්රය වමට යැයි උපකල්පනය කළහොත්, ඉලෙක්ට්රෝන වල චලනය පහත පරිදි පෙනේ. රතු බෝල මගින් ස්ඵටික දැලිස් මත ඇති ලෝහ පරමාණු නියෝජනය කරන අතර වේගයෙන් චලනය වන තිත් නිදහස් ඉලෙක්ට්රෝන නියෝජනය කරයි. 
එය වේගයෙන් පෙනෙනවාද? එයට හේතුව ඉලෙක්ට්රොනික චලනය ඇත්තෙන්ම වේගවත් වීමයි! නමුත් ඇත්ත වශයෙන්ම, එහි විශාල කොටසක් සඳහා වන අහඹු චලනය, ධාරාව සඳහා දායක නොවේ. අහඹු චලිතය ඉවත් කළ විට, ඉතිරිය පහත මන්දගාමී පෙනුම මෙන් වේ.
ඇත්ත වශයෙන්ම, ඉලෙක්ට්රෝනවල දිශානුගත චලනය තාප චලිතයේ වේගයට වඩා බෙහෙවින් අඩුය. ඉලෙක්ට්රෝන වල මෙම “ඇඹරුම්” චලනය ප්ලාවිතය හෝ “ප්ලාවිතය” ලෙස හැඳින්වේ. සමහර විට, පරමාණු සමඟ ගැටීම නිසා ඉලෙක්ට්රෝන ප්රතිවිරුද්ධ දිශාවට ධාවනය වේ. නමුත් සාමාන්යයෙන් ඉලෙක්ට්රෝන එක් දිශාවකට ගමන් කරයි.
විද්යුත් ක්ෂේත්රය දිශාව වෙනස් වුවහොත් ඉලෙක්ට්රෝන ප්ලාවිතයේ දිශාව ද වෙනස් වේ.
එබැවින්, මෙම ආකාරයේ දිශානුගත චලනයකින් අදහස් වන්නේ යම් නිශ්චිත කාලයකදී සන්නායකතාවයට සහභාගී වන සියලුම ඉලෙක්ට්රෝනවල වේගයේ එකතුව ශුන්ය නොවන නමුත් සාමාන්යයෙන් නිශ්චිත දිශාවකටය. මෙම දිශාව ඕනෑම අවස්ථාවක වෙනස් කළ හැකි අතර, එය ප්රත්යාවර්ත ධාරාවකි.
එබැවින්, ධාරාව යනු විද්යුත් ආරෝපණයේ “සාමූහික චලිතය” වන බැවින් විද්යුත් ආරෝපණයේ “දිශා චලිතය” නොවේ.
සන්නායකයේ ධාරාවෙහි විශාලත්වය වත්මන් තීව්රතාවයෙන් ප්රකාශ වේ. ධාරා තීව්රතාවය යනු ඒකක කාලයකදී සන්නායකයේ හරස්කඩ හරහා ගමන් කරන විදුලි ප්රමාණය ලෙස අර්ථ දැක්වේ.
විද්යුත් ක්ෂේත්ර තීව්රතාවය සහ චුම්භක ප්රේරණ තීව්රතාවය වැනි “තීව්රතාවය” යන වචනය අඩංගු භෞතික ප්රමාණ කිහිපයක් අපි ඉගෙන ගෙන ඇත්තෙමු. ඒවා සාමාන්යයෙන් නියෝජනය කරන්නේ ඒකක කාලය, ඒකක ප්රදේශය (හෝ ඒකක පරිමාව, ඒකක ඝන කෝණය) අනුව බෙදීමයි. කෙසේ වෙතත්, වත්මන් තීව්රතාවයේ “තීව්රතාවය” යන වචනය ප්රදේශයේ වත්මන් බෙදීම පිළිබිඹු නොකරයි.
ඇත්ත වශයෙන්ම, වත්මන් ඝනත්වය වන ප්රදේශයට ධාරාව බෙදා හැරීම සඳහා තවත් භෞතික ප්රමාණයක් වගකිව යුතුය.
විද්යුත් ධාරාවේ සාරය විද්යුත් ආරෝපණයේ දිශානුගත චලනය වන බැවින්, වත්මන් තීව්රතාවය සහ ප්ලාවිත වේගය අතර යම් සම්බන්ධයක් තිබිය යුතුය!
මෙම සම්බන්ධතාවය ලබා ගැනීම සඳහා, අපි පළමුව සංකල්ප-වාහක සාන්ද්රණයක් පැහැදිලි කළ යුතුය, එනම්, ඒකක පරිමාවක වාහක ගණන, එය මගින් ප්රකාශ වේ.
සන්නායක හරස්කඩ, වාහක සාන්ද්රණය, ප්ලාවිත ප්රවේගය සහ ආරෝපිත ආරෝපණය යැයි උපකල්පනය කෙරේ.
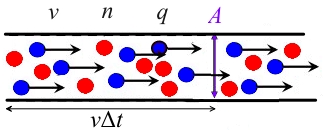
එවිට මතුපිට වම් පැත්තේ ඇති සන්නායකයේ ආරෝපණය වන අතර, මෙම ආරෝපණ යම් කාල සීමාවක් තුළ පෘෂ්ඨය හරහා ගමන් කරයි, එසේ
මෙය වත්මන් තීව්රතාවයේ අන්වීක්ෂීය ප්රකාශනයකි.
ධාරා ඝනත්වය යනු ධාරාව ප්රදේශයට බෙදීමයි, එබැවින් ධාරා ඝණත්වයේ විශාලත්වය යනු, නමුත් එය දෛශිකයක් ලෙස අර්ථ දක්වා ඇති අතර, දිශාව ධන ආරෝපිත වාහකවල ප්ලාවිත ප්රවේග දෛශිකයේ දිශාව වන අතර, එබැවින් ඉලෙක්ට්රෝන ප්ලාවිතය පහත උදාහරණයක් ලෙස මෙම ස්පීඩ් එකෙන් ලෝහ ලබා ගත හැක.
සෑම තඹ පරමාණුවක්ම වාහකයක් ලෙස ඉලෙක්ට්රෝනයක් දායක වේ යැයි උපකල්පනය කරමින් තඹ කම්බියක් සලකා බලන්න. තඹ මෝල් 1 ක් ඇත, එහි පරිමාව, මවුල ස්කන්ධය, ඝනත්වය, එවිට තඹ කම්බියේ වාහක සාන්ද්රණය වේ.
Avogadro ගේ නියතය කොහෙද. තඹ ඝනත්වය සොයා ගන්නා අතර, ආදේශ කිරීමෙන් ලැබෙන අගය ඒකක/ඝන මීටරයක් පමණ වේ.
තඹ කම්බියේ අරය 0.8mm යැයි උපකල්පනය කළහොත්, ගලා යන ධාරාව 15A, =1.6 C වන අතර ඉලෙක්ට්රෝනවල ප්ලාවිත ප්රවේගය ගණනය කරනු ලබන්නේ
ඉලෙක්ට්රෝනවල ප්ලාවිත වේගය ඇත්තෙන්ම ඉතා කුඩා බව දැකිය හැක.
පරිපථ අධ්යයනය කරන අය සඳහා, ඉහත දැක්වෙන්නේ ධාරාව පිළිබඳ සම්පූර්ණ අර්ථ දැක්වීමයි.
නමුත් භෞතික විද්යාවේදී ධාරාව පිළිබඳ ඉහත නිර්වචනය ඇත්ත වශයෙන්ම පටු නිර්වචනයක් පමණි. විද්යුත් ආරෝපණවල චලනය ධාරාව පවතින තාක් දුරට වඩා සාමාන්ය ධාරා සන්නායකවලට සීමා නොවේ. උදාහරණයක් ලෙස, හයිඩ්රජන් පරමාණුවක ඉලෙක්ට්රෝන න්යෂ්ටිය වටා ගමන් කරන විට එහි කක්ෂයේ විද්යුත් ධාරාවක් සෑදේ.

ඉලෙක්ට්රොනික ආරෝපණ ප්රමාණය සහ චලනය වන කාලය යැයි සිතමු. එවිට ගතවන සෑම අවස්ථාවකම ලූපයේ ඕනෑම හරස්කඩක් හරහා මෙතරම් විශාල ආරෝපණ ප්රමාණයක් ගමන් කරයි, එබැවින් වත්මන් තීව්රතාවය කාල සීමාව, සංඛ්යාතය සහ කෝණික ප්රවේගය අතර සම්බන්ධතාවය මත පදනම් වන අතර ධාරාව මෙසේ ද ප්රකාශ කළ හැකිය.
තවත් උදාහරණයක් ලෙස, ආරෝපිත ලෝහ තැටියක්, එහි අක්ෂය වටා භ්රමණය වන අතර, විවිධ අරය සහිත ලූප් ධාරා ද සාදයි.

මෙවැනි ධාරාවක් සාමාන්ය සන්නායක ධාරාවක් නොවන අතර ජූල් තාපය ජනනය කළ නොහැක! සැබෑ පරිපථයක් සෑදිය නොහැක.
එසේ නොමැතිනම්, හයිඩ්රජන් පරමාණුවේ ඉලෙක්ට්රෝන මගින් තත්පරයකට ජූල් තාපය කොපමණ ප්රමාණයක් ජනනය වේදැයි ගණනය කිරීමක් ඔබ මට දෙනවද?
ඇත්ත වශයෙන්ම, රික්තයේ ධාරාව ඕම්ගේ නියමය තෘප්තිමත් නොවේ. මක්නිසාද යත්, රික්තයේ ආරෝපිත අංශු චලනය වීමෙන් සාදන ලද විද්යුත් ධාරාව සඳහා, වාහක ලෝහයේ දැලිසට සමානව ගැටෙන්නේ නැති නිසා රික්තයට ප්රතිරෝධයක් සහ සන්නායකතාවයක් නොමැත.
විද්යුත් ආරෝපණ චලනය මගින් විද්යුත් ධාරාව ජනනය වන අතර විද්යුත් ආරෝපණය විද්යුත් ක්ෂේත්රය උද්දීපනය කරයි. මෙය වැරදි වැටහීමක් ඇති කිරීම පහසුය. එබැවින් බොහෝ අය සිතන්නේ විද්යුත් ධාරාව සාදන ආරෝපිත අංශුවල විද්යුත් ක්ෂේත්රය නිරාවරණය විය යුතු බවයි. නමුත් ඇත්ත වශයෙන්ම, සාමාන්ය සන්නායකයක සන්නායක ධාරාව සඳහා, ධන ආරෝපිත ලෝහ අයන විශාල සංඛ්යාවකින් සමන්විත පසුබිමක් මත වාහක ගලා යන අතර සන්නායකයම මධ්යස්ථ වේ!
අපි බොහෝ විට මෙවැනි විශේෂ ධාරාවක් “සමාන ධාරාවක්” ලෙස හඳුන්වමු. මෙහි සමානය යන්නෙන් අදහස් කරන්නේ එය සාමාන්ය සන්නායක ධාරාවක් මෙන් ම චුම්භක ක්ෂේත්රයක් ජනනය කරන බවයි!
මතක් කිරීම: මෙහි ඇති “සමාන ධාරාව” පරිපථ විශ්ලේෂණයේ “සමාන පරිපථය” සමඟ පටලවා නොගන්න.
ඇත්ත වශයෙන්ම, අපි මුලින්ම චුම්බක ක්ෂේත්රය අධ්යයනය කරන විට, Biot-Saffar ගේ නියමයේ විද්යුත් ධාරාව මෙම සමාන ධාරාව අඩංගු සාමාන්යකරණය වූ විද්යුත් ධාරාවයි. ඇත්ත වශයෙන්ම, මැක්ස්වෙල්ගේ සමීකරණවල සන්නායක ධාරාව සාමාන්යකරණය වූ ධාරාවට ද යොමු වේ.
ප්රකාශ විද්යුත් ආචරණය අධ්යයනය කළ අය දන්නවා ප්රකාශ ඉලෙක්ට්රෝනය කැතෝඩයේ සිට ඇනෝඩයට පාවෙන විට වාතයේ බලපෑම නොසලකා හරින්නේ නම්, මෙම ධාරාව රික්තයේ විද්යුත් ආරෝපණ චලනය වීම නිසා ඇති වන අතර ප්රතිරෝධයක් නොමැති බැවින් එය ඕම්ගේ නියමයෙන් සීමා නොවේ.
ඉතින්, භෞතික විද්යාවේ විද්යුත් ධාරාව පිළිබඳ එකම දෙය මෙයද?
නැත! චුම්භක ධාරාව සහ විස්ථාපන ධාරාව ලෙස වර්ග දෙකක් ද ඇත.
ඒවා ද සමාන ධාරා දෙකක් වන අතර, නමට අනුව, චුම්භකත්වය පැහැදිලි කිරීම සඳහා ද හඳුන්වා දෙනු ලැබේ. වෙනත් වචන වලින් කිවහොත්, ඔවුන් වත්මන් “ආරෝපණ චලනය” හි මූලික ලක්ෂණයෙන් කැඩී ඇත!
ඒක පුදුමයි! විද්යුත් ආරෝපණ චලනයක් නොමැත, එසේ නම් එය විද්යුත් ධාරාවක් ලෙස හැඳින්විය හැක්කේ ඇයි?
කලබල වෙන්න එපා, මම කියන දේ හෙමින් අහන්න.
අපි මුලින්ම චුම්භක ධාරාව බලමු.
චුම්භකත්වය විදුලිය චලනය වීම නිසා ඇති වන බව සොයා ගන්නා ලදී. ස්වභාවික චුම්භකත්වය පැහැදිලි කිරීම සඳහා, ප්රංශ භෞතික විද්යාඥ ඇම්පියර් “අණුක සංසරණය” පිළිබඳ උපකල්පනය ඉදිරිපත් කළේය. 
පහත රූපයේ දැක්වෙන පරිදි, ඕනෑම පරමාණුවක් හෝ අණුවක් කේන්ද්රය වටා භ්රමණය වන විද්යුත් ආරෝපණයක් ලෙස සැලකිය හැකිය, කුඩා ලූප් ධාරාවක් සාදයි, එනම් “අණුක සංසරණය”.
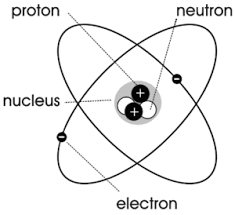
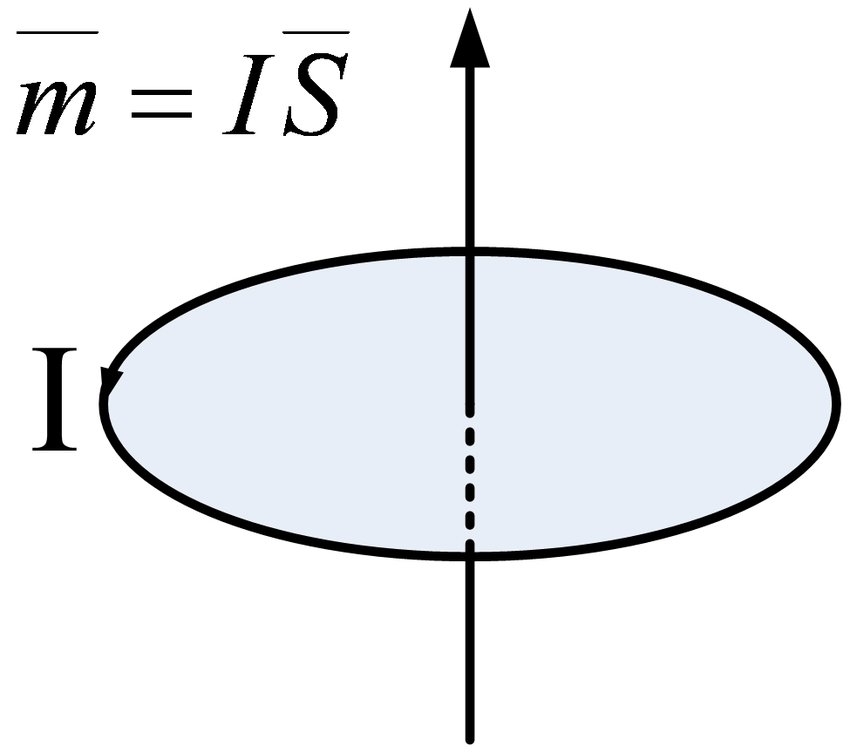
විද්යුත් ධාරාව චුම්භක ක්ෂේත්රය උද්දීපනය කරන නීතියට අනුව, මෙම අණුක සංසරණය චුම්භක මොහොත ලෙස හැඳින්වෙන භෞතික ප්රමාණයක් නිපදවනු ඇත. එහි විශාලත්වය යනු අණුක සංසරණ ධාරාවේ සමාන ධාරාවකින් ගුණ කරන ලද අණුක සංසරණ ප්රදේශය වන අතර එහි දිශාව සංසරණ දිශාව සමඟ දකුණු අත සර්පිලාකාර සම්බන්ධතාවයක පවතී, එනම්.
නිසැකවම, චුම්බක මොහොතේ දිශාව හරියටම සංසරණ ධාරාව මගින් සාදන ලද චුම්බක ක්ෂේත්රයේ දිශාව ඔස්සේ වේ.
. 
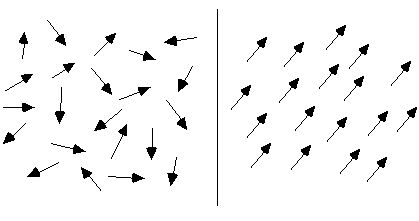
සාමාන්ය තත්ත්වයන් යටතේ, යම් ද්රව්යයක අණුක සංසරණ සැකැස්ම අවුල් සහගත බැවින් එම ද්රව්යය චුම්බක නොවේ, පහත රූපයේ වම් පැත්තේ පෙන්වා ඇත. බාහිර චුම්බක ක්ෂේත්රයකට යටත් වූ විට, මෙම අණුක සංසරණ ආසන්න වශයෙන් පිළිවෙලට සකස් කරනු ලැබේ. පහත රූපයේ දකුණු පැත්තේ පෙන්වා ඇති පරිදි, ඒවායේ චුම්බක අවස්ථාවන් හැකිතාක් එක් දිශාවකට සකස් කර ඇත, අසංඛ්යාත කුඩා චුම්බක ඉඳිකටු එකට එකතු වී සම්පූර්ණ චුම්බක ක්ෂේත්රයක් සාදනු ලබන අතර, ඒවායින් සමන්විත සම්පූර්ණ ද්රව්ය චුම්භක වේ.
සිලින්ඩරාකාර චුම්බකයක් ඇතැයි සිතමු, අභ්යන්තර අණුක සංසරණය මනාව සකසා ඇති අතර, චුම්බක කොටසේ කෙළවරේ ඇති එක් එක් අණුක සංසරණ කොටස් එකට සම්බන්ධ වී පහත රූපයේ පරිදි විශාල සංසරණයක් ඇති කරයි. 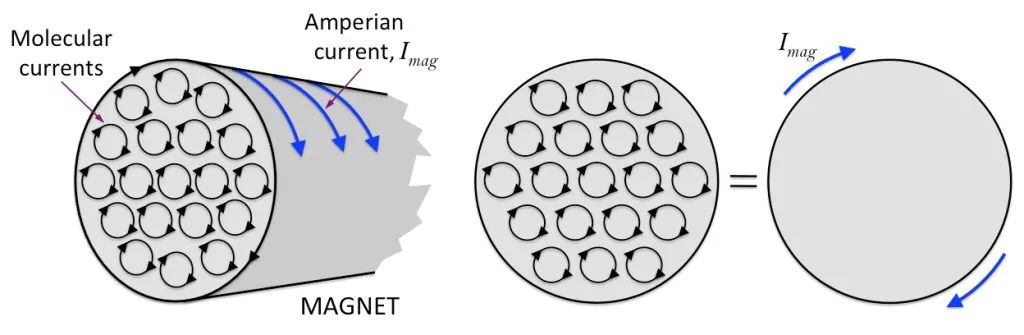
මේ මත පදනම්ව, තීරු චුම්බකයක් ශක්තිජනක විද්යුත් චුම්භකයක් වැනි යැයි අපට සිතිය හැකිය. වෙනත් වචන වලින් කිවහොත්, චුම්බකයේ මතුපිටට නොපෙනෙන ධාරාවක් පැටලී තිබේ! එවැනි ධාරාවක් සම්බන්ධ කර භාවිතා කළ නොහැක. එය චුම්බකයේ මතුපිටට සීමා වේ. අපි එය “බන්ධන ධාරාව” හෝ “චුම්බක ධාරාව” ලෙස හඳුන්වමු.
එබැවින්, චුම්භක ධාරාව යනු ධාරාවකි, මන්ද එය චුම්බක ක්ෂේත්රයක් සමාන ලෙස ජනනය කළ හැකි සැබෑ විද්යුත් ආරෝපණ චලනය මගින් සාදන ලද ධාරාවට සමාන වන බැවිනි!
අපි නැවතත් විස්ථාපන ධාරාව දෙස බලමු.
Ampere’s loop theorem එකට අනුව, සංවෘත මාර්ගයක ඇති චුම්බක ක්ෂේත්ර ශක්තියේ අනුකලනය, මෙම මාර්ගයෙන් සීමා වූ ඕනෑම වක්ර පෘෂ්ඨයක් මත පවතින ධාරා ඝනත්වයේ ප්රවාහයට සමාන වේ, එනම් මෙම ප්රමේයය ගණිතයේ දී Stokes’ theorem ලෙස හැඳින්වේ. එය අපට පවසන්නේ ඕනෑම සංවෘත මාර්ගයක් ඔස්සේ දෛශිකයක අනුකලනය සංවෘත මාර්ගයෙන් සීමා වූ ඕනෑම මතුපිටකට එහි curl (මෙහි) ප්රවාහයට සමාන විය යුතු බවයි.
එය ගණිතමය ප්රමේයයක් බැවින් එය සැමවිටම නිවැරදි විය යුතුය, මන්ද ගණිතය යනු ප්රත්යක්ෂ මත පදනම් වූ තාර්කික පද්ධතියකි.
එබැවින්, ඇම්පියර් ලූප් ප්රමේයය සැමවිටම පැවතිය යුතුය!
කෙසේ වෙතත්, දක්ෂ ස්කොට්ලන්ත භෞතික විද්යාඥ මැක්ස්වෙල් විසින් අස්ථායී ධාරා පරිපථයකට මුහුණ දෙන විට, ඇම්පියර් ලූප් ප්රමේයය පරස්පර විරෝධී බව සොයා ගන්නා ලදී.

සාමාන්ය අස්ථායී ධාරාව ධාරිත්රකයේ ආරෝපණය සහ විසර්ජනය අතරතුර සිදු වේ. පහත රූපයේ දැක්වෙන පරිදි, ධාරිත්රකය ආරෝපණය කිරීමේ කෙටි කාලය තුළ අස්ථායී ධාරාවක් පවතී.
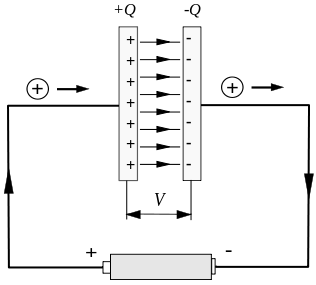
නමුත් ධාරිත්රක තහඩු අතර පරිපථය විසන්ධි වී ඇති අතර එය බරපතල ගැටළුවක් ඇති කරයි.
පහත රූපයේ දැක්වෙන පරිදි වයරය මග හරින සංවෘත මාර්ගයක් අපි සලකමු, C මගින් සලකුණු කර ඇති රවුම සහ එය මායිම ලෙස වක්ර මතුපිට අත්තනෝමතික ලෙස තෝරා ගත හැකිය. රූපයේ, C විසින්ම සහ ධාරිත්රකය හරහා වට කර ඇති රවුම් තලය තෝරා ඇත. වම් තහඩුවේ වක්ර මතුපිට. 
වෘත්තාකාර පෘෂ්ඨයට අනුව, වක්ර පෘෂ්ඨයට අනුව, නමුත් චුම්බක ක්ෂේත්රයේ ශක්තියේ ලූප අනුකලනයක් ලෙස, එහි අගය තීරණය කළ යුතු බව දැකිය හැකිය!
කොහොමද කරන්නේ?
මැක්ස්වෙල් විශ්වාස කරන්නේ ඇම්පියර් ලූප් ප්රමේයය ස්ථාපිත කළ යුතු බවයි. දැන් ප්රශ්නයක් තියෙනවා, ඒ ධාරාවේ කොටසක් අප විසින් මීට පෙර සොයා නොගත් නමුත් එය පවතින නිසා විය යුතුය!
ඉතින්, ධාරාවෙහි මෙම කොටස සොයා ගන්නේ කෙසේද?
ගැටළුව තහඩු අතර ඇති බැවින්, තහඩු අතර සිට ආරම්භ කරන්න.
විශ්ලේෂණය හරහා, මැක්ස්වෙල් විසින් ආරෝපණය කිරීම හෝ විසර්ජනය කිරීම නොතකා, ධාරිත්රක තහඩු අතර සෑම විටම භෞතික ප්රමාණයක් පවතින අතර එය ධාරාවේ විශාලත්වය සහ දිශාව සමඟ සමමුහුර්ත වේ. එය විද්යුත් විස්ථාපන දෛශිකයේ ප්රවාහයේ කාල ව්යුත්පන්නය, එනම් එය විස්ථාපන ධාරාව ලෙස අර්ථ දැක්වේ.
මෙම කොටස මීට පෙර සොයා නොගත් ධාරාවේ කොටස යැයි සැලකේ නම්, සම්පූර්ණ ධාරාව දැන් වේ. එනම්, තහඩු අතර පරිපථය විසන්ධි වී ඇතත්, විද්යුත් විස්ථාපන ප්රවාහයේ ව්යුත්පන්නය සහ ධාරාවේ එකතුව, සමස්තයක් ලෙස, සෑම විටම ධාරාවේ අඛණ්ඩතාව සහතික කිරීම.
පෙර ප්රතිවිරෝධය වෙත ආපසු යමින්, අපි දැන් දන්නවා, ස්ටෝක්ස් ප්රමේයයේ අවශ්යතා අනුව, සංවෘත මතුපිටක් සඳහා ධාරා ඝනත්වයේ ප්රවාහය ගණනය කිරීමේදී, විස්ථාපන ධාරාවේ ඝනත්වය ද සලකා බැලිය යුතුය, එනම් සම්පූර්ණ ඇම්පියර් ලූපය ප්රමේයය යනු, මෙම නව වත්මන් සංරචකය “සොයාගැනීමෙන්”, Ampere Loop Theorem හි අර්බුදය විසඳනු ලැබේ!
මෙහි “හැඳින්වීම” භාවිතා නොකිරීමට හේතුව, නමුත් “සොයාගැනීම” මෙහි භාවිතා වේ. මට අවධාරණය කිරීමට අවශ්ය වන්නේ මෙවැනි ධාරාවක් ගණිතමය වන්දියක් නොව සැබෑ දෙයක් වන නමුත් එය මීට පෙර සොයාගෙන නොමැති බවයි.
එය මුලින්ම පවතින්නේ ඇයි? එය විදුලි ධාරාවක් ලෙස ක්රියා කරන නිසා, සන්නායක ධාරාවක් මෙන්, එය චුම්බක ක්ෂේත්රයක් සමානව උද්දීපනය කරයි, විද්යුත් ආරෝපණ චලනයක් නොමැති බව හැර, වයර් අවශ්ය නොවේ, ජූල් තාපය ජනනය කළ නොහැක, එබැවින් එය නොසලකා හැර ඇත!
නමුත් එය ඇත්ත වශයෙන්ම පවතින්නේ තනිවමයි, අඩු පැතිකඩක් තබා ගන්න, එය සෑම විටම එහි චුම්භක ක්ෂේත්රය නිශ්ශබ්දව උද්දීපනය කරයි!
වෙනත් වචන වලින් කිවහොත්, අපි චුම්බක ක්ෂේත්රයකට මුහුණ දෙන විට, ධාරාව පිළිබඳ මුල් අර්ථ දැක්වීම ඉතා පටු ය. විද්යුත් ධාරාවෙහි සාරය විද්යුත් ආරෝපණ චලනය නොවේ, එය චුම්බක ක්ෂේත්රයක් උද්දීපනය කළ හැකි දෙයක් විය යුතුය.
මේ වන විට ධාරාවේ ආකාර කිහිපයක් හඳුන්වා දී ඇත. ඒවා සියල්ලම වෛෂයිකව පවතින අතර, ඒවාට පොදුවේ ඇති දෙය නම්, සියලුම ධාරා චුම්භක ක්ෂේත්රය සමානව උද්දීපනය කළ හැකි බවයි.
