ವಿದ್ಯುತ್ ಪ್ರವಾಹ ಎಂದರೇನು? ಮೊದಲು ನೆನಪಿಸಿಕೊಳ್ಳಿ, ನಾವು ಕಲಿತ ಕರೆಂಟ್‌ನ ವ್ಯಾಖ್ಯಾನವೇನು?

ಸರಳವಾಗಿ, ಕಂಡಕ್ಟರ್ನಲ್ಲಿ ಚಾರ್ಜ್ಡ್ ಕಣಗಳ ದಿಕ್ಕಿನ ಚಲನೆಯು ವಿದ್ಯುತ್ ಪ್ರವಾಹವಾಗಿದೆ.

ವಸ್ತುವು ಮುಕ್ತವಾಗಿ ಚಲಿಸಬಲ್ಲ ಕಣಗಳನ್ನು ಚಾರ್ಜ್ ಮಾಡಿದಾಗ ಮಾತ್ರ, ಅದು ವಿದ್ಯುತ್ ಪ್ರವಾಹವನ್ನು ರವಾನಿಸುತ್ತದೆ-ಅಂದರೆ, ವಿದ್ಯುತ್ ಅನ್ನು ನಡೆಸುತ್ತದೆ. ವಹನದಲ್ಲಿ ಭಾಗವಹಿಸುವ ಈ ಚಾರ್ಜ್ಡ್ ಕಣಗಳನ್ನು ವಾಹಕಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಲೋಹಗಳಿಗೆ, ಉದಾಹರಣೆಗೆ, ಪರಮಾಣುಗಳ ಹೊರಗಿನ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳು ಮಾತ್ರ ವಾಹಕಗಳಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತವೆ.

ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ವ್ಯಾಖ್ಯಾನದಲ್ಲಿ “ದಿಕ್ಕಿನ ಚಲನೆ” ಸಾಮಾನ್ಯವಾಗಿ ತಪ್ಪಾಗಿ ಗ್ರಹಿಸಲ್ಪಡುತ್ತದೆ. ಇದು ಒಂದು ನಿರ್ದಿಷ್ಟ ದಿಕ್ಕಿನಲ್ಲಿ ಚಲನೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ ಎಂದು ಅನೇಕ ಜನರು ಭಾವಿಸುತ್ತಾರೆ, ಖಂಡಿತ ಅಲ್ಲ! ಎಸಿ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿನ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ಚಲನೆಯ ದಿಕ್ಕು ಬದಲಾಗುವುದಿಲ್ಲವೇ?

ವಾಸ್ತವವಾಗಿ, ಓರಿಯಂಟೀರಿಂಗ್ “ಯಾದೃಚ್ಛಿಕ ಚಲನೆ” ಗೆ ಸಂಬಂಧಿಸಿದೆ!

ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳು ಸೂಕ್ಷ್ಮ ಕಣಗಳಾಗಿರುವುದರಿಂದ, ಅವು ಎಲ್ಲಾ ಸಮಯದಲ್ಲೂ ಉಷ್ಣ ಚಲನೆಯಲ್ಲಿರಬೇಕು. ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ಉಷ್ಣ ಚಲನೆಯು ಯಾದೃಚ್ಛಿಕ ಚಲನೆಯಾಗಿದೆ.

ಈ ಚಲನೆಯು ವಾಸ್ತವವಾಗಿ ತುಂಬಾ ವೇಗವಾಗಿರುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಕೋಣೆಯ ಉಷ್ಣಾಂಶದಲ್ಲಿ ಲೋಹಗಳಲ್ಲಿ, ಎಲೆಕ್ಟ್ರಾನಿಕ್ ಥರ್ಮಲ್ ಚಲನೆಯ ವೇಗವು ಸೆಕೆಂಡಿಗೆ ನೂರಾರು ಕಿಲೋಮೀಟರ್ಗಳ ಕ್ರಮದಲ್ಲಿದೆ!

ಈ ಯಾದೃಚ್ಛಿಕ ಚಲನೆಯನ್ನು ನೀವು ಹತ್ತಿರದಿಂದ ನೋಡಿದರೆ, ಪ್ರತಿಯೊಂದು ಕಣದ ಚಲನೆಯ ದಿಕ್ಕು ಯಾವುದೇ ಕ್ಷಣದಲ್ಲಿ ಯಾದೃಚ್ಛಿಕವಾಗಿರುತ್ತದೆ ಎಂದು ನೀವು ಕಂಡುಕೊಳ್ಳುತ್ತೀರಿ. ಈ ಕಣಗಳ ವೇಗ ವಾಹಕಗಳನ್ನು ನೀವು ಸೇರಿಸಿದರೆ, ಫಲಿತಾಂಶವು ಬಹುತೇಕ ಶೂನ್ಯವಾಗಿರುತ್ತದೆ.

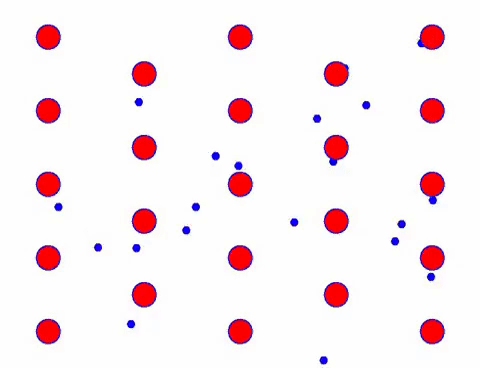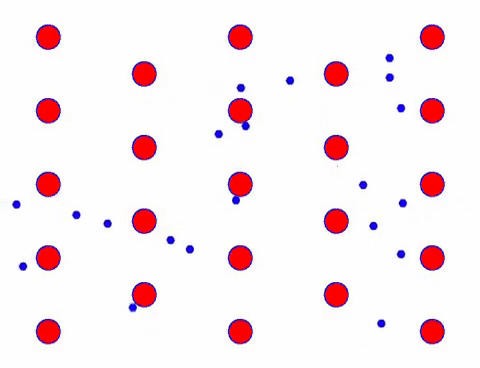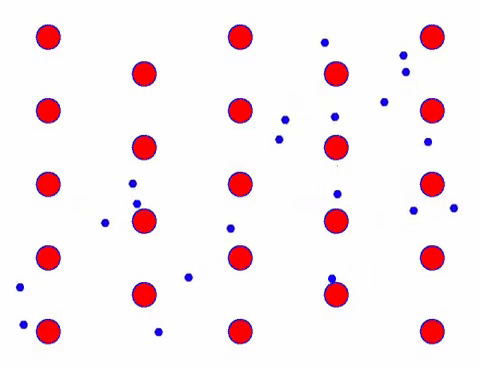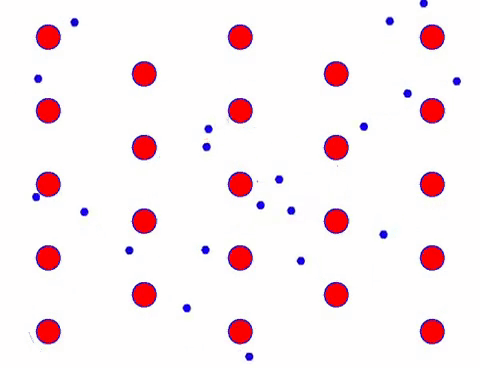
ಈಗ ವಾಹಕಕ್ಕೆ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವನ್ನು ಸೇರಿಸಿ, ಮತ್ತು ಎಲೆಕ್ಟ್ರಾನ್ ಯಾದೃಚ್ಛಿಕ ಚಲನೆಯ ಆಧಾರದ ಮೇಲೆ ದಿಕ್ಕಿನ ಚಲನೆಯನ್ನು ಅತಿಕ್ರಮಿಸುತ್ತದೆ. ಒಂದು ನಿರ್ದಿಷ್ಟ ಅವಧಿಗೆ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವು ಎಡಕ್ಕೆ ಎಂದು ಊಹಿಸಿ, ಎಲೆಕ್ಟ್ರಾನ್ಗಳ ಚಲನೆಯು ಈ ಕೆಳಗಿನಂತೆ ಕಾಣುತ್ತದೆ. ಕೆಂಪು ಚೆಂಡುಗಳು ಸ್ಫಟಿಕ ಜಾಲರಿಯಲ್ಲಿ ಲೋಹದ ಪರಮಾಣುಗಳನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತವೆ ಮತ್ತು ವೇಗವಾಗಿ ಚಲಿಸುವ ಚುಕ್ಕೆಗಳು ಮುಕ್ತ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತವೆ.

ಇದು ವೇಗವಾಗಿ ಕಾಣುತ್ತದೆಯೇ? ಏಕೆಂದರೆ ಎಲೆಕ್ಟ್ರಾನಿಕ್ ಚಲನೆಯು ನಿಜವಾಗಿಯೂ ವೇಗವಾಗಿರುತ್ತದೆ! ಆದರೆ ವಾಸ್ತವವಾಗಿ, ಯಾದೃಚ್ಛಿಕ ಚಲನೆಯು, ಅದರಲ್ಲಿ ಹೆಚ್ಚಿನ ಪ್ರಮಾಣವನ್ನು ಹೊಂದಿದೆ, ಇದು ಪ್ರಸ್ತುತಕ್ಕೆ ಕೊಡುಗೆ ನೀಡುವುದಿಲ್ಲ. ಯಾದೃಚ್ಛಿಕ ಚಲನೆಯನ್ನು ತೆಗೆದುಹಾಕಿದಾಗ, ಉಳಿದವು ಕೆಳಗಿರುವ ನಿಧಾನ ನೋಟದಂತೆಯೇ ಇರುತ್ತದೆ.

ವಾಸ್ತವವಾಗಿ, ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ದಿಕ್ಕಿನ ಚಲನೆಯು ಉಷ್ಣ ಚಲನೆಯ ವೇಗಕ್ಕಿಂತ ಹೆಚ್ಚು ನಿಧಾನವಾಗಿರುತ್ತದೆ. ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ಈ “ಗ್ರೈಂಡಿಂಗ್” ಚಲನೆಯನ್ನು ಡ್ರಿಫ್ಟ್ ಅಥವಾ “ಡ್ರಿಫ್ಟ್” ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಕೆಲವೊಮ್ಮೆ, ಪರಮಾಣುಗಳೊಂದಿಗೆ ಘರ್ಷಣೆಯಿಂದಾಗಿ ಎಲೆಕ್ಟ್ರಾನ್ಗಳು ವಿರುದ್ಧ ದಿಕ್ಕಿನಲ್ಲಿ ಚಲಿಸುತ್ತವೆ. ಆದರೆ ಸಾಮಾನ್ಯವಾಗಿ, ಎಲೆಕ್ಟ್ರಾನ್ಗಳು ಒಂದು ದಿಕ್ಕಿನಲ್ಲಿ ಚಲಿಸುತ್ತವೆ.

ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವು ದಿಕ್ಕನ್ನು ಬದಲಾಯಿಸಿದರೆ, ಎಲೆಕ್ಟ್ರಾನ್ ಡ್ರಿಫ್ಟ್‌ನ ದಿಕ್ಕು ಕೂಡ ಬದಲಾಗುತ್ತದೆ.

ಆದ್ದರಿಂದ, ಈ ರೀತಿಯ ದಿಕ್ಕಿನ ಚಲನೆ ಎಂದರೆ ಒಂದು ನಿರ್ದಿಷ್ಟ ಸಮಯದಲ್ಲಿ ವಹನದಲ್ಲಿ ಭಾಗವಹಿಸುವ ಎಲ್ಲಾ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ವೇಗದ ಮೊತ್ತವು ಶೂನ್ಯವಾಗಿರುವುದಿಲ್ಲ, ಆದರೆ ಸಾಮಾನ್ಯವಾಗಿ ಒಂದು ನಿರ್ದಿಷ್ಟ ದಿಕ್ಕಿನಲ್ಲಿದೆ. ಈ ದಿಕ್ಕನ್ನು ಯಾವುದೇ ಸಮಯದಲ್ಲಿ ಬದಲಾಯಿಸಬಹುದು, ಮತ್ತು ಅದು ಪರ್ಯಾಯ ಪ್ರವಾಹದ ಸಂದರ್ಭವಾಗಿದೆ.

ಆದ್ದರಿಂದ, ಪ್ರಸ್ತುತವು ವಿದ್ಯುದಾವೇಶದ “ಸಾಮೂಹಿಕ ಚಲನೆ” ಆಗಿರುವುದರಿಂದ ವಿದ್ಯುದಾವೇಶದ “ದಿಕ್ಕಿನ ಚಲನೆ” ಅಲ್ಲ.

ವಾಹಕದಲ್ಲಿನ ಪ್ರವಾಹದ ಪ್ರಮಾಣವು ಪ್ರಸ್ತುತ ತೀವ್ರತೆಯಿಂದ ವ್ಯಕ್ತವಾಗುತ್ತದೆ. ಪ್ರಸ್ತುತ ತೀವ್ರತೆಯನ್ನು ಒಂದು ಘಟಕದ ಸಮಯದಲ್ಲಿ ವಾಹಕದ ಅಡ್ಡ-ವಿಭಾಗದ ಮೂಲಕ ಹಾದುಹೋಗುವ ವಿದ್ಯುತ್ ಪ್ರಮಾಣ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ, ಅವುಗಳೆಂದರೆ

ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ತೀವ್ರತೆ ಮತ್ತು ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ತೀವ್ರತೆಯಂತಹ “ತೀವ್ರತೆ” ಪದವನ್ನು ಒಳಗೊಂಡಿರುವ ಕೆಲವು ಭೌತಿಕ ಪ್ರಮಾಣಗಳನ್ನು ನಾವು ಕಲಿತಿದ್ದೇವೆ. ಅವು ಸಾಮಾನ್ಯವಾಗಿ ಪ್ರತಿ ಯುನಿಟ್ ಸಮಯ, ಯುನಿಟ್ ಪ್ರದೇಶ (ಅಥವಾ ಯುನಿಟ್ ಪರಿಮಾಣ, ಘಟಕ ಘನ ಕೋನ) ಪ್ರತಿ ಹಂಚಿಕೆಯನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತವೆ. ಆದಾಗ್ಯೂ, ಪ್ರಸ್ತುತ ತೀವ್ರತೆಯಲ್ಲಿ “ತೀವ್ರತೆ” ಎಂಬ ಪದವು ಪ್ರದೇಶದ ಪ್ರಸ್ತುತ ಹಂಚಿಕೆಯನ್ನು ಪ್ರತಿಬಿಂಬಿಸುವುದಿಲ್ಲ.

ವಾಸ್ತವವಾಗಿ, ಮತ್ತೊಂದು ಭೌತಿಕ ಪ್ರಮಾಣವು ಪ್ರದೇಶಕ್ಕೆ ಪ್ರವಾಹದ ವಿತರಣೆಗೆ ಕಾರಣವಾಗಿದೆ, ಇದು ಪ್ರಸ್ತುತ ಸಾಂದ್ರತೆಯಾಗಿದೆ.

ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಸಾರವು ವಿದ್ಯುದಾವೇಶದ ದಿಕ್ಕಿನ ಚಲನೆಯಾಗಿರುವುದರಿಂದ, ಪ್ರಸ್ತುತ ತೀವ್ರತೆ ಮತ್ತು ಡ್ರಿಫ್ಟ್ ವೇಗದ ನಡುವೆ ಒಂದು ನಿರ್ದಿಷ್ಟ ಸಂಬಂಧವಿರಬೇಕು!

ಈ ಸಂಬಂಧವನ್ನು ಪಡೆಯಲು, ನಾವು ಮೊದಲು ಪರಿಕಲ್ಪನೆ-ವಾಹಕ ಸಾಂದ್ರತೆಯನ್ನು ಸ್ಪಷ್ಟಪಡಿಸಬೇಕು, ಅಂದರೆ, ಒಂದು ಘಟಕದ ಪರಿಮಾಣದಲ್ಲಿನ ವಾಹಕಗಳ ಸಂಖ್ಯೆ, ಇದನ್ನು  ಮೂಲಕ ವ್ಯಕ್ತಪಡಿಸಲಾಗುತ್ತದೆ.

ಕಂಡಕ್ಟರ್ ಕ್ರಾಸ್ ಸೆಕ್ಷನ್, ಕ್ಯಾರಿಯರ್ ಸಾಂದ್ರತೆ, ಡ್ರಿಫ್ಟ್ ವೇಗ ಮತ್ತು ಚಾರ್ಜ್ಡ್ ಚಾರ್ಜ್ ಎಂದು ಊಹಿಸಲಾಗಿದೆ.

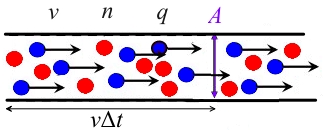
ನಂತರ ಮೇಲ್ಮೈಯ ಎಡಭಾಗದಲ್ಲಿರುವ ವಾಹಕದಲ್ಲಿನ ಚಾರ್ಜ್ ಆಗಿರುತ್ತದೆ ಮತ್ತು ಈ ಶುಲ್ಕಗಳು ಒಂದು ನಿರ್ದಿಷ್ಟ ಅವಧಿಯೊಳಗೆ ಮೇಲ್ಮೈ ಮೂಲಕ ಹಾದು ಹೋಗುತ್ತವೆ, ಆದ್ದರಿಂದ

ಇದು ಪ್ರಸ್ತುತ ತೀವ್ರತೆಯ ಸೂಕ್ಷ್ಮ ಅಭಿವ್ಯಕ್ತಿಯಾಗಿದೆ.

ಪ್ರಸ್ತುತ ಸಾಂದ್ರತೆಯು ಪ್ರದೇಶಕ್ಕೆ ಪ್ರವಾಹದ ಹಂಚಿಕೆಯಾಗಿದೆ, ಆದ್ದರಿಂದ ಪ್ರಸ್ತುತ ಸಾಂದ್ರತೆಯ ಪ್ರಮಾಣ, ಆದರೆ ಅದನ್ನು ವೆಕ್ಟರ್ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ, ಮತ್ತು ದಿಕ್ಕು ಧನಾತ್ಮಕ ಆವೇಶದ ವಾಹಕಗಳ ಡ್ರಿಫ್ಟ್ ವೇಗ ವೆಕ್ಟರ್‌ನ ದಿಕ್ಕು, ಆದ್ದರಿಂದ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ಡ್ರಿಫ್ಟ್ ಕೆಳಗಿನ ಉದಾಹರಣೆಯಂತೆ ಈ ವೇಗದಿಂದ ಲೋಹವನ್ನು ಪಡೆಯಬಹುದು.

ತಾಮ್ರದ ತಂತಿಯನ್ನು ಪರಿಗಣಿಸಿ, ಪ್ರತಿ ತಾಮ್ರದ ಪರಮಾಣು ಎಲೆಕ್ಟ್ರಾನ್ ಅನ್ನು ವಾಹಕವಾಗಿ ಕೊಡುಗೆ ನೀಡುತ್ತದೆ ಎಂದು ಊಹಿಸಿ. ತಾಮ್ರದ 1 ಮೋಲ್ ಇದೆ, ಅದರ ಪರಿಮಾಣ, ಮೋಲಾರ್ ದ್ರವ್ಯರಾಶಿ, ಸಾಂದ್ರತೆ, ನಂತರ ತಾಮ್ರದ ತಂತಿಯ ವಾಹಕ ಸಾಂದ್ರತೆ

ಅವೊಗಾಡ್ರೊ ಸ್ಥಿರತೆ ಎಲ್ಲಿದೆ. ತಾಮ್ರದ ಸಾಂದ್ರತೆಯು ಕಂಡುಬರುತ್ತದೆ ಮತ್ತು ಬದಲಿಯಾಗಿ ಪಡೆದ ಮೌಲ್ಯವು ಸುಮಾರು ಯೂನಿಟ್/ಕ್ಯೂಬಿಕ್ ಮೀಟರ್ ಆಗಿದೆ.

ತಾಮ್ರದ ತಂತಿಯ ತ್ರಿಜ್ಯವು 0.8mm ಎಂದು ಊಹಿಸಿದರೆ, ಹರಿಯುವ ಪ್ರವಾಹವು 15A, =1.6 C, ಮತ್ತು ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ಡ್ರಿಫ್ಟ್ ವೇಗವನ್ನು ಹೀಗೆ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ

ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ಡ್ರಿಫ್ಟ್ ವೇಗವು ತುಂಬಾ ಚಿಕ್ಕದಾಗಿದೆ ಎಂದು ನೋಡಬಹುದು.

ಸರ್ಕ್ಯೂಟ್ಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡುವವರಿಗೆ, ಮೇಲಿನವು ಪ್ರಸ್ತುತದ ಸಂಪೂರ್ಣ ವ್ಯಾಖ್ಯಾನವಾಗಿದೆ.

ಆದರೆ ಭೌತಶಾಸ್ತ್ರದಲ್ಲಿ, ಪ್ರಸ್ತುತದ ಮೇಲಿನ ವ್ಯಾಖ್ಯಾನವು ವಾಸ್ತವವಾಗಿ ಕಿರಿದಾದ ವ್ಯಾಖ್ಯಾನವಾಗಿದೆ. ವಿದ್ಯುದಾವೇಶಗಳ ಚಲನೆಯು ಪ್ರಸ್ತುತವಾಗಿರುವವರೆಗೆ ಹೆಚ್ಚು ಸಾಮಾನ್ಯ ಪ್ರವಾಹಗಳು ವಾಹಕಗಳಿಗೆ ಸೀಮಿತವಾಗಿಲ್ಲ. ಉದಾಹರಣೆಗೆ, ಹೈಡ್ರೋಜನ್ ಪರಮಾಣುವಿನ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳು ನ್ಯೂಕ್ಲಿಯಸ್‌ನ ಸುತ್ತ ಚಲಿಸಿದಾಗ, ಅದರ ಕಕ್ಷೆಯಲ್ಲಿ ವಿದ್ಯುತ್ ಪ್ರವಾಹವು ರೂಪುಗೊಳ್ಳುತ್ತದೆ.

ಎಲೆಕ್ಟ್ರಾನಿಕ್ ಚಾರ್ಜ್ನ ಮೊತ್ತ ಮತ್ತು ಚಲನೆಯ ಅವಧಿ ಎಂದು ಭಾವಿಸೋಣ. ನಂತರ ಪ್ರತಿ ಬಾರಿ ಕಳೆದುಹೋದಾಗ, ಲೂಪ್ನ ಯಾವುದೇ ಅಡ್ಡ ವಿಭಾಗದ ಮೂಲಕ ಅಂತಹ ದೊಡ್ಡ ಪ್ರಮಾಣದ ಚಾರ್ಜ್ ಹಾದುಹೋಗುತ್ತದೆ, ಆದ್ದರಿಂದ ಪ್ರಸ್ತುತ ತೀವ್ರತೆಯು ಅವಧಿ, ಆವರ್ತನ ಮತ್ತು ಕೋನೀಯ ವೇಗದ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ಆಧರಿಸಿದೆ ಮತ್ತು ಪ್ರಸ್ತುತವನ್ನು ಹೀಗೆ ವ್ಯಕ್ತಪಡಿಸಬಹುದು

ಇನ್ನೊಂದು ಉದಾಹರಣೆಗಾಗಿ, ಚಾರ್ಜ್ಡ್ ಮೆಟಲ್ ಡಿಸ್ಕ್, ಅದರ ಅಕ್ಷದ ಸುತ್ತ ತಿರುಗುತ್ತದೆ, ವಿಭಿನ್ನ ತ್ರಿಜ್ಯಗಳೊಂದಿಗೆ ಲೂಪ್ ಪ್ರವಾಹಗಳನ್ನು ಸಹ ರೂಪಿಸುತ್ತದೆ.

ಈ ರೀತಿಯ ಪ್ರವಾಹವು ಸಾಮಾನ್ಯ ವಹನ ಪ್ರವಾಹವಲ್ಲ ಮತ್ತು ಜೌಲ್ ಶಾಖವನ್ನು ಉತ್ಪಾದಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ! ನಿಜವಾದ ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ರೂಪಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ.

ಇಲ್ಲದಿದ್ದರೆ, ಹೈಡ್ರೋಜನ್ ಪರಮಾಣುವಿನ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳಿಂದ ಸೆಕೆಂಡಿಗೆ ಎಷ್ಟು ಜೌಲ್ ಶಾಖವು ಉತ್ಪತ್ತಿಯಾಗುತ್ತದೆ ಎಂಬ ಲೆಕ್ಕಾಚಾರವನ್ನು ನೀವು ನನಗೆ ನೀಡುತ್ತೀರಾ?

ವಾಸ್ತವವಾಗಿ, ನಿರ್ವಾತದಲ್ಲಿನ ಪ್ರವಾಹವು ಓಮ್ನ ನಿಯಮವನ್ನು ಪೂರೈಸುವುದಿಲ್ಲ. ಏಕೆಂದರೆ, ನಿರ್ವಾತದಲ್ಲಿನ ವಿದ್ಯುದಾವೇಶದ ಕಣಗಳ ಚಲನೆಯಿಂದ ರೂಪುಗೊಂಡ ವಿದ್ಯುತ್ ಪ್ರವಾಹಕ್ಕೆ, ವಾಹಕಗಳು ಲೋಹದಲ್ಲಿನ ಜಾಲರಿಯಂತೆ ಡಿಕ್ಕಿಹೊಡೆಯುವುದಿಲ್ಲ, ಆದ್ದರಿಂದ ನಿರ್ವಾತವು ಯಾವುದೇ ಪ್ರತಿರೋಧ ಮತ್ತು ವಾಹಕತೆಯನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ.

ವಿದ್ಯುದಾವೇಶಗಳ ಚಲನೆಯು ವಿದ್ಯುತ್ ಪ್ರವಾಹವನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ, ಮತ್ತು ವಿದ್ಯುದಾವೇಶವು ಸ್ವತಃ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವನ್ನು ಪ್ರಚೋದಿಸುತ್ತದೆ. ಇದು ತಪ್ಪು ತಿಳುವಳಿಕೆಯನ್ನು ಉಂಟುಮಾಡುವುದು ಸುಲಭ. ಆದ್ದರಿಂದ ವಿದ್ಯುತ್ ಪ್ರವಾಹವನ್ನು ರೂಪಿಸುವ ಚಾರ್ಜ್ಡ್ ಕಣಗಳ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವನ್ನು ಬಹಿರಂಗಪಡಿಸಬೇಕು ಎಂದು ಅನೇಕ ಜನರು ಭಾವಿಸುತ್ತಾರೆ. ಆದರೆ ವಾಸ್ತವವಾಗಿ, ಸಾಮಾನ್ಯ ವಾಹಕದಲ್ಲಿನ ವಹನ ಪ್ರವಾಹಕ್ಕೆ, ವಾಹಕಗಳು ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ಧನಾತ್ಮಕ ಆವೇಶದ ಲೋಹದ ಅಯಾನುಗಳಿಂದ ಕೂಡಿದ ಹಿನ್ನೆಲೆಯಲ್ಲಿ ಹರಿಯುತ್ತವೆ ಮತ್ತು ಕಂಡಕ್ಟರ್ ಸ್ವತಃ ತಟಸ್ಥವಾಗಿದೆ!

ನಾವು ಸಾಮಾನ್ಯವಾಗಿ ಈ ರೀತಿಯ ವಿಶೇಷ ಪ್ರವಾಹವನ್ನು “ಸಮಾನ ಪ್ರವಾಹ” ಎಂದು ಕರೆಯುತ್ತೇವೆ. ಇಲ್ಲಿ ಸಮಾನ ಎಂದರೆ ಅದು ಸಾಮಾನ್ಯ ವಹನ ಪ್ರವಾಹದ ಆಧಾರದ ಮೇಲೆ ಕಾಂತಕ್ಷೇತ್ರವನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ!

ಜ್ಞಾಪನೆ: ಸರ್ಕ್ಯೂಟ್ ವಿಶ್ಲೇಷಣೆಯಲ್ಲಿ “ಸಮಾನ ಸರ್ಕ್ಯೂಟ್” ನೊಂದಿಗೆ ಇಲ್ಲಿ “ಸಮಾನ ಪ್ರವಾಹ” ವನ್ನು ಗೊಂದಲಗೊಳಿಸಬೇಡಿ

ವಾಸ್ತವವಾಗಿ, ನಾವು ಮೊದಲು ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಅಧ್ಯಯನ ಮಾಡಿದಾಗ, ಬಯೋಟ್-ಸಫರ್ ನಿಯಮದಲ್ಲಿನ ವಿದ್ಯುತ್ ಪ್ರವಾಹವು ಈ ಸಮಾನವಾದ ಪ್ರವಾಹವನ್ನು ಒಳಗೊಂಡಿರುವ ಸಾಮಾನ್ಯ ವಿದ್ಯುತ್ ಪ್ರವಾಹವಾಗಿದೆ. ಸಹಜವಾಗಿ, ಮ್ಯಾಕ್ಸ್ವೆಲ್ನ ಸಮೀಕರಣಗಳಲ್ಲಿನ ವಹನ ಪ್ರವಾಹವು ಸಾಮಾನ್ಯೀಕರಿಸಿದ ಪ್ರವಾಹವನ್ನು ಸಹ ಸೂಚಿಸುತ್ತದೆ.

ದ್ಯುತಿವಿದ್ಯುತ್ ಪರಿಣಾಮವನ್ನು ಅಧ್ಯಯನ ಮಾಡಿದವರಿಗೆ ದ್ಯುತಿವಿದ್ಯುಜ್ಜನಕವು ಕ್ಯಾಥೋಡ್‌ನಿಂದ ಆನೋಡ್‌ಗೆ ಚಲಿಸಿದಾಗ, ಗಾಳಿಯ ಪ್ರಭಾವವನ್ನು ನಿರ್ಲಕ್ಷಿಸಿದರೆ, ಈ ಪ್ರವಾಹವು ನಿರ್ವಾತದಲ್ಲಿನ ವಿದ್ಯುದಾವೇಶಗಳ ಚಲನೆಯಿಂದ ಉಂಟಾಗುತ್ತದೆ ಮತ್ತು ಯಾವುದೇ ಪ್ರತಿರೋಧವಿಲ್ಲ, ಆದ್ದರಿಂದ ಅದು ಓಮ್ನ ಕಾನೂನಿನಿಂದ ನಿರ್ಬಂಧಿಸಲಾಗಿಲ್ಲ.

ಹಾಗಾದರೆ, ಭೌತಶಾಸ್ತ್ರದಲ್ಲಿ ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಬಗ್ಗೆ ಇದು ಒಂದೇ ವಿಷಯವೇ?

ಇಲ್ಲ! ಎರಡು ವಿಧಗಳಿವೆ, ಅವುಗಳೆಂದರೆ ಮ್ಯಾಗ್ನೆಟೈಸಿಂಗ್ ಕರೆಂಟ್ ಮತ್ತು ಡಿಸ್ಪ್ಲೇಸ್ಮೆಂಟ್ ಕರೆಂಟ್.

ಅವು ಎರಡು ಸಮಾನ ಪ್ರವಾಹಗಳಾಗಿವೆ, ಹೆಸರೇ ಸೂಚಿಸುವಂತೆ, ಕಾಂತೀಯತೆಯನ್ನು ವಿವರಿಸಲು ಸಹ ಪರಿಚಯಿಸಲಾಗಿದೆ. ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಅವರು ಪ್ರಸ್ತುತ “ಚಾರ್ಜ್ ಚಳುವಳಿ” ಯ ಮೂಲಭೂತ ಗುಣಲಕ್ಷಣದಿಂದ ದೂರ ಹೋಗಿದ್ದಾರೆ!

ಆಶ್ಚರ್ಯಕರ! ವಿದ್ಯುದಾವೇಶದ ಚಲನೆ ಇಲ್ಲ, ಆದ್ದರಿಂದ ಅದನ್ನು ವಿದ್ಯುತ್ ಪ್ರವಾಹ ಎಂದು ಏಕೆ ಕರೆಯಬಹುದು?

ಚಿಂತಿಸಬೇಡಿ ಮತ್ತು ನನ್ನ ಮಾತನ್ನು ನಿಧಾನವಾಗಿ ಆಲಿಸಿ.

ಮೊದಲು ಮ್ಯಾಗ್ನೆಟೈಸಿಂಗ್ ಕರೆಂಟ್ ಅನ್ನು ನೋಡೋಣ.

ಕಾಂತೀಯತೆಯು ವಿದ್ಯುತ್ ಚಲನೆಯಿಂದ ಉಂಟಾಗುತ್ತದೆ ಎಂದು ಕಂಡುಬಂದಿದೆ (ಸದ್ಯಕ್ಕೆ ಸ್ಪಿನ್‌ನ ಆಂತರಿಕ ಗುಣಲಕ್ಷಣಗಳಿಂದ ಕಾಂತೀಯತೆಯ ವಿವರಣೆಯನ್ನು ಪರಿಗಣಿಸುವುದಿಲ್ಲ). ನೈಸರ್ಗಿಕ ಕಾಂತೀಯತೆಯನ್ನು ವಿವರಿಸುವ ಸಲುವಾಗಿ, ಫ್ರೆಂಚ್ ಭೌತಶಾಸ್ತ್ರಜ್ಞ ಆಂಪಿಯರ್ “ಆಣ್ವಿಕ ಪರಿಚಲನೆ” ಯ ಊಹೆಯನ್ನು ಮುಂದಿಟ್ಟರು.

ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ, ಯಾವುದೇ ಪರಮಾಣು ಅಥವಾ ಅಣುವನ್ನು ಕೇಂದ್ರದ ಸುತ್ತಲೂ ವಿದ್ಯುತ್ ಚಾರ್ಜ್ ಹೊಂದಿರುವಂತೆ ಪರಿಗಣಿಸಬಹುದು, ಇದು ಒಂದು ಸಣ್ಣ ಲೂಪ್ ಪ್ರವಾಹವನ್ನು ರೂಪಿಸುತ್ತದೆ, ಅಂದರೆ, “ಆಣ್ವಿಕ ಪರಿಚಲನೆ”.

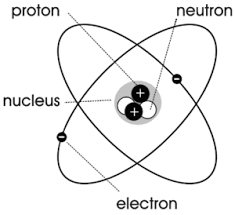
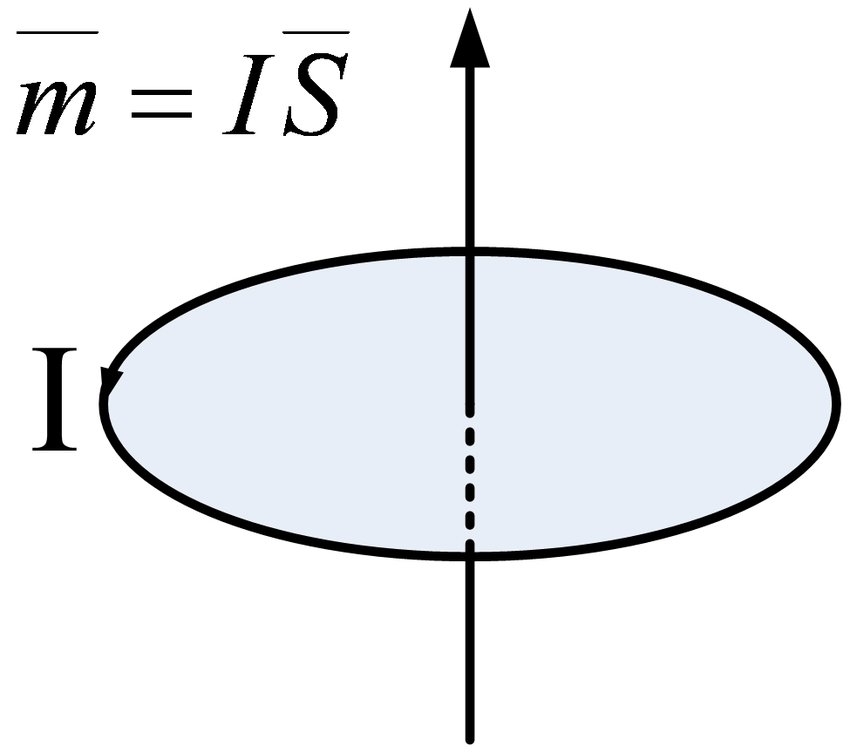
ವಿದ್ಯುತ್ ಪ್ರವಾಹವು ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಪ್ರಚೋದಿಸುತ್ತದೆ ಎಂಬ ಕಾನೂನಿನ ಪ್ರಕಾರ, ಈ ಆಣ್ವಿಕ ಪರಿಚಲನೆಯು ಕಾಂತೀಯ ಕ್ಷಣ ಎಂಬ ಭೌತಿಕ ಪ್ರಮಾಣವನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ. ಇದರ ಗಾತ್ರವು ಆಣ್ವಿಕ ಪರಿಚಲನೆಯಿಂದ ಸುತ್ತುವರಿದ ಪ್ರದೇಶವಾಗಿದ್ದು, ಆಣ್ವಿಕ ಪರಿಚಲನೆಯ ಸಮಾನ ಪ್ರವಾಹದಿಂದ ಗುಣಿಸಲ್ಪಡುತ್ತದೆ ಮತ್ತು ಅದರ ದಿಕ್ಕು ಪರಿಚಲನೆಯ ದಿಕ್ಕಿನೊಂದಿಗೆ ಬಲಗೈ ಸುರುಳಿಯ ಸಂಬಂಧದಲ್ಲಿದೆ, ಅವುಗಳೆಂದರೆ

ನಿಸ್ಸಂಶಯವಾಗಿ, ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷಣದ ದಿಕ್ಕು ನಿಖರವಾಗಿ ಪರಿಚಲನೆಯ ಪ್ರವಾಹದಿಂದ ರೂಪುಗೊಂಡ ಕಾಂತಕ್ಷೇತ್ರದ ದಿಕ್ಕಿನಲ್ಲಿದೆ.

.

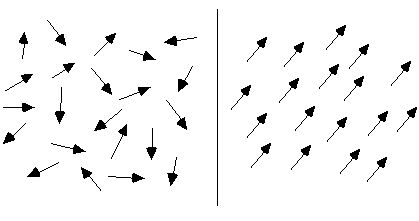
ಸಾಮಾನ್ಯ ಸಂದರ್ಭಗಳಲ್ಲಿ, ವಸ್ತುವಿನ ಆಣ್ವಿಕ ಪರಿಚಲನೆಯ ವ್ಯವಸ್ಥೆಯು ಅಸ್ತವ್ಯಸ್ತವಾಗಿದೆ, ಆದ್ದರಿಂದ ಕೆಳಗಿನ ಚಿತ್ರದ ಎಡಭಾಗದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ವಸ್ತುವು ಕಾಂತೀಯವಾಗಿರುವುದಿಲ್ಲ. ಬಾಹ್ಯ ಕಾಂತೀಯ ಕ್ಷೇತ್ರಕ್ಕೆ ಒಳಪಡಿಸಿದಾಗ, ಈ ಆಣ್ವಿಕ ಪರಿಚಲನೆಗಳು ಸರಿಸುಮಾರು ಅಂದವಾಗಿ ಜೋಡಿಸಲ್ಪಡುತ್ತವೆ. ಕೆಳಗಿನ ಆಕೃತಿಯ ಬಲಭಾಗದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ, ಅಸಂಖ್ಯಾತ ಸಣ್ಣ ಕಾಂತೀಯ ಸೂಜಿಗಳು ಒಟ್ಟುಗೂಡಿ ಒಟ್ಟು ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ರೂಪಿಸುವಂತೆ, ಅವುಗಳ ಕಾಂತೀಯ ಕ್ಷಣಗಳನ್ನು ಸಾಧ್ಯವಾದಷ್ಟು ಒಂದು ದಿಕ್ಕಿನಲ್ಲಿ ಜೋಡಿಸಲಾಗಿದೆ ಮತ್ತು ಅವುಗಳಿಂದ ಕೂಡಿದ ಸಂಪೂರ್ಣ ವಸ್ತುವು ಕಾಂತೀಯವಾಗುತ್ತದೆ.

ಒಂದು ಸಿಲಿಂಡರಾಕಾರದ ಮ್ಯಾಗ್ನೆಟ್ ಇದೆ ಎಂದು ಭಾವಿಸೋಣ, ಒಳಗಿನ ಆಣ್ವಿಕ ಪರಿಚಲನೆಯು ಅಂದವಾಗಿ ಜೋಡಿಸಲ್ಪಟ್ಟಿರುತ್ತದೆ ಮತ್ತು ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ಮ್ಯಾಗ್ನೆಟ್ ವಿಭಾಗದ ಅಂಚಿನಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು ಆಣ್ವಿಕ ಪರಿಚಲನೆಯ ವಿಭಾಗಗಳು ಒಂದು ದೊಡ್ಡ ಪರಿಚಲನೆಯನ್ನು ರೂಪಿಸಲು ಒಟ್ಟಿಗೆ ಜೋಡಿಸಲ್ಪಟ್ಟಿವೆ.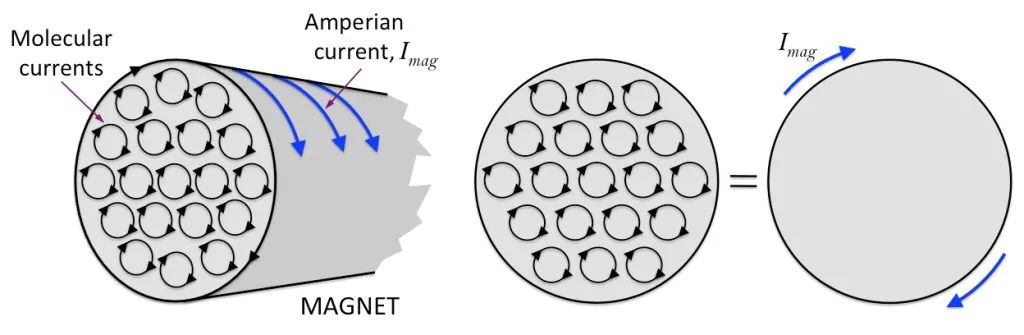

ಇದರ ಆಧಾರದ ಮೇಲೆ, ಬಾರ್ ಮ್ಯಾಗ್ನೆಟ್ ಶಕ್ತಿಯುತವಾದ ಸೊಲೀನಾಯ್ಡ್‌ನಂತೆ ಎಂದು ನಾವು ಭಾವಿಸಬಹುದು. ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಅಯಸ್ಕಾಂತದ ಮೇಲ್ಮೈಯಲ್ಲಿ ಸಿಕ್ಕಿಹಾಕಿಕೊಂಡಿರುವ ಅಗೋಚರ ಪ್ರವಾಹವಿದೆ! ಈ ರೀತಿಯ ಕರೆಂಟ್ ಅನ್ನು ಸಂಪರ್ಕಿಸಲು ಮತ್ತು ಬಳಸಲಾಗುವುದಿಲ್ಲ. ಇದು ಆಯಸ್ಕಾಂತದ ಮೇಲ್ಮೈಗೆ ಸೀಮಿತವಾಗಿದೆ. ನಾವು ಅದನ್ನು “ಬೈಂಡಿಂಗ್ ಕರೆಂಟ್” ಅಥವಾ “ಮ್ಯಾಗ್ನೆಟೈಸಿಂಗ್ ಕರೆಂಟ್” ಎಂದು ಕರೆಯುತ್ತೇವೆ.

ಆದ್ದರಿಂದ, ಮ್ಯಾಗ್ನೆಟೈಸಿಂಗ್ ಪ್ರವಾಹವು ಪ್ರಸ್ತುತವಾಗಿದೆ, ಏಕೆಂದರೆ ಇದು ನೈಜ ವಿದ್ಯುದಾವೇಶಗಳ ಚಲನೆಯಿಂದ ರೂಪುಗೊಂಡ ಪ್ರವಾಹದಂತೆಯೇ ಇರುತ್ತದೆ, ಇದು ಸಮಾನವಾಗಿ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ!

ಸ್ಥಳಾಂತರದ ಪ್ರವಾಹವನ್ನು ಮತ್ತೊಮ್ಮೆ ನೋಡೋಣ.

ಆಂಪಿಯರ್‌ನ ಲೂಪ್ ಪ್ರಮೇಯದ ಪ್ರಕಾರ, ಮುಚ್ಚಿದ ಹಾದಿಯಲ್ಲಿನ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯ ಅವಿಭಾಜ್ಯವು ಈ ಮಾರ್ಗದಿಂದ ಸುತ್ತುವರಿದ ಯಾವುದೇ ಬಾಗಿದ ಮೇಲ್ಮೈಯಲ್ಲಿ ಪ್ರಸ್ತುತ ಸಾಂದ್ರತೆಯ ಫ್ಲಕ್ಸ್‌ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ, ಈ ಪ್ರಮೇಯವನ್ನು ಗಣಿತಶಾಸ್ತ್ರದಲ್ಲಿ ಸ್ಟೋಕ್ಸ್ ಪ್ರಮೇಯ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಯಾವುದೇ ಮುಚ್ಚಿದ ಹಾದಿಯಲ್ಲಿ ವೆಕ್ಟರ್‌ನ ಅವಿಭಾಜ್ಯವು ಮುಚ್ಚಿದ ಮಾರ್ಗದಿಂದ ಸುತ್ತುವರೆದಿರುವ ಯಾವುದೇ ಮೇಲ್ಮೈಗೆ ಅದರ ಸುರುಳಿಯ (ಇಲ್ಲಿ) ಫ್ಲಕ್ಸ್‌ಗೆ ಸಮನಾಗಿರಬೇಕು ಎಂದು ಅದು ನಮಗೆ ಹೇಳುತ್ತದೆ.

ಇದು ಗಣಿತದ ಪ್ರಮೇಯವಾಗಿರುವುದರಿಂದ, ಇದು ಯಾವಾಗಲೂ ಸರಿಯಾಗಿರಬೇಕು, ಏಕೆಂದರೆ ಗಣಿತವು ಮೂಲತತ್ವಗಳ ಆಧಾರದ ಮೇಲೆ ತಾರ್ಕಿಕ ವ್ಯವಸ್ಥೆಯಾಗಿದೆ.

ಆದ್ದರಿಂದ, ಆಂಪಿಯರ್ ಲೂಪ್ ಪ್ರಮೇಯವು ಯಾವಾಗಲೂ ಹಿಡಿದಿರಬೇಕು!

ಆದಾಗ್ಯೂ, ಪ್ರತಿಭಾವಂತ ಸ್ಕಾಟಿಷ್ ಭೌತಶಾಸ್ತ್ರಜ್ಞ ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ಅಸ್ಥಿರ ಪ್ರಸ್ತುತ ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ಎದುರಿಸಿದಾಗ, ಆಂಪಿಯರ್ ಲೂಪ್ ಪ್ರಮೇಯವು ವಿರೋಧಾತ್ಮಕವಾಗಿದೆ ಎಂದು ಕಂಡುಹಿಡಿದನು.

ಕೆಪಾಸಿಟರ್ನ ಚಾರ್ಜಿಂಗ್ ಮತ್ತು ಡಿಸ್ಚಾರ್ಜ್ ಸಮಯದಲ್ಲಿ ವಿಶಿಷ್ಟವಾದ ಅಸ್ಥಿರ ಪ್ರವಾಹವು ಸಂಭವಿಸುತ್ತದೆ. ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ, ಕೆಪಾಸಿಟರ್ ಚಾರ್ಜಿಂಗ್ನ ಅಲ್ಪಾವಧಿಯಲ್ಲಿ ಅಸ್ಥಿರ ಪ್ರವಾಹವಿದೆ.

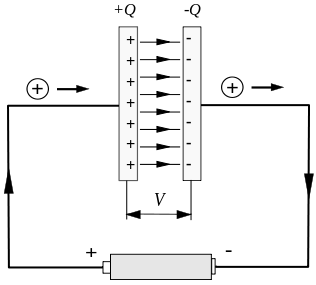
ಆದರೆ ಕೆಪಾಸಿಟರ್ ಪ್ಲೇಟ್‌ಗಳ ನಡುವೆ ಸರ್ಕ್ಯೂಟ್ ಸಂಪರ್ಕ ಕಡಿತಗೊಂಡಿದೆ, ಇದು ಗಂಭೀರ ಸಮಸ್ಯೆಯನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ.

ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ತಂತಿಯನ್ನು ಬೈಪಾಸ್ ಮಾಡುವ ಮುಚ್ಚಿದ ಮಾರ್ಗವನ್ನು ನಾವು ಪರಿಗಣಿಸುತ್ತೇವೆ ಎಂದು ಭಾವಿಸೋಣ, C ನಿಂದ ಗುರುತಿಸಲಾದ ವೃತ್ತ ಮತ್ತು ಅದರೊಂದಿಗೆ ಬಾಗಿದ ಮೇಲ್ಮೈಯನ್ನು ಅನಿಯಂತ್ರಿತವಾಗಿ ಆಯ್ಕೆ ಮಾಡಬಹುದು. ಚಿತ್ರದಲ್ಲಿ, ಸಿ ಸ್ವತಃ ಮತ್ತು ಕೆಪಾಸಿಟರ್ ಅಡ್ಡಲಾಗಿ ಸುತ್ತುವರಿದ ವೃತ್ತಾಕಾರದ ಸಮತಲವನ್ನು ಆಯ್ಕೆಮಾಡಲಾಗಿದೆ. ಎಡ ಫಲಕದ ಬಾಗಿದ ಮೇಲ್ಮೈ.

ವೃತ್ತಾಕಾರದ ಮೇಲ್ಮೈ ಪ್ರಕಾರ, ಬಾಗಿದ ಮೇಲ್ಮೈ ಪ್ರಕಾರ, ಆದರೆ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯ ಲೂಪ್ ಅವಿಭಾಜ್ಯವಾಗಿ, ಅದರ ಮೌಲ್ಯವನ್ನು ನಿರ್ಧರಿಸಬೇಕು ಎಂದು ನೋಡಬಹುದು!

ಹೇಗೆ ಮಾಡುವುದು?

ಆಂಪಿಯರ್‌ನ ಲೂಪ್ ಪ್ರಮೇಯವನ್ನು ಸ್ಥಾಪಿಸಬೇಕು ಎಂದು ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ನಂಬುತ್ತಾರೆ. ಈಗ ಒಂದು ಸಮಸ್ಯೆ ಇದೆ, ಅದು ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಒಂದು ಭಾಗವನ್ನು ನಾವು ಮೊದಲು ಕಂಡುಹಿಡಿಯದ ಕಾರಣ ಇರಬೇಕು, ಆದರೆ ಅದು ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ!

ಆದ್ದರಿಂದ, ಪ್ರಸ್ತುತದ ಈ ಭಾಗವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಹೇಗೆ?

ಪ್ಲೇಟ್‌ಗಳ ನಡುವೆ ಸಮಸ್ಯೆ ಇರುವುದರಿಂದ, ಪ್ಲೇಟ್‌ಗಳ ನಡುವೆ ಪ್ರಾರಂಭಿಸಿ.

ವಿಶ್ಲೇಷಣೆಯ ಮೂಲಕ, ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ಚಾರ್ಜಿಂಗ್ ಅಥವಾ ಡಿಸ್ಚಾರ್ಜ್ ಮಾಡುವುದನ್ನು ಲೆಕ್ಕಿಸದೆ, ಎಲ್ಲಾ ಸಮಯದಲ್ಲೂ ಕೆಪಾಸಿಟರ್ ಪ್ಲೇಟ್‌ಗಳ ನಡುವೆ ಭೌತಿಕ ಪ್ರಮಾಣವಿದೆ, ಅದು ಪ್ರಸ್ತುತದ ಪ್ರಮಾಣ ಮತ್ತು ದಿಕ್ಕಿನೊಂದಿಗೆ ಸಿಂಕ್ರೊನೈಸ್ ಆಗುತ್ತದೆ. ಇದು ಎಲೆಕ್ಟ್ರಿಕ್ ಡಿಸ್ಪ್ಲೇಸ್ಮೆಂಟ್ ವೆಕ್ಟರ್ನ ಫ್ಲಕ್ಸ್ನ ಸಮಯದ ಉತ್ಪನ್ನವಾಗಿದೆ, ಅಂದರೆ, ಇದನ್ನು ಡಿಸ್ಪ್ಲೇಸ್ಮೆಂಟ್ ಕರೆಂಟ್ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ.

ಈ ಭಾಗವು ಮೊದಲು ಕಂಡುಹಿಡಿಯದ ಪ್ರವಾಹದ ಭಾಗವಾಗಿದೆ ಎಂದು ಪರಿಗಣಿಸಿದರೆ, ನಂತರ ಸಂಪೂರ್ಣ ಕರೆಂಟ್ ಈಗ. ಅಂದರೆ, ಪ್ಲೇಟ್‌ಗಳ ನಡುವಿನ ಸರ್ಕ್ಯೂಟ್ ಸಂಪರ್ಕ ಕಡಿತಗೊಂಡಿದ್ದರೂ, ಎಲೆಕ್ಟ್ರಿಕ್ ಡಿಸ್ಪ್ಲೇಸ್‌ಮೆಂಟ್ ಫ್ಲಕ್ಸ್‌ನ ವ್ಯುತ್ಪನ್ನ ಮತ್ತು ಪ್ರವಾಹದ ಮೊತ್ತವು ಒಟ್ಟಾರೆಯಾಗಿ , ಎಲ್ಲಾ ಸಮಯದಲ್ಲೂ ಪ್ರಸ್ತುತದ ನಿರಂತರತೆಯನ್ನು ಖಚಿತಪಡಿಸಿಕೊಳ್ಳಿ.

ಹಿಂದಿನ ವಿರೋಧಾಭಾಸಕ್ಕೆ ಹಿಂತಿರುಗಿ, ಸ್ಟೋಕ್ಸ್ ಪ್ರಮೇಯದ ಅವಶ್ಯಕತೆಗಳ ಪ್ರಕಾರ, ಮುಚ್ಚಿದ ಮೇಲ್ಮೈಗೆ ಪ್ರಸ್ತುತ ಸಾಂದ್ರತೆಯ ಹರಿವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವಾಗ, ಸ್ಥಳಾಂತರದ ಪ್ರವಾಹದ ಸಾಂದ್ರತೆಯನ್ನು ಸಹ ಪರಿಗಣಿಸಬೇಕು, ಅಂದರೆ ಸಂಪೂರ್ಣ ಆಂಪಿಯರ್ ಲೂಪ್ ಎಂದು ನಮಗೆ ತಿಳಿದಿದೆ. ಪ್ರಮೇಯವು ಆದ್ದರಿಂದ, ಈ ಹೊಸ ಪ್ರಸ್ತುತ ಘಟಕವನ್ನು “ಶೋಧಿಸುವ” ಮೂಲಕ, ಆಂಪಿಯರ್ ಲೂಪ್ ಪ್ರಮೇಯದ ಬಿಕ್ಕಟ್ಟನ್ನು ಪರಿಹರಿಸಲಾಗಿದೆ!

ಇಲ್ಲಿ “ಪರಿಚಯ” ಬಳಸದಿರುವ ಕಾರಣ, ಆದರೆ “ಆವಿಷ್ಕಾರ” ಅನ್ನು ಇಲ್ಲಿ ಬಳಸಲಾಗಿದೆ. ಈ ರೀತಿಯ ಪ್ರವಾಹವು ಗಣಿತದ ಪರಿಹಾರವಲ್ಲ, ಆದರೆ ನಿಜವಾದ ವಿಷಯ ಎಂದು ನಾನು ಒತ್ತಿಹೇಳಲು ಬಯಸುತ್ತೇನೆ, ಆದರೆ ಅದನ್ನು ಮೊದಲು ಕಂಡುಹಿಡಿಯಲಾಗಿಲ್ಲ.

ಇದು ಮೊದಲ ಸ್ಥಾನದಲ್ಲಿ ಏಕೆ ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ? ಇದು ವಿದ್ಯುತ್ ಪ್ರವಾಹದಂತೆ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಕಾರಣ, ವಹನ ಪ್ರವಾಹದಂತೆ, ಇದು ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಸಮಾನವಾಗಿ ಪ್ರಚೋದಿಸುತ್ತದೆ, ವಿದ್ಯುತ್ ಶುಲ್ಕಗಳ ಚಲನೆ ಇಲ್ಲ, ಯಾವುದೇ ತಂತಿ ಅಗತ್ಯವಿಲ್ಲ ಮತ್ತು ಜೌಲ್ ಶಾಖವನ್ನು ಉತ್ಪಾದಿಸಲಾಗುವುದಿಲ್ಲ, ಆದ್ದರಿಂದ ಅದನ್ನು ನಿರ್ಲಕ್ಷಿಸಲಾಗಿದೆ!

ಆದರೆ ಅದು ನಿಜವಾಗಿಯೂ ಸ್ವತಃ ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ, ಕಡಿಮೆ ಪ್ರೊಫೈಲ್ ಅನ್ನು ಇರಿಸಿಕೊಳ್ಳಿ, ಅದು ಎಲ್ಲಾ ಸಮಯದಲ್ಲೂ ಕಾಂತಕ್ಷೇತ್ರವನ್ನು ಮೌನವಾಗಿ ರೋಮಾಂಚನಗೊಳಿಸುತ್ತಿದೆ!

ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ನಾವು ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಎದುರಿಸಿದಾಗ, ಪ್ರಸ್ತುತದ ಮೂಲ ವ್ಯಾಖ್ಯಾನವು ತುಂಬಾ ಕಿರಿದಾಗಿರುತ್ತದೆ. ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಮೂಲತತ್ವವು ವಿದ್ಯುದಾವೇಶದ ಚಲನೆಯಲ್ಲ, ಅದು ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಪ್ರಚೋದಿಸುವಂತಿರಬೇಕು.

ಇಲ್ಲಿಯವರೆಗೆ, ಪ್ರಸ್ತುತದ ಹಲವಾರು ರೂಪಗಳನ್ನು ಪರಿಚಯಿಸಲಾಗಿದೆ. ಅವೆಲ್ಲವೂ ವಸ್ತುನಿಷ್ಠವಾಗಿ ಅಸ್ತಿತ್ವದಲ್ಲಿವೆ, ಮತ್ತು ಅವುಗಳು ಸಾಮಾನ್ಯವಾಗಿದ್ದು, ಎಲ್ಲಾ ಪ್ರವಾಹಗಳು ಸಮಾನವಾಗಿ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಪ್ರಚೋದಿಸಬಹುದು.