Mikä on sähkövirta? Muista ensin, mikä on virran määritelmä, jonka olemme oppineet?

Yksinkertaisesti sanottuna varautuneiden hiukkasten suuntainen liike johtimessa on sähkövirtaa.

Vain kun aineessa on varautuneita hiukkasia, jotka voivat liikkua vapaasti, se voi siirtää sähkövirtaa eli johtaa sähköä. Näitä varautuneita hiukkasia, jotka osallistuvat johtamiseen, kutsutaan kantajiksi. Esimerkiksi metalleille vain atomien ulommat elektronit voivat toimia kantajina.

“Suunnattu liike” sähkövirran määritelmässä ymmärretään usein väärin. Monien mielestä se viittaa liikettä tiettyyn suuntaan, ei tietenkään! Eikö elektronien liikesuunta vaihtovirtapiirissä muutu?

Itse asiassa suunnistus on suhteessa “satunnaiseen liikkeeseen”!

Koska elektronit ovat mikroskooppisia hiukkasia, niiden on oltava lämpöliikkeessä koko ajan. Lämpöliike on satunnaista liikettä, kuten alla olevasta kuvasta näkyy.

Tämä liike on itse asiassa erittäin nopea. Esimerkiksi metalleissa huoneenlämmössä elektronisen lämpöliikkeen nopeus on luokkaa satoja kilometrejä sekunnissa!

Jos katsot tarkkaan tätä satunnaista liikettä, huomaat, että jokaisen hiukkasen liikesuunta on satunnainen milloin tahansa. Jos lasket yhteen näiden hiukkasten nopeusvektorit, tulos on melkein nolla.

Lisää nyt johtimeen sähkökenttä, jolloin elektroni suorittaa suunnatun liikkeen satunnaisen liikkeen perusteella. Olettaen, että sähkökenttä on vasemmalla tietyn ajan, elektronien liike näyttää seuraavalta. Punaiset pallot edustavat metalliatomeja kidehilassa ja nopeasti liikkuvat pisteet edustavat vapaita elektroneja.

Näyttääkö se nopealta? Tämä johtuu siitä, että elektroninen liike on todella nopeaa! Mutta itse asiassa satunnainen liike, joka muodostaa suuren osan siitä, ei vaikuta virtaan. Kun satunnainen liike on eliminoitu, loppu on aivan kuten alla oleva hidas katse.

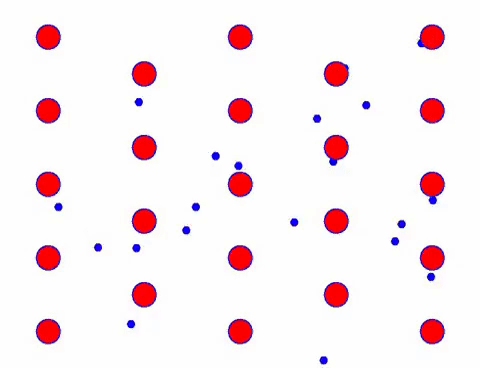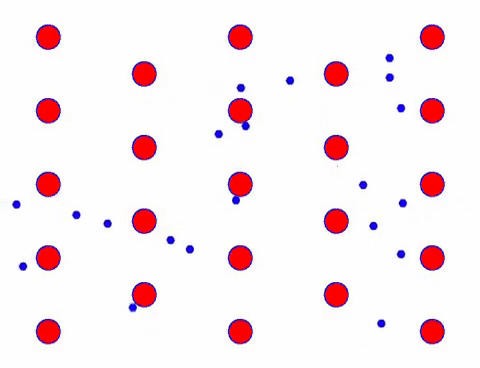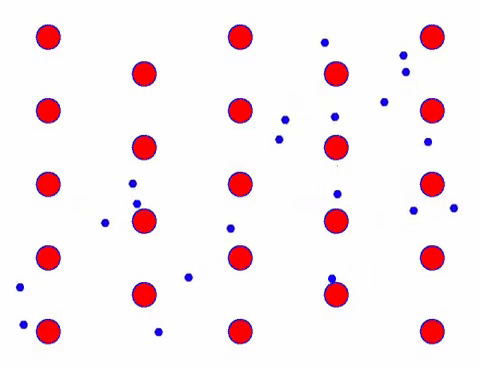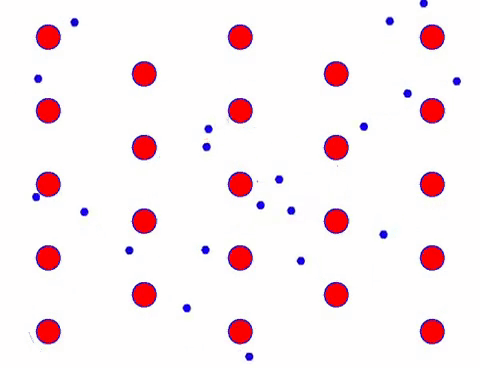
Itse asiassa elektronien suunnattu liike on paljon hitaampaa kuin lämpöliikkeen nopeus. Tätä elektronien “hiontaista” liikettä kutsutaan driftiksi tai “driftiksi”. Joskus elektronit juoksevat vastakkaiseen suuntaan törmäysten vuoksi atomien kanssa. Mutta yleensä elektronit liikkuvat yhteen suuntaan.

If the electric field changes direction, the direction of electron drift will also change.

Therefore, this kind of directional movement means that the sum of the speeds of all the electrons participating in the conduction at a certain time is not zero, but is generally in a certain direction. This direction can be changed at any time, and that is the case of alternating current.

Siksi virta ei ole niinkään sähkövarauksen “suunnattua liikettä”, vaan se on sähkövarauksen “kollektiivinen liike”.

Johtimen virran suuruus ilmaistaan ​​virran intensiteetillä. Virran intensiteetti määritellään sähkömääräksi, joka kulkee johtimen poikkileikkauksen läpi yksikköajassa, ts.

We have learned some physical quantities that contain the word “intensity”, such as electric field intensity and magnetic induction intensity. They generally represent the apportionment per unit time, unit area (or unit volume, unit solid angle). However, the word “intensity” in the current intensity does not reflect the current apportionment of the area.

Itse asiassa toinen fyysinen suure on vastuussa virran jakautumisesta alueelle, joka on virrantiheys.

Koska sähkövirran olemus on sähkövarauksen suuntainen liike, virran voimakkuuden ja ryömintänopeuden välillä on oltava tietty suhde!

Tämän suhteen saamiseksi on ensin selvitettävä käsite-kantaja-ainepitoisuus, eli kantaja-aineiden lukumäärä tilavuusyksikköön, joka ilmaistaan ​​:llä.

Oletetaan, että johtimen poikkileikkaus on, kantoaaltopitoisuus on, ryömintänopeus on ja varautunut varaus on.

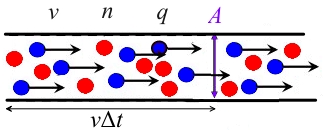
Tällöin pinnan vasemmalla puolella olevan johtimen varaus on, ja nämä varaukset kulkevat pinnan läpi tietyn ajan sisällä, joten

This is a microscopic expression of current intensity.

Virtatiheys on virran jakautuminen pinta-alaan, joten virrantiheyden suuruus on, mutta se määritellään vektoriksi ja suunta on positiivisesti varautuneiden kantajien ryömintänopeusvektorin suunta, joten elektronien ajautuminen metallia voidaan saada tästä Speedistä alla olevan esimerkin mukaisesti.

Consider a copper wire, assuming that each copper atom contributes an electron as a carrier. There is 1 mol of copper, its volume is, molar mass is, density is, then the carrier concentration of the copper wire is

Missä on Avogadron vakio. Kuparin tiheys löytyy ja korvaamalla saatu arvo on noin yksikkö/kuutiometri.

Olettaen, että kuparilangan säde on 0.8 mm, virtaava virta on 15A, =1.6 C ja elektronien ryömintänopeus lasketaan

Voidaan nähdä, että elektronien ryömintänopeus on todella pieni.

Niille, jotka opiskelevat piirejä, yllä oleva on täydellinen virran määritelmä.

But in physics, the above definition of current is actually only a narrow definition. More general currents are not limited to conductors, as long as the movement of electric charges is current. For example, when the electrons of a hydrogen atom move around the nucleus, an electric current is formed in its orbit.

Oletetaan, että elektronisen latauksen määrä on ja liikejakso on. Sitten joka kerta kun se kuluu, niin suuri määrä varausta kulkee minkä tahansa silmukan poikkileikkauksen läpi, joten virran intensiteetti perustuu jakson, taajuuden ja kulmanopeuden väliseen suhteeseen, ja virta voidaan myös ilmaista

Toisessa esimerkissä varautunut metallilevy, joka pyörii akselinsa ympäri, muodostaa myös erisäteisiä silmukkavirtoja.

Tällainen virta ei ole normaalia johtumisvirtaa, eikä se voi tuottaa Joule-lämpöä! Ei voi muodostaa todellista piiriä.

Otherwise, would you give me a calculation of how much joule heat is generated per second by the electrons of the hydrogen atom?

Itse asiassa tyhjiövirta ei täytä Ohmin lakia. Koska varautuneiden hiukkasten liikkeestä tyhjiössä muodostuvassa sähkövirrassa kantajat eivät törmää samalla tavalla kuin metallin hila, joten tyhjiöllä ei ole vastusta eikä johtavuutta.

Sähkövarausten liike synnyttää sähkövirtaa, ja sähkövaraus itse virittää sähkökentän. Tästä on helppo aiheuttaa väärinkäsitys. Monet ihmiset ajattelevat siksi, että sähkövirran muodostavien varautuneiden hiukkasten sähkökenttä on paljastettava. Mutta itse asiassa yleisjohtimessa olevalle johtavuusvirralle kantoaaltoja virtaa taustalla, joka koostuu suuresta määrästä positiivisesti varautuneita metalli-ioneja, ja itse johdin on neutraali!

Kutsumme usein tällaista erikoisvirtaa “ekvivalenttivirraksi”. Vastaava tässä tarkoittaa, että se synnyttää magneettikentän samalla perusteella kuin tavallinen johtumisvirta!

Reminder: Do not confuse the “equivalent current” here with the “equivalent circuit” in circuit analysis

Itse asiassa, kun tutkimme ensimmäisen kerran magneettikenttää, sähkövirta Biot-Saffarin laissa oli yleistetty sähkövirta, joka sisälsi tämän vastaavan virran. Tietenkin johtavuusvirta Maxwellin yhtälöissä viittaa myös yleistettyyn virtaan.

Valosähköistä vaikutusta tutkineet tietävät, että kun valoelektroni ajautuu katodilta anodille, jos ilman vaikutus jätetään huomiotta, tämä virta johtuu sähkövarausten liikkeestä tyhjiössä, eikä vastusta ole, joten se Ohmin laki ei rajoita sitä.

Onko tämä siis ainoa asia sähkövirrasta fysiikassa?

Ei! On myös kahta tyyppiä, nimittäin magnetointivirta ja siirtymävirta.

Ne ovat myös kaksi ekvivalenttia virtaa, jotka, kuten nimestä voi päätellä, otetaan käyttöön myös selittämään magnetismia. Toisin sanoen ne ovat irtautuneet nykyisen “latausliikkeen” perusominaisuudesta!

Se on hämmästyttävää! Sähkövarausliikettä ei ole, joten miksi sitä voidaan kutsua sähkövirraksi?

Älä huoli, vaan kuuntele minua hitaasti.

Katsotaan ensin magnetointivirtaa.

Todettiin, että magnetismi johtuu sähkön liikkeestä (ottamatta huomioon magnetismin selitystä spinin sisäisillä ominaisuuksilla toistaiseksi). Selittääkseen luonnollisen magnetismin ranskalainen fyysikko Ampere esitti hypoteesin “molekyylikierrosta”.

Kuten alla olevasta kuvasta näkyy, minkä tahansa atomin tai molekyylin voidaan katsoa sisältävän sähkövarauksen, joka pyörii keskustan ympärillä muodostaen pienen silmukkavirran eli “molekyylikierron”.

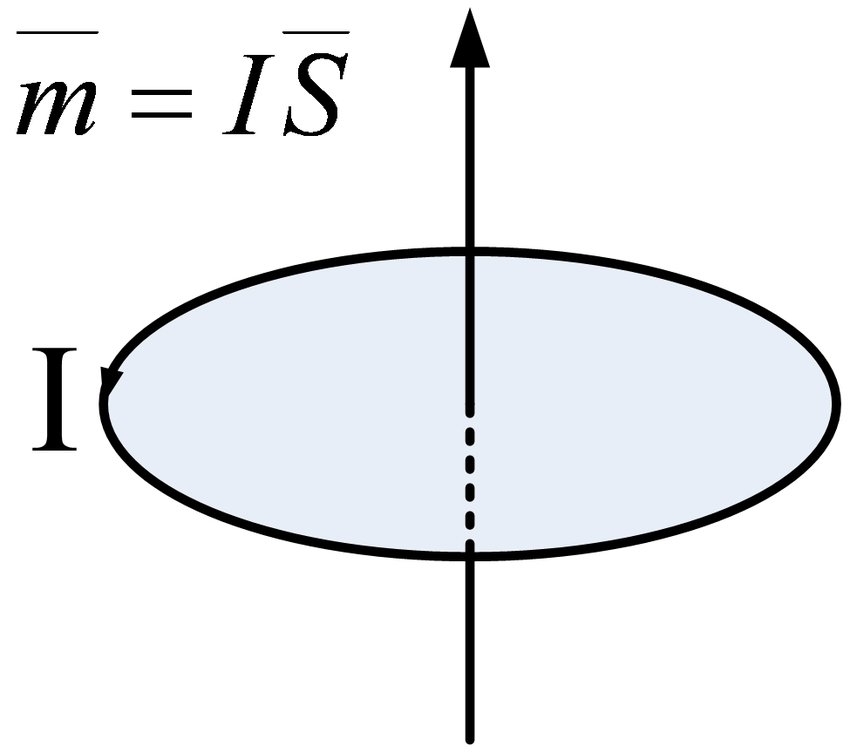
Sen lain mukaan, että sähkövirta virittää magneettikentän, tämä molekyylikierto tuottaa fyysisen suuren, jota kutsutaan magneettimomentiksi. Sen koko on molekyylikierron ympäröimä pinta-ala kerrottuna molekyylikierron ekvivalenttivirralla ja sen suunta on oikeakätisessä spiraalisuhteessa kierron suunnan kanssa, ts.

On selvää, että magneettisen momentin suunta on täsmälleen kiertovirran muodostaman magneettikentän suuntaa pitkin

.

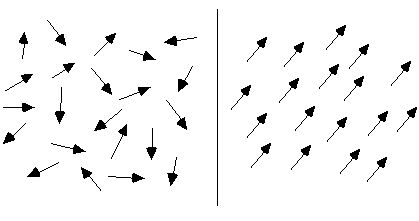
Normaalioloissa aineen molekyylikierron järjestely on kaoottinen, joten aine ei ole magneettinen, kuten alla olevan kuvan vasemmalla puolella näkyy. Kun ne altistetaan ulkoiselle magneettikentälle, nämä molekyylikierrot ovat suunnilleen siististi järjestettyjä. Kuten alla olevan kuvan oikealla puolella näkyy, niiden magneettiset momentit järjestetään mahdollisimman paljon yhteen suuntaan, aivan kuten lukemattomat pienet magneettiset neulat, jotka on koottu yhteen muodostamaan kokonaismagneettikentän, ja koko niistä muodostuva materiaali muuttuu magneettiseksi.

Oletetaan, että on sylinterimäinen magneetti, sisäinen molekyylikierto on siististi järjestetty ja kunkin molekyylikierron osat magneettiosan reunassa on yhdistetty toisiinsa suuren kierron muodostamiseksi, kuten alla olevassa kuvassa näkyy.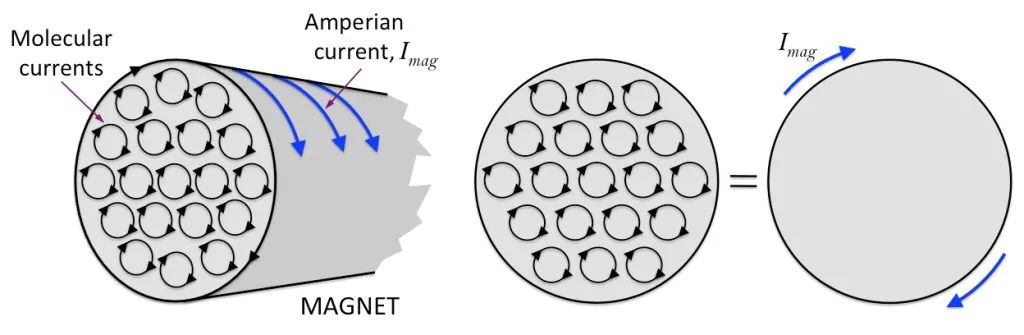

Tämän perusteella voimme ajatella, että tankomagneetti on kuin jännitteinen solenoidi. Toisin sanoen, magneetin pinnalle on sotkeutunut näkymätön virta! Tällaista virtaa ei voida kytkeä ja käyttää. Se rajoittuu magneetin pintaan. Kutsumme sitä “sidosvirraksi” tai “magnetoivaksi virraksi”.

Siksi magnetointivirta on virta, koska se on sama kuin todellisten sähkövarausten liikkeen muodostama virta, joka voi vastaavasti synnyttää magneettikentän!

Katsotaanpa syrjäytysvirtaa uudelleen.

Amperen silmukkalauseen mukaan magneettikentän voimakkuuden integraali suljetulla tiellä on yhtä suuri kuin virrantiheyden vuo millä tahansa tämän polun rajoittamalla kaarevalla pinnalla, eli tätä lausetta kutsutaan matematiikassa Stokesin lauseeksi. Se kertoo meille, että minkä tahansa suljetun polun varrella olevan vektorin integraalin on oltava yhtä suuri kuin sen kiertymisen vuo (tässä) mihin tahansa suljetun polun rajoittamaan pintaan.

Koska se on matemaattinen lause, sen on aina oltava oikein, koska matematiikka on aksioomeihin perustuva looginen järjestelmä.

Siksi ampeerisilmukkalauseen on aina oltava voimassa!

Lahjakas skotlantilainen fyysikko Maxwell kuitenkin huomasi, että kun kohtasi epävakaan virtapiirin, ampeerisilmukkalause oli ristiriitainen.

Tyypillinen epävakaa virta esiintyy kondensaattorin latauksen ja purkamisen aikana. Kuten alla olevasta kuvasta näkyy, virta on epävakaa kondensaattorin lyhyen latauksen aikana.

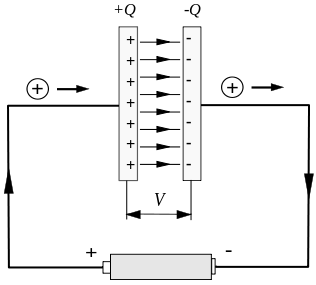
Mutta piiri on irrotettu kondensaattorilevyjen välillä, mikä aiheuttaa vakavan ongelman.

Oletetaan, että harkitaan suljettua polkua, joka ohittaa johdon, kuten alla olevassa kuvassa näkyy, C:llä merkitty ympyrä ja kaareva pinta, jonka rajana se on, voidaan valita mielivaltaisesti. Kuvassa on valittu C:n itsensä ympäröimä ja kondensaattorin poikki oleva pyöreä taso. Vasemman levyn kaareva pinta.

According to the circular surface, it can be seen that according to the curved surface, but as a loop integral of the magnetic field strength, its value should be determined!

Miten tehdä?

Maxwell uskoo, että Amperen silmukkalause on vahvistettava. Nyt kun on ongelma, sen täytyy johtua siitä, että emme ole aiemmin löytäneet osaa virrasta, mutta se on olemassa!

Joten kuinka selvittää tämä osa virtaa?

Koska ongelma on levyjen välissä, aloita levyjen välistä.

Analyysin avulla Maxwell havaitsi, että riippumatta latauksesta tai purkamisesta, kondensaattorilevyjen välillä on koko ajan fyysinen määrä, joka on synkronoitu virran suuruuden ja suunnan kanssa. Se on sähkösiirtymävektorin vuon aikaderivaata, eli se määritellään siirtymävirraksi.

If it is considered that this part is the part of the current that has not been discovered before, then the complete current is now. That is to say, although the circuit between the plates is disconnected, the derivative of the electric displacement flux and the sum of the current together, as a whole , Ensure the continuity of the current at all times.

Palataksemme edelliseen ristiriitaan, tiedämme nyt, että Stokesin lauseen vaatimusten mukaisesti suljetun pinnan virrantiheyden vuota laskettaessa tulee ottaa huomioon myös siirtymävirran tiheys, eli täydellinen ampeerisilmukka. lause on siis “Löytämällä” tämä uusi nykyinen komponentti, Ampere Loop -lauseen kriisi on ratkaistu!

Syy, miksi “johdanto” ei käytetä tässä, mutta “löytö” käytetään tässä. Haluan korostaa sitä, että tällainen virta ei ole matemaattinen kompensaatio, vaan todellinen asia, mutta sitä ei ole aiemmin löydetty.

Miksi se ylipäätään on olemassa? Koska se toimii sähkövirtana, kuten johtumisvirta, se virittää magneettikentän vastaavasti, paitsi että sähkövaraukset eivät liiku, johtoa ei tarvita eikä Joule-lämpöä voida tuottaa, joten se on jätetty huomiotta!

Mutta se on itse asiassa olemassa itsestään, pidä vain matalaa profiilia, se on hiljaa kiihottanut magneettikenttää siellä koko ajan!

Toisin sanoen, kun kohtaamme magneettikentän, alkuperäinen virran määritelmä on liian kapea. Sähkövirran ydin ei ole sähkövarauksen liike, vaan sen pitäisi olla jotain, joka voi herättää magneettikentän.

Tähän mennessä useita virtamuotoja on otettu käyttöön. Ne kaikki ovat olemassa objektiivisesti, ja niille on yhteistä se, että kaikki virrat voivat yhtä hyvin virittää magneettikenttää.