- 09
- Dec
Mi az Aktuális?
Mi az elektromos áram? Először is emlékezz, mi az áram definíciója, amelyet megtanultunk?

Egészen egyszerűen, a töltött részecskék irányított mozgása egy vezetőben elektromos áram.
Csak ha egy anyagban vannak töltött részecskék, amelyek szabadon mozoghatnak, akkor képes elektromos áramot továbbítani, azaz elektromos áramot vezetni. Ezeket a töltött részecskéket, amelyek részt vesznek a vezetésben, hordozóknak nevezzük. A fémeknél például csak az atomok külső elektronjai működhetnek hordozóként.
The “directional movement” in the definition of electric current is often misunderstood. Many people think it refers to movement with a certain direction, of course not! Doesn’t the direction of movement of the electrons in the AC circuit change?
In fact, orienteering is relative to “random movement”!
Mivel az elektronok mikroszkopikus részecskék, folyamatosan hőmozgásban kell lenniük. A hőmozgás véletlenszerű mozgás, amint az az alábbi ábrán látható. 
Ez a mozgás valójában nagyon gyors. Például a fémekben szobahőmérsékleten az elektronikus hőmozgás sebessége másodpercenként több száz kilométeres nagyságrendű!
Ha alaposan megnézzük ezt a véletlenszerű mozgást, azt találjuk, hogy az egyes részecskék mozgási iránya bármely pillanatban véletlenszerű. Ha ezeknek a részecskéknek a sebességvektorait összeadjuk, az eredmény majdnem nulla.
Most adjunk hozzá elektromos teret a vezetőhöz, és az elektron véletlenszerű mozgás alapján irányított mozgást hoz létre. Feltételezve, hogy az elektromos tér egy bizonyos ideig balra van, az elektronok mozgása a következőképpen néz ki. A vörös golyók fématomokat jelölnek a kristályrácson, a gyorsan mozgó pontok pedig a szabad elektronokat. 
Gyorsnak tűnik? Ez azért van, mert az elektronikus mozgás nagyon gyors! De valójában a véletlenszerű mozgás, amely ennek nagy részét teszi ki, nem járul hozzá az áramhoz. Ha a véletlenszerű mozgást kiküszöböljük, a többi pont olyan, mint az alábbi lassú pillantás.
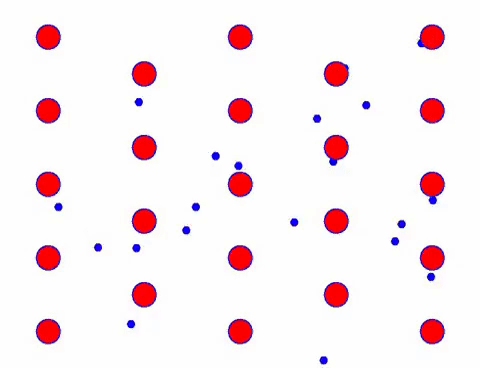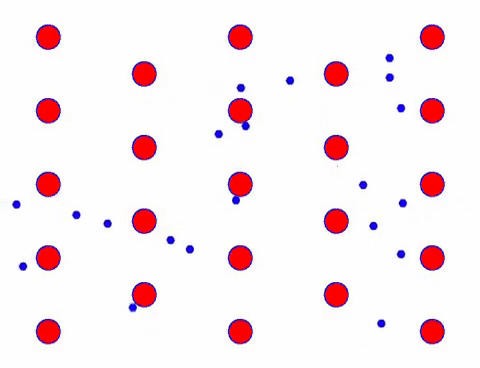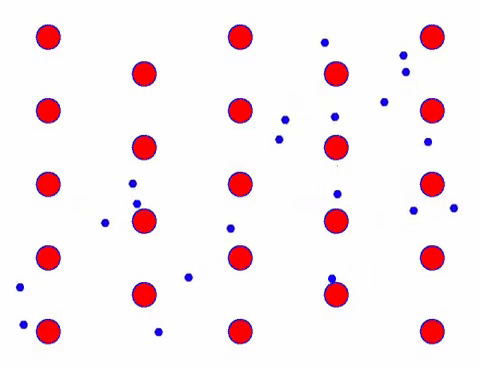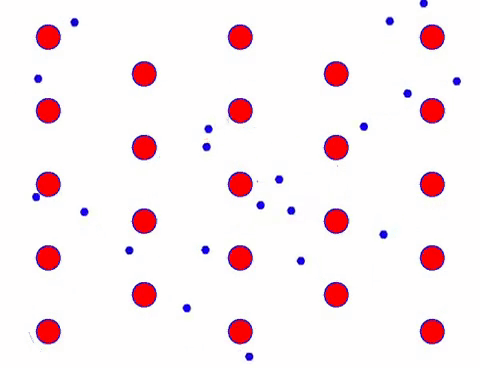
Valójában az elektronok iránymozgása sokkal lassabb, mint a hőmozgás sebessége. Az elektronoknak ezt a „csiszoló” mozgását sodródásnak vagy „sodródásnak” nevezik. Néha az elektronok ellenkező irányba futnak az atomokkal való ütközés miatt. De általában az elektronok egy irányba mozognak.
Ha az elektromos tér irányt változtat, az elektronsodródás iránya is megváltozik.
Ezért az ilyen irányú mozgás azt jelenti, hogy a vezetésben részt vevő összes elektron sebességének összege egy adott időpontban nem nulla, hanem általában egy bizonyos irányú. Ez az irány bármikor megváltoztatható, és ez a váltakozó áram esetében van így.
Ezért az áram nem annyira az elektromos töltés „iránymozgása”, mint inkább az elektromos töltés „kollektív mozgása”.
A vezetőben lévő áram nagyságát az áramerősség fejezi ki. Az áramerősséget a vezeték keresztmetszetén egységnyi idő alatt áthaladó villamos energia mennyiségeként határozzuk meg, azaz
Megtanultunk néhány olyan fizikai mennyiséget, amelyek tartalmazzák az „intenzitás” szót, mint például az elektromos tér intenzitása és a mágneses indukció intenzitása. Általában az egységnyi időre, egységnyi területre (vagy egységnyi térfogatra, egységnyi térszögre) vonatkozó felosztást jelentik. A jelenlegi intenzitásban szereplő „intenzitás” szó azonban nem tükrözi a terület jelenlegi felosztását.
Valójában egy másik fizikai mennyiség felelős az áram területenkénti elosztásáért, ez az áramsűrűség.
Mivel az elektromos áram lényege az elektromos töltés irányított mozgása, ezért az áramerősség és a sodródási sebesség között bizonyos kapcsolatnak kell lennie!
Ahhoz, hogy ezt az összefüggést megkapjuk, először egy fogalom-hordozó koncentrációt kell tisztáznunk, vagyis az egységnyi térfogatban lévő hordozók számát, amelyet fejez ki.
Feltételezzük, hogy a vezető keresztmetszete, a hordozókoncentrációja, a sodródási sebessége és a töltött töltése.
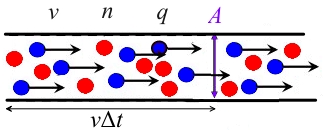
Ekkor a vezető töltése a felület bal oldalán van, és ezek a töltések egy bizonyos időn belül áthaladnak a felületen, így
Ez az áramerősség mikroszkopikus kifejezése.
Az áramsűrűség az áram területre való felosztása, tehát az áramsűrűség nagysága az, de vektorként van definiálva, az irány pedig a pozitív töltésű hordozók sodródási sebességvektorának iránya, tehát az elektronok sodródása a fém nyerhető ebből a sebességből, az alábbi példa szerint.
Vegyünk egy rézhuzalt, feltételezve, hogy minden rézatom egy elektront ad hordozóként. 1 mol réz van, térfogata, moláris tömege, sűrűsége, akkor a rézhuzal hordozókoncentrációja
Where is Avogadro’s constant. The density of copper is found, and the value obtained by substituting is about unit/cubic meter.
Feltételezve, hogy a rézhuzal sugara 0.8 mm, az átfolyó áram 15A, =1.6 C, és az elektronok sodródási sebességét a következőképpen számítjuk ki.
Látható, hogy az elektronok sodródási sebessége valóban nagyon kicsi.
Az áramkörök tanulmányozói számára a fenti az áram teljes definíciója.
De a fizikában az áram fenti definíciója valójában csak szűk definíció. Az általánosabb áramok nem korlátozódnak a vezetőkre, mindaddig, amíg az elektromos töltések mozgása áram. Például amikor egy hidrogénatom elektronjai az atommag körül mozognak, a pályáján elektromos áram keletkezik.

Tegyük fel, hogy az elektronikus töltés mértéke és a mozgás időtartama. Ekkor minden alkalommal olyan nagy mennyiségű töltés halad át a hurok bármely keresztmetszetén, így az áramerősség a periódus, a frekvencia és a szögsebesség összefüggésén alapul, és az áramerősség így is kifejezhető.
Egy másik példa, hogy egy feltöltött fémkorong a tengelye körül forogva szintén különböző sugarú hurokáramokat képez.

Ez a fajta áram nem normális vezetési áram, és nem képes Joule-hőt generálni! Nem tud valódi áramkört kialakítani.
Ellenkező esetben adna nekem egy számítást, hogy mennyi joule hőt termelnek másodpercenként a hidrogénatom elektronjai?
Valójában a vákuumban lévő áram nem teljesíti az Ohm-törvényt. Mivel a töltött részecskék vákuumban való mozgása által képződött elektromos áram esetében a hordozók nem ütköznek a fém rácsához hasonlóan, így a vákuumnak nincs ellenállása és vezetőképessége.
Az elektromos töltések mozgása elektromos áramot hoz létre, és maga az elektromos töltés gerjeszti az elektromos teret. Ebből könnyen lehet félreértés. Sokan ezért úgy gondolják, hogy az elektromos áramot alkotó töltött részecskék elektromos terét ki kell tárni. Valójában azonban az általános vezetőben lévő vezetési áramhoz a hordozók nagyszámú pozitív töltésű fémionból álló háttéren áramlanak, és maga a vezető semleges!
Ezt a fajta speciális áramot gyakran „egyenértékű áramnak” nevezzük. Az ekvivalens itt azt jelenti, hogy ugyanolyan alapon hoz létre mágneses teret, mint egy közönséges vezetési áram!
Emlékeztető: Ne keverje össze az „egyenértékű áramot” az „egyenértékű áramkörrel” az áramkörelemzés során
Valójában, amikor először tanulmányoztuk a mágneses teret, az elektromos áram Biot-Saffar törvényében az az általánosított elektromos áram volt, amely ezt az egyenértékű áramot tartalmazza. Természetesen a Maxwell-egyenletekben szereplő vezetési áram is az általánosított áramra vonatkozik.
Azok, akik tanulmányozták a fotoelektromos hatást, tudják, hogy amikor a fotoelektron a katódról az anódra sodródik, ha a levegő hatását figyelmen kívül hagyjuk, akkor ezt az áramot az elektromos töltések mozgása okozza a vákuumban, és nincs ellenállás, így Ohm törvénye nem korlátozza.
Tehát ez az egyetlen dolog az elektromos áramról a fizikában?
Nem! Két típusa is van, mégpedig a mágnesező áram és az eltolási áram.
Ez is két egyenértékű áram, amelyeket, ahogy a neve is sugallja, szintén a mágnesesség magyarázatára vezették be. Vagyis elszakadtak a jelenlegi „töltésmozgalom” alapvető jellemzőjétől!
Ez elképesztő! Nincs elektromos töltésmozgás, miért nevezhető tehát elektromos áramnak?
Ne aggódj, és lassan hallgass rám.
Nézzük először a mágnesező áramot.
Megállapították, hogy a mágnesességet az elektromosság mozgása okozza (egyelőre figyelmen kívül hagyva a mágnesességnek a spin belső tulajdonságaival való magyarázatát). A természetes mágnesesség magyarázata érdekében Ampere francia fizikus a „molekuláris keringés” hipotézisét terjesztette elő. 
Amint az alábbi ábrán látható, bármely atomnak vagy molekulának tekinthetünk olyan elektromos töltéssel, amely a középpont körül forog, és apró hurokáramot, azaz „molekuláris keringést” képez.
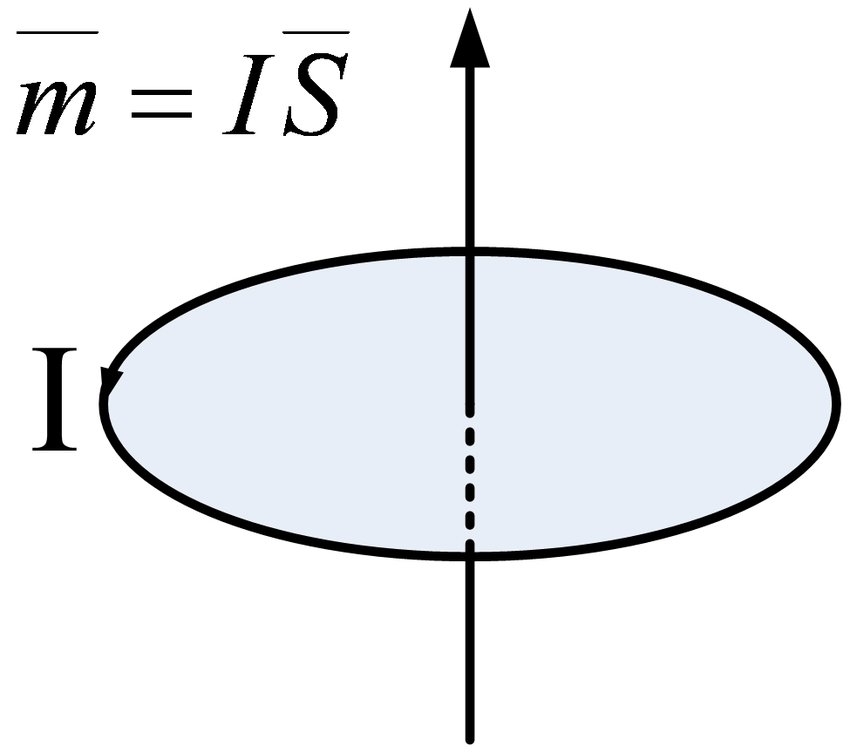
A törvény szerint, miszerint az elektromos áram gerjeszti a mágneses teret, ez a molekuláris cirkuláció egy fizikai mennyiséget hoz létre, amelyet mágneses momentumnak neveznek. Mérete a molekuláris keringés által bezárt terület szorozva a molekuláris cirkuláció ekvivalens áramával, iránya pedig jobb oldali spirális kapcsolatban van a keringés irányával, azaz
Nyilvánvaló, hogy a mágneses momentum iránya pontosan a keringő áram által alkotott mágneses tér iránya mentén van
. 
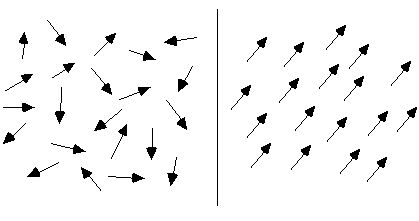
Normál körülmények között egy anyag molekuláris keringésének elrendezése kaotikus, így az anyag nem mágneses, ahogy az alábbi ábra bal oldalán látható. Ha külső mágneses térnek vannak kitéve, ezek a molekuláris cirkulációk megközelítőleg szépen elrendeződnek. Ahogy az alábbi ábra jobb oldalán is látható, mágneses momentumaik amennyire csak lehetséges, egy irányban helyezkednek el, akárcsak számtalan kis mágneses tű, amely összegyűjtve egy teljes mágneses mezőt alkot, és a belőlük álló teljes anyag mágnesessé válik.
Tegyük fel, hogy van egy hengeres mágnes, a belső molekuláris keringés szépen el van rendezve, és az egyes molekuláris keringés részei a mágnesszakasz szélén össze vannak kapcsolva, hogy nagy keringést alkossanak, amint az az alábbi ábrán látható. 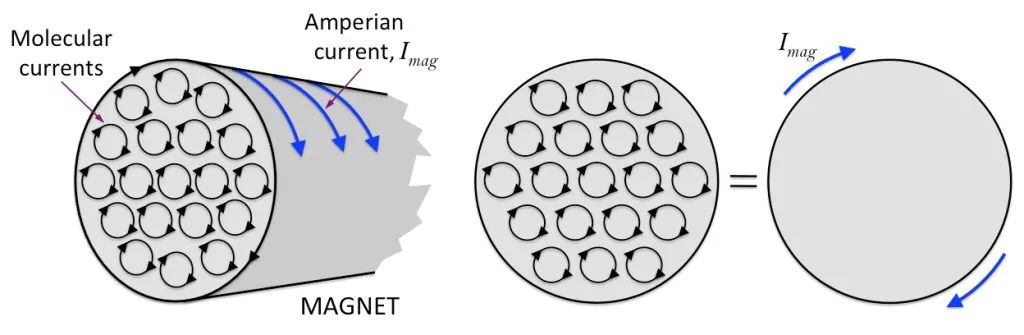
Ez alapján azt gondolhatjuk, hogy a rúdmágnes olyan, mint egy feszültség alatt álló mágnesszelep. Más szóval, a mágnes felületén egy láthatatlan áram van összegabalyodva! Ez a fajta áram nem csatlakoztatható és nem használható. A mágnes felületére korlátozódik. Nevezzük „kötőáramnak” vagy „mágnesező áramnak”.
Ezért a mágnesező áram áram, mert megegyezik a valódi elektromos töltések mozgása során keletkező árammal, amely ekvivalens módon képes mágneses teret generálni!
Nézzük meg még egyszer az elmozdulási áramot.
Az Ampere huroktétele szerint a mágneses térerősség integrálja zárt pályán egyenlő az áramsűrűség fluxusával bármely ezen út által határolt görbe felületen, vagyis ezt a tételt a matematikában Stokes-tételnek nevezik. Azt mondja meg, hogy egy vektor integrálja bármely zárt pálya mentén egyenlő kell legyen a görbületének fluxusával (itt) a zárt út által határolt bármely felületre.
Mivel matematikai tételről van szó, mindig helyesnek kell lennie, mert a matematika egy axiómákon alapuló logikai rendszer.
Ezért az Amper huroktételnek mindig érvényesülnie kell!
A tehetséges skót fizikus, Maxwell azonban felfedezte, hogy instabil áramkörrel szembesülve az Amper huroktétel ellentmondásos.

A tipikus instabil áram a kondenzátor töltése és kisütése során lép fel. Amint az alábbi ábrán látható, instabil áram van a kondenzátor töltési ideje alatt.
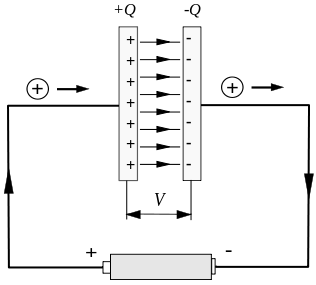
But the circuit is disconnected between the capacitor plates, which will cause a serious problem.
Tegyük fel, hogy egy zárt, a vezetéket megkerülő útvonalat tekintünk, ahogy az alábbi ábrán látható, a C-vel jelölt kör és a vele határolt íves felület tetszőlegesen kiválasztható. Az ábrán a maga C által körülzárt és a kondenzátoron keresztező körsík van kiválasztva. A bal oldali lemez ívelt felülete. 
A körfelület szerint látható, hogy az ívelt felület szerint, de a mágneses térerősség hurokintegráljaként kell meghatározni az értékét!
Hogyan kell csinálni?
Maxwell úgy véli, hogy az Ampere huroktételét meg kell állapítani. Most, hogy baj van, biztos azért, mert az áram egy részét korábban nem fedeztük fel, de létezik!
Szóval, hogyan lehet kideríteni az áram ezen részét?
Mivel a probléma a lemezek között van, kezdje a lemezek között.
Maxwell elemzése során megállapította, hogy a töltéstől vagy kisütéstől függetlenül a kondenzátorlemezek között mindig van egy fizikai mennyiség, amely szinkronban van az áram nagyságával és irányával. Ez az elektromos elmozdulásvektor fluxusának időbeli deriváltja, azaz eltolási áramként definiálható.
Ha úgy tekintjük, hogy ez a rész az áramnak az a része, amelyet korábban nem fedeztek fel, akkor a teljes áram most van. Ez azt jelenti, hogy bár a lemezek közötti áramkör megszakadt, az elektromos eltolási fluxus és az áram összegének deriváltja együttesen, mint egész , Mindenkor biztosítsa az áram folytonosságát.
Visszatérve az előző ellentmondáshoz, ma már tudjuk, hogy a Stokes-tétel követelményei szerint az áramsűrűség fluxusának számításakor zárt felületre az eltolási áram sűrűségét is figyelembe kell venni, vagyis a teljes amperhurkot. tétel tehát: Ennek az új aktuális komponensnek a „felfedezésével” megoldódik az Amper huroktétel válsága!
Az ok, amiért itt nem a „bevezetést”, hanem a „felfedezést” használjuk. Azt szeretném hangsúlyozni, hogy ez a fajta áram nem matematikai kompenzáció, hanem valós dolog, de korábban még nem fedezték fel.
Why does it exist in the first place? Because it acts as an electric current, like a conduction current, it excites a magnetic field equivalently, except that there is no movement of electric charges, no wire is required, and no Joule heat can be generated, so it has been ignored!
De valójában önmagában létezik, csak tartsa alacsony profilját, hangtalanul izgatta ott a mágneses teret állandóan!
Más szóval, amikor mágneses térrel nézünk szembe, az áram eredeti meghatározása túl szűk. Az elektromos áram lényege nem az elektromos töltés mozgása, hanem valami olyasmi legyen, ami képes gerjeszteni egy mágneses teret.
So far, the several forms of current have been introduced. They all exist objectively, and what they have in common is that all currents can equally excite the magnetic field.
