Wat is de elektrische stroom? Bedenk eerst, wat is de definitie van stroom die we hebben geleerd?

Heel eenvoudig, de gerichte beweging van geladen deeltjes in een geleider is een elektrische stroom.

Alleen wanneer een stof geladen deeltjes heeft die vrij kunnen bewegen, kan het elektrische stroom overbrengen, dat wil zeggen elektriciteit geleiden. Deze geladen deeltjes die deelnemen aan geleiding worden dragers genoemd. Voor metalen kunnen bijvoorbeeld alleen de buitenste elektronen van atomen als drager fungeren.

De “richtingsbeweging” in de definitie van elektrische stroom wordt vaak verkeerd begrepen. Veel mensen denken dat het verwijst naar beweging met een bepaalde richting, natuurlijk niet! Verandert de bewegingsrichting van de elektronen in het wisselstroomcircuit niet?

In feite is oriëntatielopen relatief aan “willekeurige bewegingen”!

Omdat elektronen microscopisch kleine deeltjes zijn, moeten ze de hele tijd in thermische beweging zijn. Thermische beweging is een willekeurige beweging, zoals weergegeven in de onderstaande afbeelding.

Deze beweging is eigenlijk heel snel. In metalen bij kamertemperatuur bijvoorbeeld, is de snelheid van elektronische thermische beweging in de orde van honderden kilometers per seconde!

Als je goed naar deze willekeurige beweging kijkt, zul je zien dat de bewegingsrichting van elk deeltje op elk moment willekeurig is. Als je de snelheidsvectoren van deze deeltjes bij elkaar optelt, is het resultaat bijna nul.

Voeg nu een elektrisch veld toe aan de geleider en het elektron superponeert een gerichte beweging op basis van willekeurige beweging. Ervan uitgaande dat het elektrische veld gedurende een bepaalde tijd naar links is, ziet de beweging van de elektronen er als volgt uit. De rode ballen vertegenwoordigen metaalatomen op het kristalrooster en de snel bewegende stippen vertegenwoordigen vrije elektronen.

Ziet het er snel uit? Dat komt omdat elektronische beweging echt snel is! Maar in feite draagt ​​de willekeurige beweging, die er een groot deel van uitmaakt, niet bij aan de stroom. Wanneer de willekeurige beweging wordt geëlimineerd, is de rest net als de langzame blik hieronder.

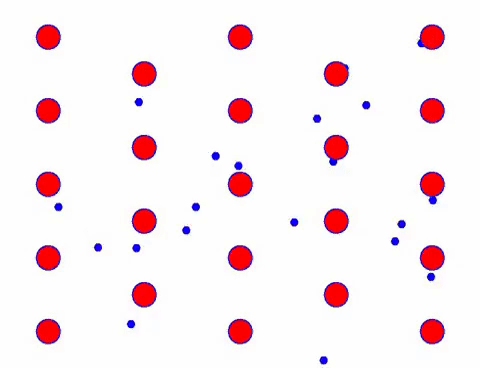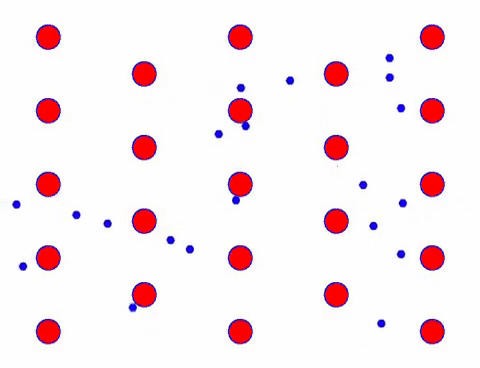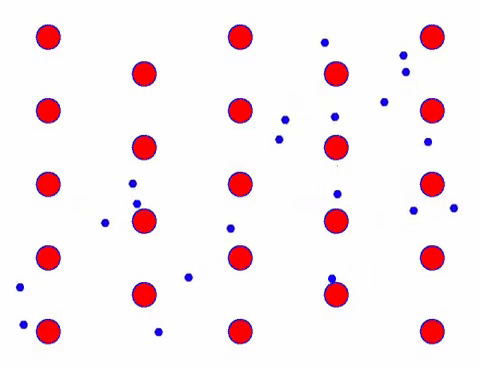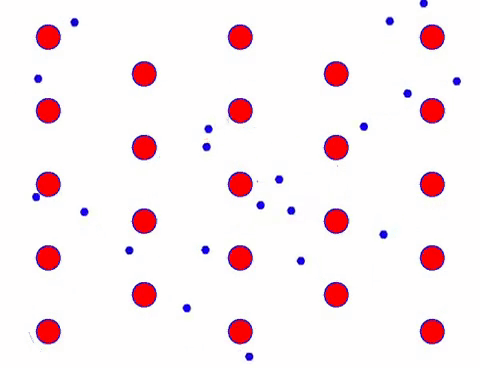
Inderdaad, de directionele beweging van elektronen is veel langzamer dan de snelheid van thermische beweging. Deze “slijpende” beweging van elektronen wordt drift of “drift” genoemd. Soms zullen elektronen in de tegenovergestelde richting lopen vanwege botsingen met atomen. Maar over het algemeen bewegen elektronen in één richting.

Als het elektrische veld van richting verandert, verandert ook de richting van de elektronendrift.

Daarom betekent dit soort gerichte beweging dat de som van de snelheden van alle elektronen die op een bepaald moment aan de geleiding deelnemen, niet nul is, maar in het algemeen in een bepaalde richting. Deze richting kan op elk moment worden gewijzigd, en dat is het geval bij wisselstroom.

Daarom is stroom niet zozeer de “richtingsbeweging” van elektrische lading, maar de “collectieve beweging” van elektrische lading.

De grootte van de stroom in de geleider wordt uitgedrukt door de stroomsterkte. De stroomsterkte wordt gedefinieerd als de hoeveelheid elektriciteit die in een tijdseenheid door de doorsnede van de geleider gaat, namelijk:

We hebben enkele fysieke grootheden geleerd die het woord “intensiteit” bevatten, zoals de intensiteit van het elektrische veld en de magnetische inductie-intensiteit. Ze vertegenwoordigen over het algemeen de verdeling per tijdseenheid, oppervlakte-eenheid (of eenheidsvolume, eenheidshoek). Het woord ‘intensiteit’ in de huidige intensiteit geeft echter niet de huidige verdeling van het gebied weer.

In feite is een andere fysieke grootheid verantwoordelijk voor de verdeling van de stroom naar het gebied, namelijk de stroomdichtheid.

Aangezien de essentie van elektrische stroom de directionele beweging van elektrische lading is, moet er een bepaalde relatie zijn tussen stroomintensiteit en driftsnelheid!

Om deze relatie te verkrijgen, moeten we eerst een concept-dragerconcentratie verduidelijken, dat wil zeggen, het aantal dragers in een volume-eenheid, uitgedrukt door .

Aangenomen wordt dat de doorsnede van de geleider is, de concentratie van de drager is, de driftsnelheid is, en de geladen lading is.

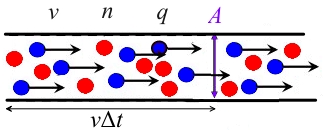
Dan is de lading in de geleider aan de linkerkant van het oppervlak, en deze ladingen zullen binnen een bepaalde tijd door het oppervlak gaan, dus

Dit is een microscopische uitdrukking van de stroomsterkte.

Stroomdichtheid is de verdeling van stroom naar gebied, dus de grootte van stroomdichtheid is, maar het wordt gedefinieerd als een vector, en de richting is de richting van de driftsnelheidsvector van de positief geladen dragers, dus de drift van elektronen in de metaal kan uit deze Speed ​​worden verkregen, als voorbeeld hieronder.

Beschouw een koperdraad, ervan uitgaande dat elk koperatoom een ​​elektron als drager bijdraagt. Er is 1 mol koper, het volume is, de molmassa is, de dichtheid is, dan is de dragerconcentratie van de koperdraad

Waar is de constante van Avogadro. De dichtheid van koper wordt gevonden en de waarde die wordt verkregen door vervanging is ongeveer eenheid / kubieke meter.

Ervan uitgaande dat de straal van de koperdraad 0.8 mm is, is de stroom die vloeit 15 A, = 1.6 C, en wordt de driftsnelheid van elektronen berekend als

Het is te zien dat de driftsnelheid van elektronen inderdaad erg klein is.

Voor degenen die circuits bestuderen, is het bovenstaande de volledige definitie van stroom.

Maar in de natuurkunde is de bovenstaande definitie van stroom eigenlijk slechts een enge definitie. Meer algemene stromen zijn niet beperkt tot geleiders, zolang de beweging van elektrische ladingen stroom is. Wanneer bijvoorbeeld de elektronen van een waterstofatoom rond de kern bewegen, wordt er een elektrische stroom gevormd in zijn baan.

Stel dat de hoeveelheid elektronische lading is en de bewegingsperiode is. Elke keer dat dat verstrijkt, gaat er zo’n grote hoeveelheid lading door een dwarsdoorsnede van de lus, dus de stroomintensiteit is gebaseerd op de relatie tussen periode, frequentie en hoeksnelheid, en de stroom kan ook worden uitgedrukt als

Een ander voorbeeld: een geladen metalen schijf, die om zijn as draait, vormt ook lusstromen met verschillende stralen.

Dit soort stroom is geen normale geleidingsstroom en kan geen Joule-warmte genereren! Kan geen echt circuit vormen.

Zou je me anders een berekening kunnen geven van hoeveel joule-warmte per seconde wordt gegenereerd door de elektronen van het waterstofatoom?

In feite voldoet de stroom in vacuüm niet aan de wet van Ohm. Omdat voor de elektrische stroom die wordt gevormd door de beweging van geladen deeltjes in het vacuüm, de dragers niet in botsing komen zoals het rooster in het metaal, dus het vacuüm heeft geen weerstand en geen geleiding.

De beweging van elektrische ladingen genereert elektrische stroom en de elektrische lading zelf wekt het elektrische veld op. Dit is gemakkelijk om een ​​misverstand te veroorzaken. Veel mensen denken daarom dat het elektrische veld van de geladen deeltjes die de elektrische stroom vormen, moet worden blootgelegd. Maar in feite, voor de geleidingsstroom in een algemene geleider, stromen dragers op een achtergrond die bestaat uit een groot aantal positief geladen metaalionen, en de geleider zelf is neutraal!

We noemen dit soort speciale stromen vaak een “equivalente stroom”. Het equivalent betekent hier dat het een magnetisch veld genereert op dezelfde basis als een gewone geleidingsstroom!

Herinnering: verwar de “equivalente stroom” hier niet met het “equivalente circuit” in circuitanalyse

In feite, toen we het magnetische veld voor het eerst bestudeerden, was de elektrische stroom in de wet van Biot-Saffar de gegeneraliseerde elektrische stroom die deze equivalente stroom bevatte. Natuurlijk verwijst de geleidingsstroom in de vergelijkingen van Maxwell ook naar de gegeneraliseerde stroom.

Degenen die het foto-elektrisch effect hebben bestudeerd, weten dat wanneer het foto-elektron van de kathode naar de anode drijft, als de invloed van lucht wordt genegeerd, deze stroom wordt veroorzaakt door de beweging van elektrische ladingen in het vacuüm, en er is geen weerstand, dus het wordt niet beperkt door de wet van Ohm.

Dus, is dit het enige over elektrische stroom in de natuurkunde?

Nee! Er zijn ook twee soorten, namelijk magnetiserende stroom en verplaatsingsstroom.

Het zijn ook twee equivalente stromen, die, zoals de naam al doet vermoeden, ook worden geïntroduceerd om magnetisme te verklaren. Met andere woorden, ze hebben zich losgemaakt van het basiskenmerk van de huidige “ladingsbeweging”!

Dat is geweldig! Er is geen elektrische ladingsbeweging, dus waarom kan het een elektrische stroom worden genoemd?

Maak je geen zorgen en luister langzaam naar me.

Laten we eerst naar de magnetiserende stroom kijken.

Gevonden werd dat magnetisme wordt veroorzaakt door de beweging van elektriciteit (voorlopig de verklaring van magnetisme door de intrinsieke eigenschappen van spin buiten beschouwing gelaten). Om natuurlijk magnetisme te verklaren, bracht de Franse natuurkundige Ampere de hypothese van “moleculaire circulatie” naar voren.

Zoals te zien is in de onderstaande afbeelding, kan elk atoom of molecuul worden beschouwd als een elektrische lading die rond het centrum draait en een kleine lusstroom vormt, dat wil zeggen “moleculaire circulatie”.

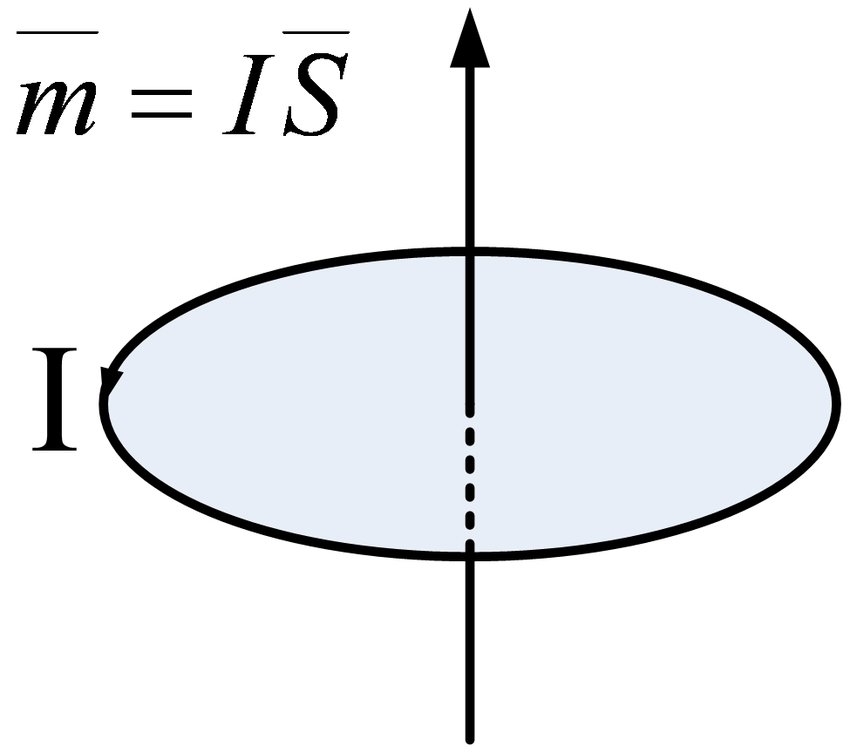
Volgens de wet dat de elektrische stroom het magnetische veld opwekt, zal deze moleculaire circulatie een fysieke hoeveelheid produceren die magnetisch moment wordt genoemd. Zijn grootte is het gebied dat wordt ingesloten door de moleculaire circulatie vermenigvuldigd met de equivalente stroom van de moleculaire circulatie, en zijn richting is in een rechtshandige spiraalrelatie met de richting van de circulatie, namelijk

Uiteraard is de richting van het magnetische moment precies in de richting van het magnetische veld gevormd door de circulatiestroom

.

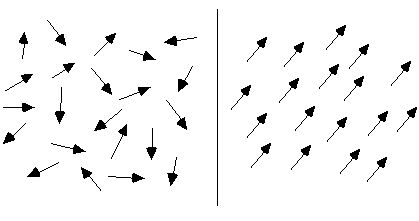
Onder normale omstandigheden is de ordening van de moleculaire circulatie van een stof chaotisch, dus de stof is niet magnetisch, zoals links in onderstaande figuur te zien is. Wanneer ze worden blootgesteld aan een extern magnetisch veld, zullen deze moleculaire circulaties ongeveer netjes worden gerangschikt. Zoals te zien is aan de rechterkant van de onderstaande afbeelding, zijn hun magnetische momenten zoveel mogelijk in één richting gerangschikt, net als talloze kleine magnetische naalden die samen een totaal magnetisch veld vormen, en het hele materiaal dat daaruit bestaat, wordt magnetisch.

Stel dat er een cilindrische magneet is, de binnenste moleculaire circulatie is netjes gerangschikt en de secties van elke moleculaire circulatie aan de rand van de magneetsectie zijn met elkaar verbonden om een ​​grote circulatie te vormen, zoals weergegeven in de onderstaande afbeelding.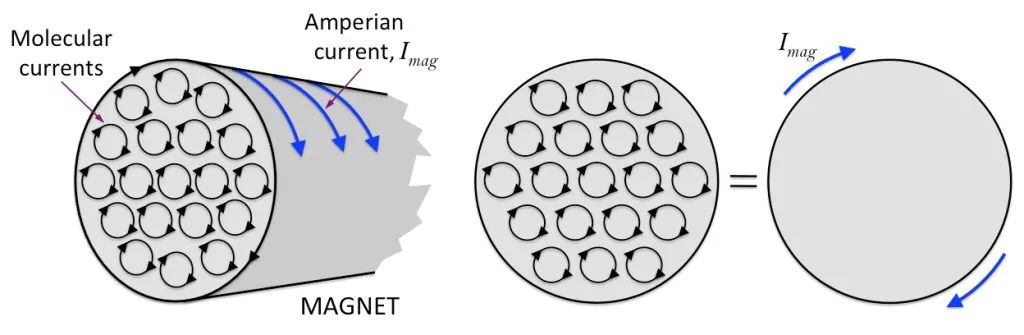

Op basis hiervan kunnen we denken dat een staafmagneet is als een bekrachtigde solenoïde. Met andere woorden, er is een onzichtbare stroom verstrikt op het oppervlak van de magneet! Dit soort stroom kan niet worden aangesloten en gebruikt. Het is beperkt tot het oppervlak van de magneet. We noemen het “bindstroom” of “magnetiserende stroom”.

Daarom is de magnetiserende stroom een ​​stroom, omdat deze dezelfde is als de stroom die wordt gevormd door de beweging van echte elektrische ladingen, die op equivalente wijze een magnetisch veld kunnen genereren!

Laten we nog eens naar de verplaatsingsstroom kijken.

Volgens de lusstelling van Ampere is de integraal van de magnetische veldsterkte op een gesloten pad gelijk aan de flux van de stroomdichtheid op elk gekromd oppervlak dat door dit pad wordt begrensd, dat wil zeggen dat deze stelling in de wiskunde de stelling van Stokes wordt genoemd. Het vertelt ons dat de integraal van een vector langs een gesloten pad gelijk moet zijn aan de flux van zijn krul (hier) naar een oppervlak dat wordt begrensd door het gesloten pad.

Omdat het een wiskundige stelling is, moet het altijd correct zijn, omdat wiskunde een logisch systeem is dat gebaseerd is op axioma’s.

Daarom moet de Ampere Loop Theorema altijd gelden!

De getalenteerde Schotse natuurkundige Maxwell ontdekte echter dat de stelling van de Ampere-lus tegenstrijdig was wanneer hij werd geconfronteerd met een onstabiel stroomcircuit.

De typische onstabiele stroom treedt op tijdens het laden en ontladen van de condensator. Zoals te zien is in de onderstaande afbeelding, is er een onstabiele stroom tijdens de korte oplaadperiode van de condensator.

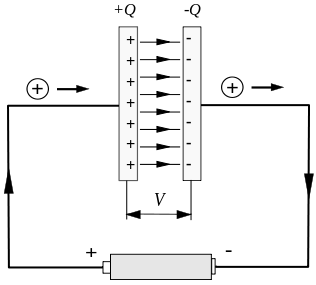
Maar het circuit is losgekoppeld tussen de condensatorplaten, wat een serieus probleem zal veroorzaken.

Stel dat we een gesloten pad beschouwen dat de draad omzeilt, zoals weergegeven in de onderstaande afbeelding, de cirkel gemarkeerd met C, en het gebogen oppervlak daarmee als de grens kan willekeurig worden gekozen. In de figuur is het cirkelvormige vlak omsloten door C zelf en over de condensator geselecteerd. Het gebogen oppervlak van de linkerplaat.

Volgens het cirkelvormige oppervlak kan worden gezien dat volgens het gebogen oppervlak, maar als een lusintegraal van de magnetische veldsterkte, de waarde ervan moet worden bepaald!

Hoe doe je?

Maxwell is van mening dat de lusstelling van Ampere moet worden vastgesteld. Nu er een probleem is, moet het zijn omdat een deel van de stroom niet eerder door ons is ontdekt, maar het bestaat wel!

Dus, hoe kom je dit deel van de stroom te weten?

Aangezien het probleem zich tussen de platen bevindt, begint u tussen de platen.

Door analyse ontdekte Maxwell dat er, ongeacht het laden of ontladen, te allen tijde een fysieke hoeveelheid tussen de condensatorplaten is die gesynchroniseerd is met de grootte en richting van de stroom. Het is de tijdsafgeleide van de flux van de elektrische verplaatsingsvector, dat wil zeggen, het wordt gedefinieerd als de verplaatsingsstroom.

Als men ervan uitgaat dat dit deel van de stroom het deel van de stroom is dat nog niet eerder is ontdekt, dan is de volledige stroom nu. Dat wil zeggen, hoewel het circuit tussen de platen is losgekoppeld, zorgt de afgeleide van de elektrische verplaatsingsflux en de som van de stroom samen, als geheel, te allen tijde voor de continuïteit van de stroom.

Terugkomend op de vorige tegenstrijdigheid, weten we nu dat, volgens de vereisten van de stelling van Stokes, bij het berekenen van de flux van stroomdichtheid voor een gesloten oppervlak, ook de dichtheid van verplaatsingsstroom moet worden overwogen, dat wil zeggen, de volledige ampèrelus stelling is daarom: Door deze nieuwe huidige component te “ontdekken”, is de crisis van de Ampere Loop-stelling opgelost!

De reden waarom “introductie” hier niet wordt gebruikt, maar “ontdekking” hier. Wat ik wil benadrukken is dat dit soort stroom geen wiskundige compensatie is, maar een reëel iets, maar het is nog niet eerder ontdekt.

Waarom bestaat het in de eerste plaats? Omdat het werkt als een elektrische stroom, zoals een geleidingsstroom, wekt het een magnetisch veld op equivalente wijze op, behalve dat er geen beweging van elektrische ladingen is, er geen draad nodig is en er geen Joule-warmte kan worden gegenereerd, dus het is genegeerd!

Maar het bestaat eigenlijk op zichzelf, houd je onopvallend, het is de hele tijd stil het magnetische veld daar aan het opwinden!

Met andere woorden, wanneer we geconfronteerd worden met een magnetisch veld, is de oorspronkelijke definitie van stroom te smal. De essentie van elektrische stroom is niet de beweging van elektrische lading, het zou iets moeten zijn dat een magnetisch veld kan opwekken.

Tot nu toe zijn de verschillende vormen van stroom geïntroduceerd. Ze bestaan ​​allemaal objectief, en wat ze gemeen hebben, is dat alle stromen het magnetische veld in gelijke mate kunnen opwekken.