ਬਿਜਲੀ ਦਾ ਕਰੰਟ ਕੀ ਹੈ? ਪਹਿਲਾਂ ਯਾਦ ਕਰੋ, ਅਸੀਂ ਸਿੱਖਿਆ ਹੈ ਕਿ ਵਰਤਮਾਨ ਦੀ ਪਰਿਭਾਸ਼ਾ ਕੀ ਹੈ?

ਬਿਲਕੁਲ ਸਧਾਰਨ ਰੂਪ ਵਿੱਚ, ਇੱਕ ਕੰਡਕਟਰ ਵਿੱਚ ਚਾਰਜ ਕੀਤੇ ਕਣਾਂ ਦੀ ਦਿਸ਼ਾਤਮਕ ਗਤੀ ਇੱਕ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਹੈ।

ਕੇਵਲ ਜਦੋਂ ਕਿਸੇ ਪਦਾਰਥ ਵਿੱਚ ਚਾਰਜ ਕੀਤੇ ਕਣ ਹੁੰਦੇ ਹਨ ਜੋ ਸੁਤੰਤਰ ਤੌਰ ‘ਤੇ ਘੁੰਮ ਸਕਦੇ ਹਨ, ਇਹ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਨੂੰ ਪ੍ਰਸਾਰਿਤ ਕਰ ਸਕਦਾ ਹੈ – ਯਾਨੀ ਬਿਜਲੀ ਦਾ ਸੰਚਾਲਨ ਕਰ ਸਕਦਾ ਹੈ। ਇਹ ਚਾਰਜ ਕੀਤੇ ਕਣ ਜੋ ਸੰਚਾਲਨ ਵਿੱਚ ਹਿੱਸਾ ਲੈਂਦੇ ਹਨ ਉਨ੍ਹਾਂ ਨੂੰ ਕੈਰੀਅਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਧਾਤਾਂ ਲਈ, ਉਦਾਹਰਨ ਲਈ, ਪਰਮਾਣੂਆਂ ਦੇ ਸਿਰਫ਼ ਬਾਹਰੀ ਇਲੈਕਟ੍ਰੋਨ ਹੀ ਕੈਰੀਅਰ ਵਜੋਂ ਕੰਮ ਕਰ ਸਕਦੇ ਹਨ।

ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਦੀ ਪਰਿਭਾਸ਼ਾ ਵਿੱਚ “ਦਿਸ਼ਾਤਮਕ ਗਤੀ” ਨੂੰ ਅਕਸਰ ਗਲਤ ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ। ਬਹੁਤ ਸਾਰੇ ਲੋਕ ਸੋਚਦੇ ਹਨ ਕਿ ਇਹ ਇੱਕ ਖਾਸ ਦਿਸ਼ਾ ਦੇ ਨਾਲ ਅੰਦੋਲਨ ਦਾ ਹਵਾਲਾ ਦਿੰਦਾ ਹੈ, ਬਿਲਕੁਲ ਨਹੀਂ! ਕੀ AC ਸਰਕਟ ਵਿੱਚ ਇਲੈਕਟ੍ਰੌਨਾਂ ਦੀ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਨਹੀਂ ਬਦਲਦੀ?

ਵਾਸਤਵ ਵਿੱਚ, ਓਰੀਐਂਟੀਅਰਿੰਗ “ਬੇਤਰਤੀਬ ਅੰਦੋਲਨ” ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ!

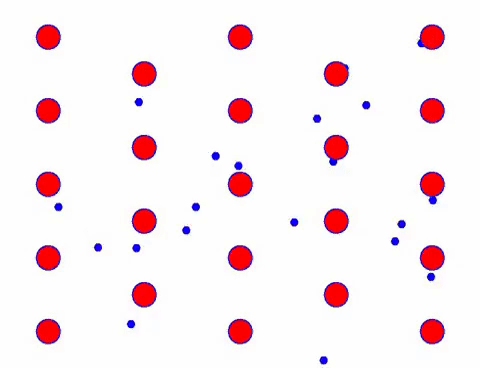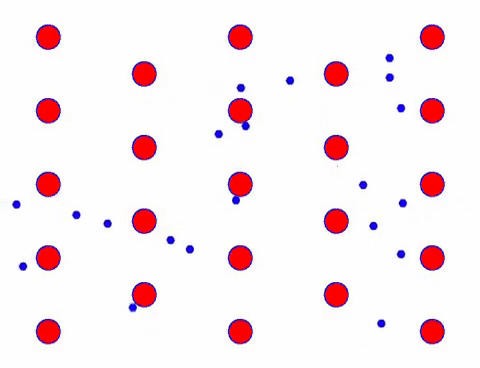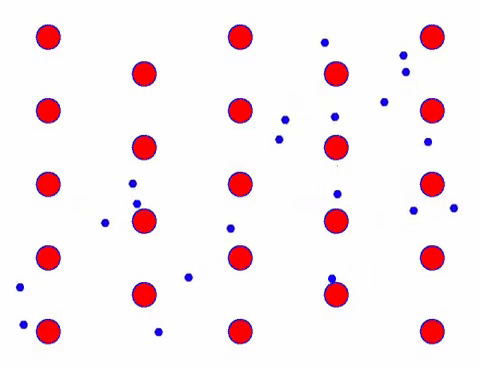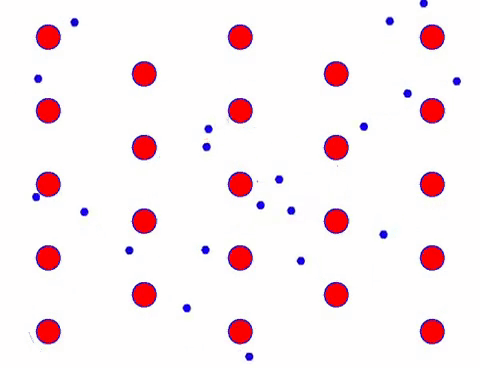
ਕਿਉਂਕਿ ਇਲੈਕਟ੍ਰੌਨ ਸੂਖਮ ਕਣ ਹਨ, ਉਹਨਾਂ ਨੂੰ ਹਰ ਸਮੇਂ ਥਰਮਲ ਮੋਸ਼ਨ ਵਿੱਚ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ। ਥਰਮਲ ਮੋਸ਼ਨ ਇੱਕ ਬੇਤਰਤੀਬ ਗਤੀ ਹੈ, ਜਿਵੇਂ ਕਿ ਹੇਠਾਂ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ।

ਇਹ ਅੰਦੋਲਨ ਅਸਲ ਵਿੱਚ ਬਹੁਤ ਤੇਜ਼ ਹੈ. ਉਦਾਹਰਨ ਲਈ, ਕਮਰੇ ਦੇ ਤਾਪਮਾਨ ‘ਤੇ ਧਾਤਾਂ ਵਿੱਚ, ਇਲੈਕਟ੍ਰਾਨਿਕ ਥਰਮਲ ਅੰਦੋਲਨ ਦੀ ਗਤੀ ਸੈਂਕੜੇ ਕਿਲੋਮੀਟਰ ਪ੍ਰਤੀ ਸਕਿੰਟ ਦੇ ਕ੍ਰਮ ‘ਤੇ ਹੁੰਦੀ ਹੈ!

ਜੇ ਤੁਸੀਂ ਇਸ ਬੇਤਰਤੀਬ ਗਤੀ ਨੂੰ ਨੇੜਿਓਂ ਦੇਖਦੇ ਹੋ, ਤਾਂ ਤੁਸੀਂ ਦੇਖੋਗੇ ਕਿ ਹਰੇਕ ਕਣ ਦੀ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਕਿਸੇ ਵੀ ਪਲ ਬੇਤਰਤੀਬ ਹੈ। ਜੇਕਰ ਤੁਸੀਂ ਇਹਨਾਂ ਕਣਾਂ ਦੇ ਵੇਗ ਵੈਕਟਰਾਂ ਨੂੰ ਜੋੜਦੇ ਹੋ, ਤਾਂ ਨਤੀਜਾ ਲਗਭਗ ਜ਼ੀਰੋ ਹੁੰਦਾ ਹੈ।

ਹੁਣ ਕੰਡਕਟਰ ਵਿੱਚ ਇੱਕ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਜੋੜੋ, ਅਤੇ ਇਲੈਕਟ੍ਰੌਨ ਬੇਤਰਤੀਬ ਗਤੀ ਦੇ ਅਧਾਰ ‘ਤੇ ਇੱਕ ਦਿਸ਼ਾ-ਨਿਰਦੇਸ਼ ਅੰਦੋਲਨ ਨੂੰ ਉੱਚਿਤ ਕਰਦਾ ਹੈ। ਇਹ ਮੰਨਦੇ ਹੋਏ ਕਿ ਇਲੈਕਟ੍ਰੋਨ ਫੀਲਡ ਇੱਕ ਨਿਸ਼ਚਿਤ ਸਮੇਂ ਲਈ ਖੱਬੇ ਪਾਸੇ ਹੈ, ਇਲੈਕਟ੍ਰੌਨਾਂ ਦੀ ਗਤੀ ਹੇਠ ਲਿਖੇ ਵਰਗੀ ਦਿਖਾਈ ਦਿੰਦੀ ਹੈ। ਲਾਲ ਗੇਂਦਾਂ ਕ੍ਰਿਸਟਲ ਜਾਲੀ ‘ਤੇ ਧਾਤ ਦੇ ਪਰਮਾਣੂਆਂ ਨੂੰ ਦਰਸਾਉਂਦੀਆਂ ਹਨ, ਅਤੇ ਤੇਜ਼ ਚਲਦੀਆਂ ਬਿੰਦੀਆਂ ਮੁਫ਼ਤ ਇਲੈਕਟ੍ਰੌਨਾਂ ਨੂੰ ਦਰਸਾਉਂਦੀਆਂ ਹਨ।

ਕੀ ਇਹ ਤੇਜ਼ੀ ਨਾਲ ਦਿਖਾਈ ਦਿੰਦਾ ਹੈ? ਇਹ ਇਸ ਲਈ ਹੈ ਕਿਉਂਕਿ ਇਲੈਕਟ੍ਰਾਨਿਕ ਅੰਦੋਲਨ ਅਸਲ ਵਿੱਚ ਤੇਜ਼ ਹੈ! ਪਰ ਵਾਸਤਵ ਵਿੱਚ, ਬੇਤਰਤੀਬ ਗਤੀ, ਜੋ ਇਸਦਾ ਇੱਕ ਵੱਡਾ ਅਨੁਪਾਤ ਹੈ, ਵਰਤਮਾਨ ਵਿੱਚ ਯੋਗਦਾਨ ਨਹੀਂ ਪਾਉਂਦੀ ਹੈ। ਜਦੋਂ ਬੇਤਰਤੀਬ ਗਤੀ ਨੂੰ ਖਤਮ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਬਾਕੀ ਹੇਠਾਂ ਹੌਲੀ ਦਿੱਖ ਵਾਂਗ ਹੀ ਹੁੰਦਾ ਹੈ।

ਦਰਅਸਲ, ਇਲੈਕਟ੍ਰੌਨਾਂ ਦੀ ਦਿਸ਼ਾਤਮਕ ਗਤੀ ਥਰਮਲ ਅੰਦੋਲਨ ਦੀ ਗਤੀ ਨਾਲੋਂ ਬਹੁਤ ਹੌਲੀ ਹੁੰਦੀ ਹੈ। ਇਲੈਕਟ੍ਰੌਨਾਂ ਦੀ ਇਸ “ਪੀਸਣ” ਦੀ ਗਤੀ ਨੂੰ ਡ੍ਰਾਈਫਟ ਜਾਂ “ਡ੍ਰਿਫਟ” ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਕਈ ਵਾਰ, ਪਰਮਾਣੂਆਂ ਨਾਲ ਟਕਰਾਉਣ ਕਾਰਨ ਇਲੈਕਟ੍ਰੌਨ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਚੱਲਣਗੇ। ਪਰ ਆਮ ਤੌਰ ‘ਤੇ, ਇਲੈਕਟ੍ਰੌਨ ਇੱਕ ਦਿਸ਼ਾ ਵਿੱਚ ਚਲੇ ਜਾਂਦੇ ਹਨ।

ਜੇਕਰ ਬਿਜਲਈ ਖੇਤਰ ਦਿਸ਼ਾ ਬਦਲਦਾ ਹੈ, ਤਾਂ ਇਲੈਕਟ੍ਰੋਨ ਡ੍ਰਾਈਫਟ ਦੀ ਦਿਸ਼ਾ ਵੀ ਬਦਲ ਜਾਵੇਗੀ।

ਇਸ ਲਈ, ਇਸ ਕਿਸਮ ਦੀ ਦਿਸ਼ਾ-ਨਿਰਦੇਸ਼ ਅੰਦੋਲਨ ਦਾ ਮਤਲਬ ਹੈ ਕਿ ਇੱਕ ਨਿਸ਼ਚਿਤ ਸਮੇਂ ‘ਤੇ ਸੰਚਾਲਨ ਵਿੱਚ ਭਾਗ ਲੈਣ ਵਾਲੇ ਸਾਰੇ ਇਲੈਕਟ੍ਰੌਨਾਂ ਦੀ ਗਤੀ ਦਾ ਜੋੜ ਜ਼ੀਰੋ ਨਹੀਂ ਹੈ, ਪਰ ਆਮ ਤੌਰ ‘ਤੇ ਇੱਕ ਖਾਸ ਦਿਸ਼ਾ ਵਿੱਚ ਹੁੰਦਾ ਹੈ। ਇਹ ਦਿਸ਼ਾ ਕਿਸੇ ਵੀ ਸਮੇਂ ਬਦਲੀ ਜਾ ਸਕਦੀ ਹੈ, ਅਤੇ ਇਹ ਬਦਲਵੇਂ ਕਰੰਟ ਦਾ ਮਾਮਲਾ ਹੈ।

ਇਸ ਲਈ, ਕਰੰਟ ਇਲੈਕਟ੍ਰਿਕ ਚਾਰਜ ਦੀ ਇੰਨੀ “ਦਿਸ਼ਾਵੀ ਗਤੀ” ਨਹੀਂ ਹੈ ਜਿੰਨਾ ਇਹ ਇਲੈਕਟ੍ਰਿਕ ਚਾਰਜ ਦੀ “ਸਮੂਹਿਕ ਗਤੀ” ਹੈ।

ਕੰਡਕਟਰ ਵਿੱਚ ਕਰੰਟ ਦੀ ਤੀਬਰਤਾ ਮੌਜੂਦਾ ਤੀਬਰਤਾ ਦੁਆਰਾ ਦਰਸਾਈ ਜਾਂਦੀ ਹੈ। ਮੌਜੂਦਾ ਤੀਬਰਤਾ ਨੂੰ ਇੱਕ ਯੂਨਿਟ ਸਮੇਂ ਵਿੱਚ ਕੰਡਕਟਰ ਦੇ ਕਰਾਸ-ਸੈਕਸ਼ਨ ਵਿੱਚੋਂ ਲੰਘਣ ਵਾਲੀ ਬਿਜਲੀ ਦੀ ਮਾਤਰਾ ਵਜੋਂ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਗਿਆ ਹੈ, ਅਰਥਾਤ

ਅਸੀਂ ਕੁਝ ਭੌਤਿਕ ਮਾਤਰਾਵਾਂ ਬਾਰੇ ਸਿੱਖਿਆ ਹੈ ਜਿਸ ਵਿੱਚ “ਤੀਬਰਤਾ” ਸ਼ਬਦ ਸ਼ਾਮਲ ਹੁੰਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਤੀਬਰਤਾ ਅਤੇ ਚੁੰਬਕੀ ਇੰਡਕਸ਼ਨ ਤੀਬਰਤਾ। ਉਹ ਆਮ ਤੌਰ ‘ਤੇ ਪ੍ਰਤੀ ਯੂਨਿਟ ਸਮਾਂ, ਇਕਾਈ ਖੇਤਰ (ਜਾਂ ਇਕਾਈ ਵਾਲੀਅਮ, ਇਕਾਈ ਠੋਸ ਕੋਣ) ਪ੍ਰਤੀ ਵੰਡ ਨੂੰ ਦਰਸਾਉਂਦੇ ਹਨ। ਹਾਲਾਂਕਿ, ਮੌਜੂਦਾ ਤੀਬਰਤਾ ਵਿੱਚ ਸ਼ਬਦ “ਤੀਬਰਤਾ” ਖੇਤਰ ਦੀ ਮੌਜੂਦਾ ਵੰਡ ਨੂੰ ਨਹੀਂ ਦਰਸਾਉਂਦਾ ਹੈ।

ਵਾਸਤਵ ਵਿੱਚ, ਇੱਕ ਹੋਰ ਭੌਤਿਕ ਮਾਤਰਾ ਖੇਤਰ ਵਿੱਚ ਕਰੰਟ ਦੀ ਵੰਡ ਲਈ ਜ਼ਿੰਮੇਵਾਰ ਹੈ, ਜੋ ਕਿ ਮੌਜੂਦਾ ਘਣਤਾ ਹੈ।

ਕਿਉਂਕਿ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਦਾ ਤੱਤ ਬਿਜਲਈ ਚਾਰਜ ਦੀ ਦਿਸ਼ਾਤਮਕ ਗਤੀ ਹੈ, ਇਸਲਈ ਕਰੰਟ ਦੀ ਤੀਬਰਤਾ ਅਤੇ ਵਹਿਣ ਦੀ ਗਤੀ ਵਿਚਕਾਰ ਇੱਕ ਖਾਸ ਸਬੰਧ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ!

ਇਸ ਸਬੰਧ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ, ਸਾਨੂੰ ਪਹਿਲਾਂ ਇੱਕ ਸੰਕਲਪ-ਕੈਰੀਅਰ ਇਕਾਗਰਤਾ ਨੂੰ ਸਪੱਸ਼ਟ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ, ਯਾਨੀ, ਇੱਕ ਯੂਨਿਟ ਵਾਲੀਅਮ ਵਿੱਚ ਕੈਰੀਅਰਾਂ ਦੀ ਸੰਖਿਆ, ਜਿਸਨੂੰ  ਦੁਆਰਾ ਦਰਸਾਇਆ ਗਿਆ ਹੈ।

ਇਹ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਕੰਡਕਟਰ ਕ੍ਰਾਸ ਸੈਕਸ਼ਨ ਹੈ, ਕੈਰੀਅਰ ਗਾੜ੍ਹਾਪਣ ਹੈ, ਵਹਿਣ ਦਾ ਵੇਗ ਹੈ, ਅਤੇ ਚਾਰਜ ਕੀਤਾ ਗਿਆ ਚਾਰਜ ਹੈ।

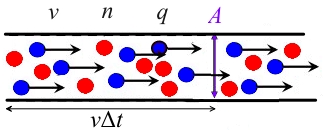
ਫਿਰ ਸਤਹ ਦੇ ਖੱਬੇ ਪਾਸੇ ਕੰਡਕਟਰ ਵਿੱਚ ਚਾਰਜ ਹੁੰਦਾ ਹੈ, ਅਤੇ ਇਹ ਚਾਰਜ ਇੱਕ ਨਿਸ਼ਚਿਤ ਸਮੇਂ ਦੇ ਅੰਦਰ ਸਤ੍ਹਾ ਵਿੱਚੋਂ ਲੰਘਣਗੇ, ਇਸ ਲਈ

ਇਹ ਮੌਜੂਦਾ ਤੀਬਰਤਾ ਦਾ ਸੂਖਮ ਪ੍ਰਗਟਾਵਾ ਹੈ।

ਵਰਤਮਾਨ ਘਣਤਾ ਖੇਤਰ ਵਿੱਚ ਕਰੰਟ ਦੀ ਵੰਡ ਹੈ, ਇਸਲਈ ਮੌਜੂਦਾ ਘਣਤਾ ਦੀ ਵਿਸ਼ਾਲਤਾ ਹੈ, ਪਰ ਇਸਨੂੰ ਇੱਕ ਵੈਕਟਰ ਵਜੋਂ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਗਿਆ ਹੈ, ਅਤੇ ਦਿਸ਼ਾ ਸਕਾਰਾਤਮਕ ਚਾਰਜ ਵਾਲੇ ਕੈਰੀਅਰਾਂ ਦੇ ਵਹਿਣ ਵੇਗ ਵੈਕਟਰ ਦੀ ਦਿਸ਼ਾ ਹੈ, ਇਸਲਈ ਵਿੱਚ ਇਲੈਕਟ੍ਰੌਨਾਂ ਦਾ ਵਹਿਣ ਧਾਤ ਨੂੰ ਇਸ ਸਪੀਡ ਤੋਂ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਹੇਠਾਂ ਦਿੱਤੀ ਉਦਾਹਰਣ ਵਜੋਂ।

ਇੱਕ ਤਾਂਬੇ ਦੀ ਤਾਰ ‘ਤੇ ਵਿਚਾਰ ਕਰੋ, ਇਹ ਮੰਨਦੇ ਹੋਏ ਕਿ ਹਰੇਕ ਤਾਂਬੇ ਦਾ ਪਰਮਾਣੂ ਇੱਕ ਕੈਰੀਅਰ ਵਜੋਂ ਇੱਕ ਇਲੈਕਟ੍ਰੌਨ ਦਾ ਯੋਗਦਾਨ ਪਾਉਂਦਾ ਹੈ। ਤਾਂਬੇ ਦਾ 1 ਮੋਲ ਹੈ, ਇਸਦਾ ਆਇਤਨ ਹੈ, ਮੋਲਰ ਪੁੰਜ ਹੈ, ਘਣਤਾ ਹੈ, ਫਿਰ ਤਾਂਬੇ ਦੀ ਤਾਰ ਦੀ ਕੈਰੀਅਰ ਸੰਘਣਤਾ ਹੈ

ਐਵੋਗਾਡਰੋ ਦਾ ਸਥਿਰ ਕਿੱਥੇ ਹੈ। ਤਾਂਬੇ ਦੀ ਘਣਤਾ ਪਾਈ ਜਾਂਦੀ ਹੈ, ਅਤੇ ਬਦਲ ਕੇ ਪ੍ਰਾਪਤ ਕੀਤਾ ਮੁੱਲ ਲਗਭਗ ਯੂਨਿਟ/ਘਣ ਮੀਟਰ ਹੈ।

ਇਹ ਮੰਨਦੇ ਹੋਏ ਕਿ ਤਾਂਬੇ ਦੀ ਤਾਰ ਦਾ ਘੇਰਾ 0.8mm ਹੈ, ਮੌਜੂਦਾ ਵਹਾਅ 15A, =1.6 C ਹੈ, ਅਤੇ ਇਲੈਕਟ੍ਰੌਨਾਂ ਦੇ ਵਹਿਣ ਦੀ ਵੇਗ ਦੀ ਗਣਨਾ ਕੀਤੀ ਜਾਂਦੀ ਹੈ

ਇਹ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਇਲੈਕਟ੍ਰੌਨਾਂ ਦੀ ਵਹਿਣ ਦੀ ਗਤੀ ਅਸਲ ਵਿੱਚ ਬਹੁਤ ਛੋਟੀ ਹੈ।

ਉਹਨਾਂ ਲਈ ਜੋ ਸਰਕਟਾਂ ਦਾ ਅਧਿਐਨ ਕਰਦੇ ਹਨ, ਉਪਰੋਕਤ ਕਰੰਟ ਦੀ ਪੂਰੀ ਪਰਿਭਾਸ਼ਾ ਹੈ।

ਪਰ ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ, ਵਰਤਮਾਨ ਦੀ ਉਪਰੋਕਤ ਪਰਿਭਾਸ਼ਾ ਅਸਲ ਵਿੱਚ ਸਿਰਫ ਇੱਕ ਤੰਗ ਪਰਿਭਾਸ਼ਾ ਹੈ। ਵਧੇਰੇ ਆਮ ਕਰੰਟ ਕੰਡਕਟਰਾਂ ਤੱਕ ਸੀਮਿਤ ਨਹੀਂ ਹਨ, ਜਿੰਨਾ ਚਿਰ ਇਲੈਕਟ੍ਰਿਕ ਚਾਰਜ ਦੀ ਗਤੀ ਕਰੰਟ ਹੈ। ਉਦਾਹਰਨ ਲਈ, ਜਦੋਂ ਇੱਕ ਹਾਈਡ੍ਰੋਜਨ ਪਰਮਾਣੂ ਦੇ ਇਲੈਕਟ੍ਰੋਨ ਨਿਊਕਲੀਅਸ ਦੇ ਦੁਆਲੇ ਘੁੰਮਦੇ ਹਨ, ਤਾਂ ਇਸਦੀ ਔਰਬਿਟ ਵਿੱਚ ਇੱਕ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਬਣਦਾ ਹੈ।

ਮੰਨ ਲਓ ਕਿ ਇਲੈਕਟ੍ਰਾਨਿਕ ਚਾਰਜ ਦੀ ਮਾਤਰਾ ਹੈ ਅਤੇ ਅੰਦੋਲਨ ਦੀ ਮਿਆਦ ਹੈ। ਫਿਰ ਹਰ ਵਾਰ ਜਦੋਂ ਬੀਤ ਜਾਂਦੀ ਹੈ, ਲੂਪ ਦੇ ਕਿਸੇ ਵੀ ਕਰਾਸ ਸੈਕਸ਼ਨ ਤੋਂ ਲੰਘਣ ਵਾਲੀ ਚਾਰਜ ਦੀ ਇੰਨੀ ਵੱਡੀ ਮਾਤਰਾ ਹੁੰਦੀ ਹੈ, ਇਸਲਈ ਵਰਤਮਾਨ ਤੀਬਰਤਾ ਪੀਰੀਅਡ, ਬਾਰੰਬਾਰਤਾ ਅਤੇ ਕੋਣੀ ਵੇਗ ਵਿਚਕਾਰ ਸਬੰਧ ‘ਤੇ ਅਧਾਰਤ ਹੁੰਦੀ ਹੈ, ਅਤੇ ਕਰੰਟ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਵੀ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ।

ਇੱਕ ਹੋਰ ਉਦਾਹਰਨ ਲਈ, ਇੱਕ ਚਾਰਜਡ ਮੈਟਲ ਡਿਸਕ, ਆਪਣੇ ਧੁਰੇ ਦੁਆਲੇ ਘੁੰਮਦੀ ਹੋਈ, ਵੱਖ-ਵੱਖ ਰੇਡੀਆਈ ਨਾਲ ਲੂਪ ਕਰੰਟ ਵੀ ਬਣਾਉਂਦੀ ਹੈ।

ਇਸ ਕਿਸਮ ਦਾ ਕਰੰਟ ਇੱਕ ਸਾਧਾਰਨ ਸੰਚਾਲਨ ਕਰੰਟ ਨਹੀਂ ਹੈ ਅਤੇ ਜੂਲ ਤਾਪ ਪੈਦਾ ਨਹੀਂ ਕਰ ਸਕਦਾ ਹੈ! ਇੱਕ ਅਸਲੀ ਸਰਕਟ ਨਹੀਂ ਬਣਾ ਸਕਦਾ.

ਨਹੀਂ ਤਾਂ, ਕੀ ਤੁਸੀਂ ਮੈਨੂੰ ਇਸ ਗੱਲ ਦੀ ਗਣਨਾ ਕਰੋਗੇ ਕਿ ਹਾਈਡ੍ਰੋਜਨ ਐਟਮ ਦੇ ਇਲੈਕਟ੍ਰੌਨਾਂ ਦੁਆਰਾ ਪ੍ਰਤੀ ਸਕਿੰਟ ਕਿੰਨੀ ਜੂਲ ਗਰਮੀ ਪੈਦਾ ਹੁੰਦੀ ਹੈ?

ਅਸਲ ਵਿੱਚ, ਵੈਕਿਊਮ ਵਿੱਚ ਕਰੰਟ ਓਮ ਦੇ ਨਿਯਮ ਨੂੰ ਪੂਰਾ ਨਹੀਂ ਕਰਦਾ। ਕਿਉਂਕਿ, ਵੈਕਿਊਮ ਵਿੱਚ ਚਾਰਜ ਕੀਤੇ ਕਣਾਂ ਦੀ ਗਤੀ ਨਾਲ ਬਣੇ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਲਈ, ਕੈਰੀਅਰ ਧਾਤ ਵਿੱਚ ਜਾਲੀ ਵਾਂਗ ਟਕਰਾਉਂਦੇ ਨਹੀਂ ਹਨ, ਇਸਲਈ ਵੈਕਿਊਮ ਦਾ ਕੋਈ ਵਿਰੋਧ ਅਤੇ ਕੋਈ ਸੰਚਾਲਨ ਨਹੀਂ ਹੁੰਦਾ ਹੈ।

ਇਲੈਕਟ੍ਰਿਕ ਚਾਰਜਾਂ ਦੀ ਗਤੀ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਪੈਦਾ ਕਰਦੀ ਹੈ, ਅਤੇ ਇਲੈਕਟ੍ਰਿਕ ਚਾਰਜ ਖੁਦ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਨੂੰ ਉਤੇਜਿਤ ਕਰਦਾ ਹੈ। ਇਹ ਗਲਤਫਹਿਮੀ ਪੈਦਾ ਕਰਨਾ ਆਸਾਨ ਹੈ। ਇਸ ਲਈ ਬਹੁਤ ਸਾਰੇ ਲੋਕ ਸੋਚਦੇ ਹਨ ਕਿ ਚਾਰਜ ਕੀਤੇ ਕਣਾਂ ਦਾ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਜੋ ਬਿਜਲੀ ਦਾ ਕਰੰਟ ਬਣਾਉਂਦੇ ਹਨ, ਦਾ ਪਰਦਾਫਾਸ਼ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ। ਪਰ ਅਸਲ ਵਿੱਚ, ਇੱਕ ਆਮ ਕੰਡਕਟਰ ਵਿੱਚ ਸੰਚਾਲਨ ਕਰੰਟ ਲਈ, ਕੈਰੀਅਰ ਇੱਕ ਵੱਡੀ ਗਿਣਤੀ ਵਿੱਚ ਸਕਾਰਾਤਮਕ ਚਾਰਜ ਵਾਲੇ ਧਾਤੂ ਆਇਨਾਂ ਦੀ ਬਣੀ ਬੈਕਗ੍ਰਾਉਂਡ ‘ਤੇ ਵਹਿਦੇ ਹਨ, ਅਤੇ ਕੰਡਕਟਰ ਖੁਦ ਨਿਰਪੱਖ ਹੁੰਦਾ ਹੈ!

ਅਸੀਂ ਅਕਸਰ ਇਸ ਕਿਸਮ ਦੇ ਵਿਸ਼ੇਸ਼ ਕਰੰਟ ਨੂੰ “ਬਰਾਬਰ ਕਰੰਟ” ਕਹਿੰਦੇ ਹਾਂ। ਇੱਥੇ ਬਰਾਬਰ ਦਾ ਮਤਲਬ ਹੈ ਕਿ ਇਹ ਇੱਕ ਸਾਧਾਰਨ ਸੰਚਾਲਨ ਕਰੰਟ ਦੇ ਸਮਾਨ ਅਧਾਰ ‘ਤੇ ਇੱਕ ਚੁੰਬਕੀ ਖੇਤਰ ਪੈਦਾ ਕਰਦਾ ਹੈ!

ਰੀਮਾਈਂਡਰ: ਇੱਥੇ “ਬਰਾਬਰ ਕਰੰਟ” ਨੂੰ ਸਰਕਟ ਵਿਸ਼ਲੇਸ਼ਣ ਵਿੱਚ “ਬਰਾਬਰ ਸਰਕਟ” ਨਾਲ ਉਲਝਾਓ ਨਾ।

ਵਾਸਤਵ ਵਿੱਚ, ਜਦੋਂ ਅਸੀਂ ਪਹਿਲੀ ਵਾਰ ਚੁੰਬਕੀ ਖੇਤਰ ਦਾ ਅਧਿਐਨ ਕੀਤਾ, ਤਾਂ ਬਾਇਓਟ-ਸੈਫਰ ਦੇ ਨਿਯਮ ਵਿੱਚ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਇੱਕ ਆਮ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਸੀ ਜਿਸ ਵਿੱਚ ਇਹ ਸਮਾਨ ਕਰੰਟ ਹੁੰਦਾ ਸੀ। ਬੇਸ਼ੱਕ, ਮੈਕਸਵੈਲ ਦੀਆਂ ਸਮੀਕਰਨਾਂ ਵਿੱਚ ਸੰਚਾਲਨ ਕਰੰਟ ਵੀ ਸਧਾਰਣ ਕਰੰਟ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ।

ਜਿਨ੍ਹਾਂ ਲੋਕਾਂ ਨੇ ਫੋਟੋਇਲੈਕਟ੍ਰਿਕ ਪ੍ਰਭਾਵ ਦਾ ਅਧਿਐਨ ਕੀਤਾ ਹੈ ਉਹ ਜਾਣਦੇ ਹਨ ਕਿ ਜਦੋਂ ਫੋਟੋਇਲੈਕਟ੍ਰੋਨ ਕੈਥੋਡ ਤੋਂ ਐਨੋਡ ਵੱਲ ਵਧਦਾ ਹੈ, ਜੇਕਰ ਹਵਾ ਦੇ ਪ੍ਰਭਾਵ ਨੂੰ ਨਜ਼ਰਅੰਦਾਜ਼ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਹ ਕਰੰਟ ਵੈਕਿਊਮ ਵਿੱਚ ਇਲੈਕਟ੍ਰਿਕ ਚਾਰਜ ਦੀ ਗਤੀ ਕਾਰਨ ਹੁੰਦਾ ਹੈ, ਅਤੇ ਕੋਈ ਵਿਰੋਧ ਨਹੀਂ ਹੁੰਦਾ, ਇਸ ਲਈ ਇਹ ਓਮ ਦੇ ਨਿਯਮ ਦੁਆਰਾ ਪ੍ਰਤਿਬੰਧਿਤ ਨਹੀਂ ਹੈ।

ਤਾਂ, ਕੀ ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਬਾਰੇ ਇਹੀ ਗੱਲ ਹੈ?

ਨਹੀਂ! ਦੋ ਕਿਸਮਾਂ ਵੀ ਹਨ, ਅਰਥਾਤ ਚੁੰਬਕੀ ਕਰੰਟ ਅਤੇ ਵਿਸਥਾਪਨ ਕਰੰਟ।

ਇਹ ਦੋ ਸਮਾਨ ਧਾਰਾਵਾਂ ਵੀ ਹਨ, ਜੋ ਕਿ ਨਾਮ ਤੋਂ ਹੀ ਪਤਾ ਲੱਗਦਾ ਹੈ, ਚੁੰਬਕਤਾ ਦੀ ਵਿਆਖਿਆ ਕਰਨ ਲਈ ਵੀ ਪੇਸ਼ ਕੀਤੀਆਂ ਗਈਆਂ ਹਨ। ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿਚ, ਉਹ ਮੌਜੂਦਾ “ਚਾਰਜ ਅੰਦੋਲਨ” ਦੇ ਮੂਲ ਗੁਣ ਤੋਂ ਟੁੱਟ ਚੁੱਕੇ ਹਨ!

ਇਹ ਹੈਰਾਨੀਜਨਕ ਹੈ! ਕੋਈ ਇਲੈਕਟ੍ਰਿਕ ਚਾਰਜ ਗਤੀ ਨਹੀਂ ਹੈ, ਇਸ ਲਈ ਇਸਨੂੰ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਕਿਉਂ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ?

ਚਿੰਤਾ ਨਾ ਕਰੋ, ਅਤੇ ਹੌਲੀ ਹੌਲੀ ਮੇਰੀ ਗੱਲ ਸੁਣੋ।

ਆਉ ਪਹਿਲਾਂ ਚੁੰਬਕੀ ਕਰੰਟ ਨੂੰ ਵੇਖੀਏ।

ਇਹ ਪਾਇਆ ਗਿਆ ਕਿ ਚੁੰਬਕਤਾ ਬਿਜਲੀ ਦੀ ਗਤੀ ਦੇ ਕਾਰਨ ਹੁੰਦੀ ਹੈ (ਫਿਲਹਾਲ ਸਪਿੱਨ ਦੇ ਅੰਦਰੂਨੀ ਗੁਣਾਂ ਦੁਆਰਾ ਚੁੰਬਕਤਾ ਦੀ ਵਿਆਖਿਆ ‘ਤੇ ਵਿਚਾਰ ਨਹੀਂ ਕਰਨਾ)। ਕੁਦਰਤੀ ਚੁੰਬਕਤਾ ਦੀ ਵਿਆਖਿਆ ਕਰਨ ਲਈ, ਫਰਾਂਸੀਸੀ ਭੌਤਿਕ ਵਿਗਿਆਨੀ ਐਂਪੀਅਰ ਨੇ “ਮੌਲੀਕਿਊਲਰ ਸਰਕੂਲੇਸ਼ਨ” ਦੀ ਪਰਿਕਲਪਨਾ ਨੂੰ ਅੱਗੇ ਰੱਖਿਆ।

ਜਿਵੇਂ ਕਿ ਹੇਠਾਂ ਦਿੱਤੀ ਗਈ ਤਸਵੀਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ, ਕਿਸੇ ਵੀ ਪਰਮਾਣੂ ਜਾਂ ਅਣੂ ਨੂੰ ਕੇਂਦਰ ਦੇ ਦੁਆਲੇ ਘੁੰਮਦੇ ਹੋਏ ਇੱਕ ਇਲੈਕਟ੍ਰਿਕ ਚਾਰਜ ਦੇ ਰੂਪ ਵਿੱਚ ਮੰਨਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਇੱਕ ਛੋਟਾ ਜਿਹਾ ਲੂਪ ਕਰੰਟ ਬਣਾਉਂਦਾ ਹੈ, ਯਾਨੀ “ਮੌਲੀਕਿਊਲਰ ਸਰਕੂਲੇਸ਼ਨ”।

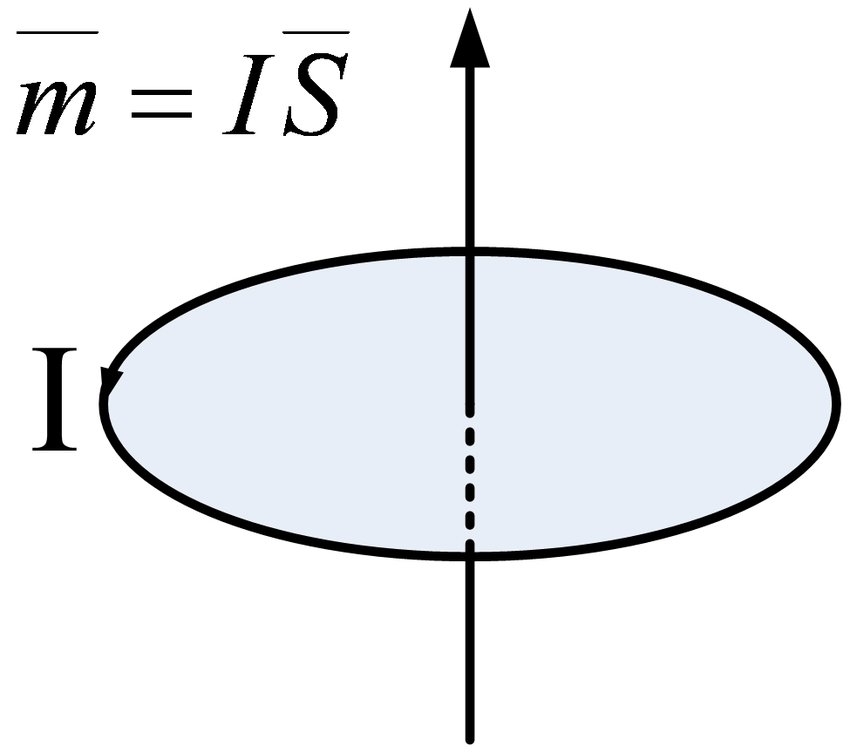
ਕਾਨੂੰਨ ਦੇ ਅਨੁਸਾਰ ਕਿ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਚੁੰਬਕੀ ਖੇਤਰ ਨੂੰ ਉਤੇਜਿਤ ਕਰਦਾ ਹੈ, ਇਹ ਅਣੂ ਸਰਕੂਲੇਸ਼ਨ ਇੱਕ ਭੌਤਿਕ ਮਾਤਰਾ ਪੈਦਾ ਕਰੇਗਾ ਜਿਸਨੂੰ ਚੁੰਬਕੀ ਮੋਮੈਂਟ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇਸਦਾ ਆਕਾਰ ਅਣੂ ਸਰਕੂਲੇਸ਼ਨ ਦੇ ਬਰਾਬਰ ਵਰਤਮਾਨ ਦੁਆਰਾ ਗੁਣਾ ਕੀਤੇ ਅਣੂ ਸਰਕੂਲੇਸ਼ਨ ਦੁਆਰਾ ਘਿਰਿਆ ਹੋਇਆ ਖੇਤਰ ਹੈ, ਅਤੇ ਇਸਦੀ ਦਿਸ਼ਾ ਸਰਕੂਲੇਸ਼ਨ ਦੀ ਦਿਸ਼ਾ ਦੇ ਨਾਲ ਇੱਕ ਸੱਜੇ-ਹੱਥ ਸਪਿਰਲ ਸਬੰਧ ਵਿੱਚ ਹੈ, ਅਰਥਾਤ

ਸਪੱਸ਼ਟ ਤੌਰ ‘ਤੇ, ਚੁੰਬਕੀ ਪਲ ਦੀ ਦਿਸ਼ਾ ਸਰਕੂਲੇਟ ਕਰੰਟ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਚੁੰਬਕੀ ਖੇਤਰ ਦੀ ਦਿਸ਼ਾ ਦੇ ਬਿਲਕੁਲ ਨਾਲ ਹੈ

.

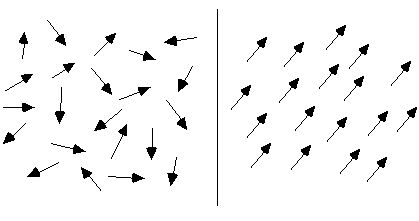
ਆਮ ਹਾਲਤਾਂ ਵਿੱਚ, ਕਿਸੇ ਪਦਾਰਥ ਦੇ ਅਣੂ ਦੇ ਗੇੜ ਦੀ ਵਿਵਸਥਾ ਅਰਾਜਕ ਹੁੰਦੀ ਹੈ, ਇਸਲਈ ਪਦਾਰਥ ਚੁੰਬਕੀ ਨਹੀਂ ਹੁੰਦਾ, ਜਿਵੇਂ ਕਿ ਹੇਠਾਂ ਚਿੱਤਰ ਦੇ ਖੱਬੇ ਪਾਸੇ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਜਦੋਂ ਇੱਕ ਬਾਹਰੀ ਚੁੰਬਕੀ ਖੇਤਰ ਦੇ ਅਧੀਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਹ ਅਣੂ ਸਰਕੂਲੇਸ਼ਨ ਲਗਭਗ ਸੁਚੱਜੇ ਢੰਗ ਨਾਲ ਵਿਵਸਥਿਤ ਕੀਤੇ ਜਾਣਗੇ। ਜਿਵੇਂ ਕਿ ਹੇਠਾਂ ਚਿੱਤਰ ਦੇ ਸੱਜੇ ਪਾਸੇ ਦਿਖਾਇਆ ਗਿਆ ਹੈ, ਉਹਨਾਂ ਦੇ ਚੁੰਬਕੀ ਪਲਾਂ ਨੂੰ ਜਿੰਨਾ ਸੰਭਵ ਹੋ ਸਕੇ ਇੱਕ ਦਿਸ਼ਾ ਵਿੱਚ ਵਿਵਸਥਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ ਅਣਗਿਣਤ ਛੋਟੀਆਂ ਚੁੰਬਕੀ ਸੂਈਆਂ ਇੱਕ ਕੁੱਲ ਚੁੰਬਕੀ ਖੇਤਰ ਬਣਾਉਣ ਲਈ ਇਕੱਠੀਆਂ ਹੁੰਦੀਆਂ ਹਨ, ਅਤੇ ਉਹਨਾਂ ਤੋਂ ਬਣੀ ਸਾਰੀ ਸਮੱਗਰੀ ਚੁੰਬਕੀ ਬਣ ਜਾਂਦੀ ਹੈ।

ਮੰਨ ਲਓ ਕਿ ਇੱਕ ਬੇਲਨਾਕਾਰ ਚੁੰਬਕ ਹੈ, ਅੰਦਰਲੇ ਅਣੂ ਸਰਕੂਲੇਸ਼ਨ ਨੂੰ ਚੰਗੀ ਤਰ੍ਹਾਂ ਵਿਵਸਥਿਤ ਕੀਤਾ ਗਿਆ ਹੈ, ਅਤੇ ਚੁੰਬਕ ਸੈਕਸ਼ਨ ਦੇ ਕਿਨਾਰੇ ‘ਤੇ ਹਰੇਕ ਅਣੂ ਦੇ ਸਰਕੂਲੇਸ਼ਨ ਦੇ ਭਾਗ ਇੱਕ ਵਿਸ਼ਾਲ ਸਰਕੂਲੇਸ਼ਨ ਬਣਾਉਣ ਲਈ ਇੱਕ ਦੂਜੇ ਨਾਲ ਜੁੜੇ ਹੋਏ ਹਨ, ਜਿਵੇਂ ਕਿ ਹੇਠਾਂ ਦਿੱਤੇ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ।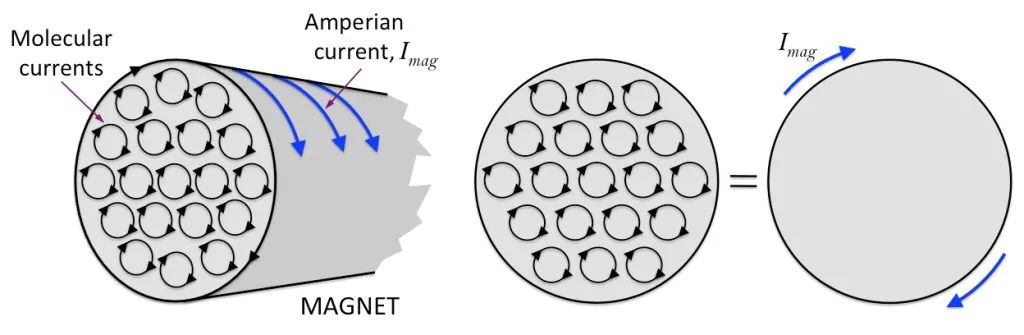

ਇਸਦੇ ਅਧਾਰ ਤੇ, ਅਸੀਂ ਸੋਚ ਸਕਦੇ ਹਾਂ ਕਿ ਇੱਕ ਬਾਰ ਮੈਗਨੇਟ ਇੱਕ ਊਰਜਾਵਾਨ ਸੋਲਨੋਇਡ ਵਰਗਾ ਹੈ। ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਚੁੰਬਕ ਦੀ ਸਤ੍ਹਾ ਉੱਤੇ ਇੱਕ ਅਦਿੱਖ ਕਰੰਟ ਉਲਝਿਆ ਹੋਇਆ ਹੈ! ਇਸ ਕਿਸਮ ਦਾ ਕਰੰਟ ਜੁੜਿਆ ਅਤੇ ਵਰਤਿਆ ਨਹੀਂ ਜਾ ਸਕਦਾ। ਇਹ ਚੁੰਬਕ ਦੀ ਸਤ੍ਹਾ ਤੱਕ ਸੀਮਤ ਹੈ। ਅਸੀਂ ਇਸਨੂੰ “ਬਾਈਡਿੰਗ ਕਰੰਟ” ਜਾਂ “ਮੈਗਨੈਟਾਈਜ਼ਿੰਗ ਕਰੰਟ” ਕਹਿੰਦੇ ਹਾਂ।

ਇਸ ਲਈ, ਚੁੰਬਕੀ ਕਰੰਟ ਇੱਕ ਕਰੰਟ ਹੈ, ਕਿਉਂਕਿ ਇਹ ਅਸਲ ਇਲੈਕਟ੍ਰਿਕ ਚਾਰਜ ਦੀ ਗਤੀ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਕਰੰਟ ਦੇ ਸਮਾਨ ਹੈ, ਜੋ ਬਰਾਬਰ ਇੱਕ ਚੁੰਬਕੀ ਖੇਤਰ ਪੈਦਾ ਕਰ ਸਕਦਾ ਹੈ!

ਆਉ ਮੁੜ ਵਿਸਥਾਪਨ ਕਰੰਟ ਨੂੰ ਵੇਖੀਏ।

ਐਂਪੀਅਰ ਦੇ ਲੂਪ ਪ੍ਰਮੇਏ ਦੇ ਅਨੁਸਾਰ, ਇੱਕ ਬੰਦ ਮਾਰਗ ‘ਤੇ ਚੁੰਬਕੀ ਖੇਤਰ ਦੀ ਤਾਕਤ ਦਾ ਅਟੁੱਟ ਹੋਣਾ ਇਸ ਮਾਰਗ ਦੁਆਰਾ ਬੰਨ੍ਹੀ ਹੋਈ ਕਿਸੇ ਵੀ ਵਕਰ ਸਤਹ ‘ਤੇ ਮੌਜੂਦਾ ਘਣਤਾ ਦੇ ਪ੍ਰਵਾਹ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ, ਯਾਨੀ ਇਸ ਥਿਊਰਮ ਨੂੰ ਗਣਿਤ ਵਿੱਚ ਸਟੋਕਸ ਦੀ ਥਿਊਰਮ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਇਹ ਸਾਨੂੰ ਦੱਸਦਾ ਹੈ ਕਿ ਕਿਸੇ ਵੀ ਬੰਦ ਮਾਰਗ ਦੇ ਨਾਲ ਇੱਕ ਵੈਕਟਰ ਦਾ ਇੰਟੈਗਰਲ ਬੰਦ ਮਾਰਗ ਦੁਆਰਾ ਬੰਨ੍ਹੀ ਕਿਸੇ ਵੀ ਸਤਹ ਤੱਕ ਇਸਦੇ ਕਰਲ (ਇੱਥੇ) ਦੇ ਪ੍ਰਵਾਹ ਦੇ ਬਰਾਬਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ।

ਕਿਉਂਕਿ ਇਹ ਇੱਕ ਗਣਿਤਿਕ ਪ੍ਰਮੇਯ ਹੈ, ਇਸ ਲਈ ਇਹ ਹਮੇਸ਼ਾ ਸਹੀ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ, ਕਿਉਂਕਿ ਗਣਿਤ ਇੱਕ ਤਾਰਕਿਕ ਪ੍ਰਣਾਲੀ ਹੈ, ਜੋ ਸਵੈ-ਸਿੱਧਾਂ ‘ਤੇ ਅਧਾਰਤ ਹੈ।

ਇਸ ਲਈ, ਐਂਪੀਅਰ ਲੂਪ ਥਿਊਰਮ ਨੂੰ ਹਮੇਸ਼ਾ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ!

ਹਾਲਾਂਕਿ, ਪ੍ਰਤਿਭਾਸ਼ਾਲੀ ਸਕਾਟਿਸ਼ ਭੌਤਿਕ ਵਿਗਿਆਨੀ ਮੈਕਸਵੈੱਲ ਨੇ ਖੋਜ ਕੀਤੀ ਕਿ ਜਦੋਂ ਇੱਕ ਅਸਥਿਰ ਕਰੰਟ ਸਰਕਟ ਦਾ ਸਾਹਮਣਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਐਂਪੀਅਰ ਲੂਪ ਥਿਊਰਮ ਵਿਰੋਧੀ ਸੀ।

ਆਮ ਅਸਥਿਰ ਕਰੰਟ ਕੈਪੇਸੀਟਰ ਦੇ ਚਾਰਜਿੰਗ ਅਤੇ ਡਿਸਚਾਰਜ ਦੇ ਦੌਰਾਨ ਹੁੰਦਾ ਹੈ। ਜਿਵੇਂ ਕਿ ਹੇਠਾਂ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ, ਕੈਪੀਸੀਟਰ ਚਾਰਜਿੰਗ ਦੀ ਛੋਟੀ ਮਿਆਦ ਦੇ ਦੌਰਾਨ ਇੱਕ ਅਸਥਿਰ ਕਰੰਟ ਹੁੰਦਾ ਹੈ।

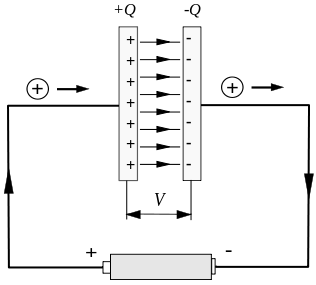
ਪਰ ਸਰਕਟ ਕੈਪੇਸੀਟਰ ਪਲੇਟਾਂ ਦੇ ਵਿਚਕਾਰ ਡਿਸਕਨੈਕਟ ਹੋ ਗਿਆ ਹੈ, ਜਿਸ ਨਾਲ ਇੱਕ ਗੰਭੀਰ ਸਮੱਸਿਆ ਪੈਦਾ ਹੋਵੇਗੀ।

ਮੰਨ ਲਓ ਕਿ ਅਸੀਂ ਇੱਕ ਬੰਦ ਮਾਰਗ ‘ਤੇ ਵਿਚਾਰ ਕਰਦੇ ਹਾਂ ਜੋ ਤਾਰ ਨੂੰ ਬਾਈਪਾਸ ਕਰਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ ਹੇਠਾਂ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ, C ਦੁਆਰਾ ਚਿੰਨ੍ਹਿਤ ਚੱਕਰ, ਅਤੇ ਇਸਦੇ ਨਾਲ ਵਕਰ ਸਤਹ ਨੂੰ ਸੀਮਾ ਵਜੋਂ ਚੁਣਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਚਿੱਤਰ ਵਿੱਚ, C ਦੁਆਰਾ ਘਿਰਿਆ ਗੋਲਾਕਾਰ ਪਲੇਨ ਅਤੇ ਕੈਪੇਸੀਟਰ ਦੇ ਪਾਰ ਚੁਣਿਆ ਗਿਆ ਹੈ। ਖੱਬੀ ਪਲੇਟ ਦੀ ਕਰਵ ਸਤਹ।

ਗੋਲਾਕਾਰ ਸਤਹ ਦੇ ਅਨੁਸਾਰ, ਇਹ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਵਕਰ ਸਤਹ ਦੇ ਅਨੁਸਾਰ, ਪਰ ਚੁੰਬਕੀ ਖੇਤਰ ਦੀ ਤਾਕਤ ਦੇ ਇੱਕ ਲੂਪ ਅਟੁੱਟ ਦੇ ਰੂਪ ਵਿੱਚ, ਇਸਦਾ ਮੁੱਲ ਨਿਰਧਾਰਤ ਕੀਤਾ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ!

ਕਿਵੇਂ ਕਰੀਏ?

ਮੈਕਸਵੈੱਲ ਦਾ ਮੰਨਣਾ ਹੈ ਕਿ ਐਂਪੀਅਰ ਦਾ ਲੂਪ ਥਿਊਰਮ ਸਥਾਪਿਤ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ। ਹੁਣ ਜਦੋਂ ਕੋਈ ਸਮੱਸਿਆ ਹੈ, ਇਹ ਇਸ ਲਈ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿਉਂਕਿ ਵਰਤਮਾਨ ਦਾ ਇੱਕ ਹਿੱਸਾ ਸਾਡੇ ਦੁਆਰਾ ਪਹਿਲਾਂ ਨਹੀਂ ਖੋਜਿਆ ਗਿਆ ਸੀ, ਪਰ ਇਹ ਮੌਜੂਦ ਹੈ!

ਇਸ ਲਈ, ਵਰਤਮਾਨ ਦੇ ਇਸ ਹਿੱਸੇ ਦਾ ਪਤਾ ਕਿਵੇਂ ਲਗਾਇਆ ਜਾਵੇ?

ਕਿਉਂਕਿ ਸਮੱਸਿਆ ਪਲੇਟਾਂ ਦੇ ਵਿਚਕਾਰ ਹੈ, ਪਲੇਟਾਂ ਦੇ ਵਿਚਕਾਰ ਤੋਂ ਸ਼ੁਰੂ ਕਰੋ।

ਵਿਸ਼ਲੇਸ਼ਣ ਦੁਆਰਾ, ਮੈਕਸਵੈੱਲ ਨੇ ਪਾਇਆ ਕਿ ਚਾਰਜਿੰਗ ਜਾਂ ਡਿਸਚਾਰਜਿੰਗ ਦੀ ਪਰਵਾਹ ਕੀਤੇ ਬਿਨਾਂ, ਕੈਪੀਸੀਟਰ ਪਲੇਟਾਂ ਦੇ ਵਿਚਕਾਰ ਹਰ ਸਮੇਂ ਇੱਕ ਭੌਤਿਕ ਮਾਤਰਾ ਹੁੰਦੀ ਹੈ ਜੋ ਕਰੰਟ ਦੀ ਤੀਬਰਤਾ ਅਤੇ ਦਿਸ਼ਾ ਨਾਲ ਸਮਕਾਲੀ ਹੁੰਦੀ ਹੈ। ਇਹ ਇਲੈਕਟ੍ਰਿਕ ਡਿਸਪਲੇਸਮੈਂਟ ਵੈਕਟਰ ਦੇ ਪ੍ਰਵਾਹ ਦਾ ਸਮਾਂ ਡੈਰੀਵੇਟਿਵ ਹੈ, ਯਾਨੀ ਇਸਨੂੰ ਵਿਸਥਾਪਨ ਕਰੰਟ ਵਜੋਂ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਗਿਆ ਹੈ।

ਜੇ ਇਹ ਮੰਨਿਆ ਜਾਵੇ ਕਿ ਇਹ ਹਿੱਸਾ ਕਰੰਟ ਦਾ ਉਹ ਹਿੱਸਾ ਹੈ ਜੋ ਪਹਿਲਾਂ ਨਹੀਂ ਖੋਜਿਆ ਗਿਆ ਸੀ, ਤਾਂ ਹੁਣ ਪੂਰਾ ਕਰੰਟ ਹੈ। ਕਹਿਣ ਦਾ ਭਾਵ ਹੈ, ਹਾਲਾਂਕਿ ਪਲੇਟਾਂ ਦੇ ਵਿਚਕਾਰ ਸਰਕਟ ਡਿਸਕਨੈਕਟ ਹੋ ਗਿਆ ਹੈ, ਇਲੈਕਟ੍ਰਿਕ ਡਿਸਪਲੇਸਮੈਂਟ ਫਲੈਕਸ ਦਾ ਡੈਰੀਵੇਟਿਵ ਅਤੇ ਕਰੰਟ ਦਾ ਜੋੜ, ਸਮੁੱਚੇ ਤੌਰ ‘ਤੇ, ਹਰ ਸਮੇਂ ਕਰੰਟ ਦੀ ਨਿਰੰਤਰਤਾ ਨੂੰ ਯਕੀਨੀ ਬਣਾਉਂਦਾ ਹੈ।

ਪਿਛਲੇ ਵਿਰੋਧਾਭਾਸ ਵੱਲ ਮੁੜਦੇ ਹੋਏ, ਅਸੀਂ ਹੁਣ ਜਾਣਦੇ ਹਾਂ ਕਿ, ਸਟੋਕਸ ਦੇ ਸਿਧਾਂਤ ਦੀਆਂ ਲੋੜਾਂ ਦੇ ਅਨੁਸਾਰ, ਬੰਦ ਸਤਹ ਲਈ ਮੌਜੂਦਾ ਘਣਤਾ ਦੇ ਵਹਾਅ ਦੀ ਗਣਨਾ ਕਰਦੇ ਸਮੇਂ, ਵਿਸਥਾਪਨ ਕਰੰਟ ਦੀ ਘਣਤਾ ਨੂੰ ਵੀ ਮੰਨਿਆ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ, ਯਾਨੀ ਸੰਪੂਰਨ ਐਂਪੀਅਰ ਲੂਪ। ਇਸ ਲਈ ਪ੍ਰਮੇਯ ਹੈ, ਇਸ ਨਵੇਂ ਮੌਜੂਦਾ ਹਿੱਸੇ ਨੂੰ “ਖੋਜ” ਕੇ, ਐਂਪੀਅਰ ਲੂਪ ਥਿਊਰਮ ਦਾ ਸੰਕਟ ਹੱਲ ਹੋ ਗਿਆ ਹੈ!

ਕਾਰਨ ਇੱਥੇ “ਜਾਣ-ਪਛਾਣ” ਦੀ ਵਰਤੋਂ ਨਹੀਂ ਕੀਤੀ ਗਈ ਹੈ, ਪਰ ਇੱਥੇ “ਖੋਜ” ਵਰਤੀ ਗਈ ਹੈ। ਜੋ ਮੈਂ ਜ਼ੋਰ ਦੇਣਾ ਚਾਹੁੰਦਾ ਹਾਂ ਉਹ ਇਹ ਹੈ ਕਿ ਇਸ ਕਿਸਮ ਦਾ ਵਰਤਮਾਨ ਇੱਕ ਗਣਿਤਿਕ ਮੁਆਵਜ਼ਾ ਨਹੀਂ ਹੈ, ਪਰ ਇੱਕ ਅਸਲੀ ਚੀਜ਼ ਹੈ, ਪਰ ਇਹ ਪਹਿਲਾਂ ਖੋਜਿਆ ਨਹੀਂ ਗਿਆ ਹੈ.

ਇਹ ਪਹਿਲੀ ਥਾਂ ‘ਤੇ ਕਿਉਂ ਮੌਜੂਦ ਹੈ? ਕਿਉਂਕਿ ਇਹ ਇੱਕ ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਦੇ ਤੌਰ ਤੇ ਕੰਮ ਕਰਦਾ ਹੈ, ਇੱਕ ਸੰਚਾਲਨ ਕਰੰਟ ਵਾਂਗ, ਇਹ ਇੱਕ ਚੁੰਬਕੀ ਖੇਤਰ ਨੂੰ ਬਰਾਬਰ ਉਤੇਜਿਤ ਕਰਦਾ ਹੈ, ਸਿਵਾਏ ਇਸ ਤੋਂ ਇਲਾਵਾ ਕਿ ਬਿਜਲੀ ਦੇ ਚਾਰਜ ਦੀ ਕੋਈ ਗਤੀ ਨਹੀਂ ਹੈ, ਕੋਈ ਤਾਰ ਦੀ ਲੋੜ ਨਹੀਂ ਹੈ, ਅਤੇ ਕੋਈ ਜੂਲ ਤਾਪ ਪੈਦਾ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਇਸਲਈ ਇਸਨੂੰ ਅਣਡਿੱਠ ਕੀਤਾ ਗਿਆ ਹੈ!

ਪਰ ਇਹ ਅਸਲ ਵਿੱਚ ਆਪਣੇ ਆਪ ਹੀ ਮੌਜੂਦ ਹੈ, ਸਿਰਫ ਇੱਕ ਘੱਟ ਪ੍ਰੋਫਾਈਲ ਰੱਖੋ, ਇਹ ਚੁੱਪਚਾਪ ਚੁੰਬਕੀ ਖੇਤਰ ਨੂੰ ਹਰ ਸਮੇਂ ਉਤੇਜਿਤ ਕਰਦਾ ਰਿਹਾ ਹੈ!

ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਜਦੋਂ ਅਸੀਂ ਇੱਕ ਚੁੰਬਕੀ ਖੇਤਰ ਦਾ ਸਾਹਮਣਾ ਕਰਦੇ ਹਾਂ, ਤਾਂ ਕਰੰਟ ਦੀ ਅਸਲ ਪਰਿਭਾਸ਼ਾ ਬਹੁਤ ਤੰਗ ਹੁੰਦੀ ਹੈ। ਇਲੈਕਟ੍ਰਿਕ ਕਰੰਟ ਦਾ ਤੱਤ ਇਲੈਕਟ੍ਰਿਕ ਚਾਰਜ ਦੀ ਗਤੀ ਨਹੀਂ ਹੈ, ਇਹ ਅਜਿਹੀ ਚੀਜ਼ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਜੋ ਚੁੰਬਕੀ ਖੇਤਰ ਨੂੰ ਉਤੇਜਿਤ ਕਰ ਸਕਦੀ ਹੈ।

ਹੁਣ ਤੱਕ, ਵਰਤਮਾਨ ਦੇ ਕਈ ਰੂਪ ਪੇਸ਼ ਕੀਤੇ ਗਏ ਹਨ. ਉਹ ਸਾਰੇ ਬਾਹਰਮੁਖੀ ਤੌਰ ‘ਤੇ ਮੌਜੂਦ ਹਨ, ਅਤੇ ਜੋ ਉਹਨਾਂ ਵਿੱਚ ਸਾਂਝਾ ਹੈ ਉਹ ਇਹ ਹੈ ਕਿ ਸਾਰੀਆਂ ਕਰੰਟਾਂ ਚੁੰਬਕੀ ਖੇਤਰ ਨੂੰ ਬਰਾਬਰ ਉਤੇਜਿਤ ਕਰ ਸਕਦੀਆਂ ਹਨ।