برقی رو کیا ہے؟ پہلے یاد کریں، کرنٹ کی تعریف کیا ہے جو ہم نے سیکھی ہے؟

بالکل آسان، ایک موصل میں چارج شدہ ذرات کی دشاتمک حرکت ایک برقی رو ہے۔

Only when a substance has charged particles that can move freely, it can transmit electric current—that is, conduct electricity. These charged particles that participate in conduction are called carriers. For metals, for example, only the outer electrons of atoms can act as carriers.

The “directional movement” in the definition of electric current is often misunderstood. Many people think it refers to movement with a certain direction, of course not! Doesn’t the direction of movement of the electrons in the AC circuit change?

درحقیقت، اورینٹیئرنگ “بے ترتیب حرکت” سے متعلق ہے!

Since electrons are microscopic particles, they must be in thermal motion all the time. Thermal motion is a random motion, as shown in the figure below.

یہ تحریک دراصل بہت تیز ہے۔ مثال کے طور پر، کمرے کے درجہ حرارت پر دھاتوں میں، الیکٹرانک تھرمل حرکت کی رفتار سینکڑوں کلومیٹر فی سیکنڈ کی ترتیب پر ہوتی ہے!

اگر آپ اس بے ترتیب حرکت کو قریب سے دیکھیں تو آپ دیکھیں گے کہ ہر ذرے کی حرکت کی سمت کسی بھی لمحے بے ترتیب ہے۔ اگر آپ ان ذرات کی رفتار ویکٹر کو جوڑتے ہیں تو نتیجہ تقریباً صفر ہوتا ہے۔

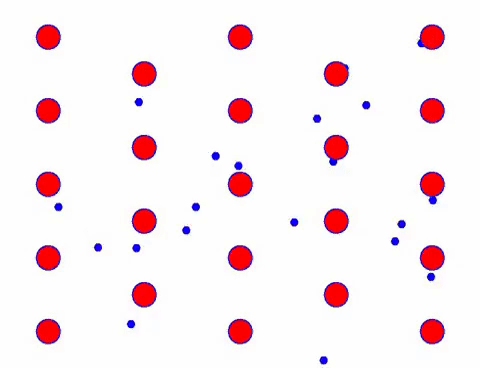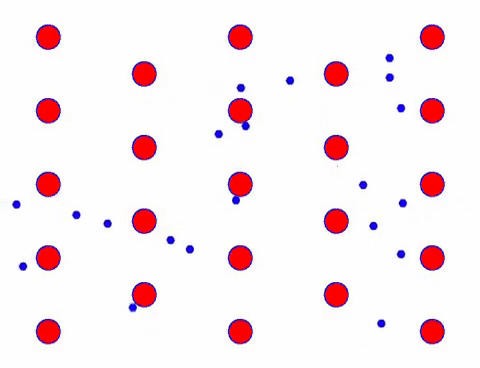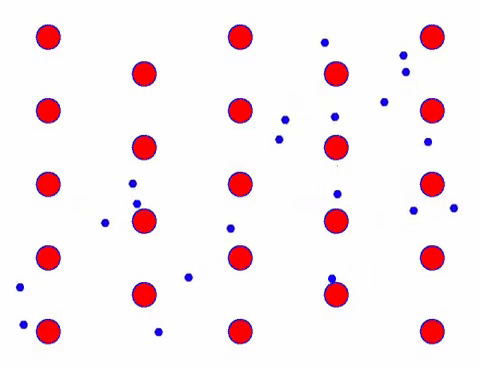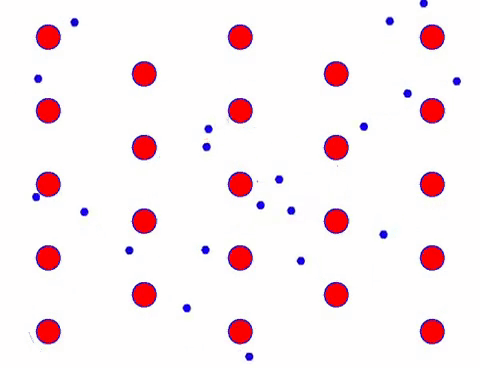
اب کنڈکٹر میں ایک برقی فیلڈ شامل کریں، اور الیکٹران بے ترتیب حرکت کی بنیاد پر ایک دشاتمک حرکت کو سپرد کرتا ہے۔ یہ فرض کرتے ہوئے کہ برقی میدان ایک مخصوص مدت کے لیے بائیں جانب ہے، الیکٹران کی حرکت مندرجہ ذیل کی طرح نظر آتی ہے۔ سرخ گیندیں کرسٹل جالی پر دھاتی ایٹموں کی نمائندگی کرتی ہیں، اور تیزی سے حرکت کرنے والے نقطے آزاد الیکٹران کی نمائندگی کرتے ہیں۔

کیا یہ تیز نظر آتا ہے؟ اس کی وجہ یہ ہے کہ الیکٹرانک تحریک واقعی تیز ہے! لیکن درحقیقت، بے ترتیب حرکت، جو اس کا ایک بڑا حصہ ہے، کرنٹ میں حصہ نہیں ڈالتی۔ جب بے ترتیب حرکت کو ختم کر دیا جاتا ہے، تو باقی بالکل نیچے کی سست نظر کی طرح ہوتا ہے۔

Indeed, the directional movement of electrons is much slower than the speed of thermal movement. This “grinding” movement of electrons is called drift, or “drift”. Sometimes, electrons will run in the opposite direction because of collisions with atoms. But in general, electrons move in one direction.

اگر برقی میدان کی سمت بدل جائے تو الیکٹران کے بڑھنے کی سمت بھی بدل جائے گی۔

لہذا، اس قسم کی سمتی حرکت کا مطلب یہ ہے کہ ایک خاص وقت میں ترسیل میں حصہ لینے والے تمام الیکٹرانوں کی رفتار کا مجموعہ صفر نہیں ہے، لیکن عام طور پر ایک خاص سمت میں ہوتا ہے۔ اس سمت کو کسی بھی وقت تبدیل کیا جا سکتا ہے، اور یہ متبادل کرنٹ کا معاملہ ہے۔

لہٰذا، کرنٹ الیکٹرک چارج کی اتنی “دشاتمک حرکت” نہیں ہے جتنی کہ یہ برقی چارج کی “اجتماعی حرکت” ہے۔

موصل میں کرنٹ کی شدت موجودہ شدت سے ظاہر ہوتی ہے۔ موجودہ شدت کو یونٹ کے وقت میں کنڈکٹر کے کراس سیکشن سے گزرنے والی بجلی کی مقدار کے طور پر بیان کیا جاتا ہے، یعنی

ہم نے کچھ جسمانی مقداریں سیکھی ہیں جن میں لفظ “شدت” ہوتا ہے، جیسے الیکٹرک فیلڈ کی شدت اور مقناطیسی انڈکشن کی شدت۔ وہ عام طور پر فی یونٹ وقت، یونٹ کا رقبہ (یا یونٹ کا حجم، یونٹ ٹھوس زاویہ) کی تقسیم کی نمائندگی کرتے ہیں۔ تاہم، موجودہ شدت میں لفظ “شدت” علاقے کی موجودہ تقسیم کی عکاسی نہیں کرتا ہے۔

درحقیقت، ایک اور طبعی مقدار کرنٹ کی رقبے میں تقسیم کے لیے ذمہ دار ہے، جو کہ کرنٹ کثافت ہے۔

چونکہ برقی رو کا جوہر برقی چارج کی دشاتمک حرکت ہے، اس لیے کرنٹ کی شدت اور بڑھنے کی رفتار کے درمیان ایک خاص رشتہ ہونا چاہیے!

اس تعلق کو حاصل کرنے کے لیے، ہمیں سب سے پہلے تصور کیرئیر کی حراستی کو واضح کرنا ہوگا، یعنی، یونٹ والیوم میں کیریئرز کی تعداد، جس کا اظہار  سے ہوتا ہے۔

یہ فرض کیا جاتا ہے کہ کنڈکٹر کراس سیکشن ہے، کیریئر کا ارتکاز ہے، بڑھے ہوئے رفتار ہے، اور چارج شدہ چارج ہے۔

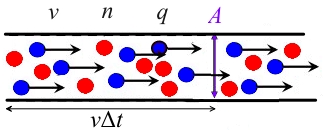
پھر سطح کے بائیں جانب موصل میں چارج ہوتا ہے، اور یہ چارجز ایک خاص مدت کے اندر سطح سے گزر جائیں گے، اس لیے

یہ موجودہ شدت کا خوردبینی اظہار ہے۔

موجودہ کثافت کرنٹ کی رقبہ میں تقسیم ہے، اس لیے کرنٹ کی کثافت کی شدت ہے، لیکن اس کی تعریف ایک ویکٹر کے طور پر کی جاتی ہے، اور سمت مثبت طور پر چارج کیے جانے والے کیریئرز کے بڑھے ہوئے رفتار ویکٹر کی سمت ہے، اس لیے الیکٹرانوں کا بہاؤ دھات اس رفتار سے حاصل کی جا سکتی ہے، ذیل میں ایک مثال کے طور پر۔

تانبے کے تار پر غور کریں، یہ فرض کرتے ہوئے کہ ہر تانبے کا ایٹم ایک برقی برقی بطور کیریئر کا حصہ ڈالتا ہے۔ تانبے کا 1 مول ہے، اس کا حجم ہے، داڑھ کا ماس ہے، کثافت ہے، پھر تانبے کے تار کا کیریئر کنسنٹریشن ہے

ایوگاڈرو کا مستقل کہاں ہے۔ تانبے کی کثافت پائی جاتی ہے، اور بدلنے سے حاصل ہونے والی قدر تقریباً یونٹ/کیوبک میٹر ہے۔

یہ فرض کرتے ہوئے کہ تانبے کے تار کا رداس 0.8 ملی میٹر ہے، کرنٹ کا بہاؤ 15A، = 1.6 C ہے، اور الیکٹرانوں کے بڑھنے کی رفتار کا حساب لگایا جاتا ہے۔

یہ دیکھا جا سکتا ہے کہ الیکٹران کے بڑھنے کی رفتار واقعی بہت چھوٹی ہے۔

سرکٹس کا مطالعہ کرنے والوں کے لیے اوپر کرنٹ کی مکمل تعریف ہے۔

لیکن طبیعیات میں، کرنٹ کی اوپر دی گئی تعریف دراصل صرف ایک تنگ تعریف ہے۔ زیادہ عام کرنٹ صرف کنڈکٹرز تک محدود نہیں ہیں، جب تک کہ برقی چارجز کی حرکت کرنٹ ہو۔ مثال کے طور پر، جب ہائیڈروجن ایٹم کے الیکٹران مرکزے کے گرد گھومتے ہیں، تو اس کے مدار میں ایک برقی رو پیدا ہوتا ہے۔

فرض کریں کہ الیکٹرانک چارج کی مقدار ہے اور حرکت کی مدت ہے۔ پھر جب بھی گزرتا ہے، لوپ کے کسی بھی کراس سیکشن سے چارج کی اتنی بڑی مقدار گزرتی ہے، لہذا موجودہ شدت مدت، تعدد اور کونیی رفتار کے درمیان تعلق پر مبنی ہے، اور کرنٹ کو اس طرح بھی ظاہر کیا جا سکتا ہے۔

For another example, a charged metal disk, rotating around its axis, also forms loop currents with different radii.

اس قسم کا کرنٹ ایک عام ترسیلی کرنٹ نہیں ہے اور جول حرارت پیدا نہیں کر سکتا! ایک حقیقی سرکٹ نہیں بنا سکتا۔

بصورت دیگر، کیا آپ مجھے اس بات کا حساب دیں گے کہ ہائیڈروجن ایٹم کے الیکٹران فی سیکنڈ میں کتنی جول حرارت پیدا کرتے ہیں؟

درحقیقت، ویکیوم میں کرنٹ اوہم کے قانون کو پورا نہیں کرتا۔ کیونکہ، ویکیوم میں چارج شدہ ذرات کی نقل و حرکت سے بننے والے برقی رو کے لیے، کیریئرز دھات میں موجود جالیوں کی طرح نہیں ٹکراتے ہیں، اس لیے ویکیوم میں کوئی مزاحمت اور کوئی کنڈکٹنس نہیں ہے۔

برقی چارجز کی حرکت برقی رو پیدا کرتی ہے، اور برقی چارج خود ہی برقی میدان کو متحرک کرتا ہے۔ اس سے غلط فہمی پیدا کرنا آسان ہے۔ اس لیے بہت سے لوگ سوچتے ہیں کہ چارج شدہ ذرات کی برقی میدان جو برقی رو کی تشکیل کرتی ہے، کو بے نقاب ہونا چاہیے۔ لیکن درحقیقت، عام کنڈکٹر میں کنڈکشن کرنٹ کے لیے، کیریئرز ایسے پس منظر پر بہتے ہیں جو مثبت چارج شدہ دھاتی آئنوں کی ایک بڑی تعداد پر مشتمل ہے، اور کنڈکٹر خود غیر جانبدار ہوتا ہے!

ہم اکثر اس قسم کے خصوصی کرنٹ کو “مساوی کرنٹ” کہتے ہیں۔ یہاں مساوی کا مطلب ہے کہ یہ ایک مقناطیسی میدان اسی بنیاد پر پیدا کرتا ہے جس طرح ایک عام ترسیلی کرنٹ!

یاد دہانی: یہاں “مساوی کرنٹ” کو سرکٹ تجزیہ میں “مساوی سرکٹ” کے ساتھ الجھائیں نہیں۔

درحقیقت، جب ہم نے پہلی بار مقناطیسی میدان کا مطالعہ کیا، تو بائیوٹ-سفار کے قانون میں برقی رو عامی برقی رو تھی جس میں یہ مساوی کرنٹ موجود تھا۔ بلاشبہ، میکسویل کی مساوات میں کنڈکشن کرنٹ بھی عام کرنٹ سے مراد ہے۔

جن لوگوں نے فوٹو الیکٹرک اثر کا مطالعہ کیا ہے وہ جانتے ہیں کہ جب فوٹو الیکٹران کیتھوڈ سے انوڈ کی طرف بڑھتا ہے، اگر ہوا کے اثر کو نظر انداز کر دیا جائے تو یہ کرنٹ ویکیوم میں برقی چارجز کی حرکت سے پیدا ہوتا ہے، اور کوئی مزاحمت نہیں ہوتی، اس لیے یہ اوہم کے قانون کی طرف سے محدود نہیں ہے.

تو، کیا طبیعیات میں برقی رو کے بارے میں صرف یہی بات ہے؟

نہیں! اس کی بھی دو اقسام ہیں، یعنی مقناطیسی کرنٹ اور ڈسپلیسمنٹ کرنٹ۔

یہ دو مساوی دھارے بھی ہیں، جو جیسا کہ نام سے ظاہر ہے، مقناطیسیت کی وضاحت کے لیے بھی متعارف کرایا گیا ہے۔ دوسرے لفظوں میں، وہ موجودہ “چارج موومنٹ” کی بنیادی خصوصیت سے الگ ہو چکے ہیں!

یہ حیرت انگیز ہے! کوئی برقی چارج حرکت نہیں ہے، تو اسے برقی رو کیوں کہا جا سکتا ہے؟

فکر مت کرو، اور میری بات آہستہ سے سنو۔

آئیے پہلے مقناطیسی کرنٹ کو دیکھیں۔

It was found that magnetism is caused by the movement of electricity (not considering the explanation of magnetism by the intrinsic properties of spin for the time being). In order to explain natural magnetism, French physicist Ampere put forward the hypothesis of “molecular circulation”.

جیسا کہ نیچے دی گئی تصویر میں دکھایا گیا ہے، کسی بھی ایٹم یا مالیکیول کو مرکز کے گرد گردش کرنے والے برقی چارج کے طور پر سمجھا جا سکتا ہے، جو ایک چھوٹا لوپ کرنٹ بناتا ہے، یعنی “سالماتی گردش”۔

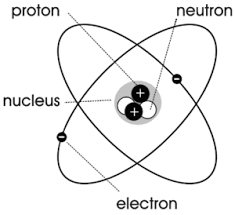
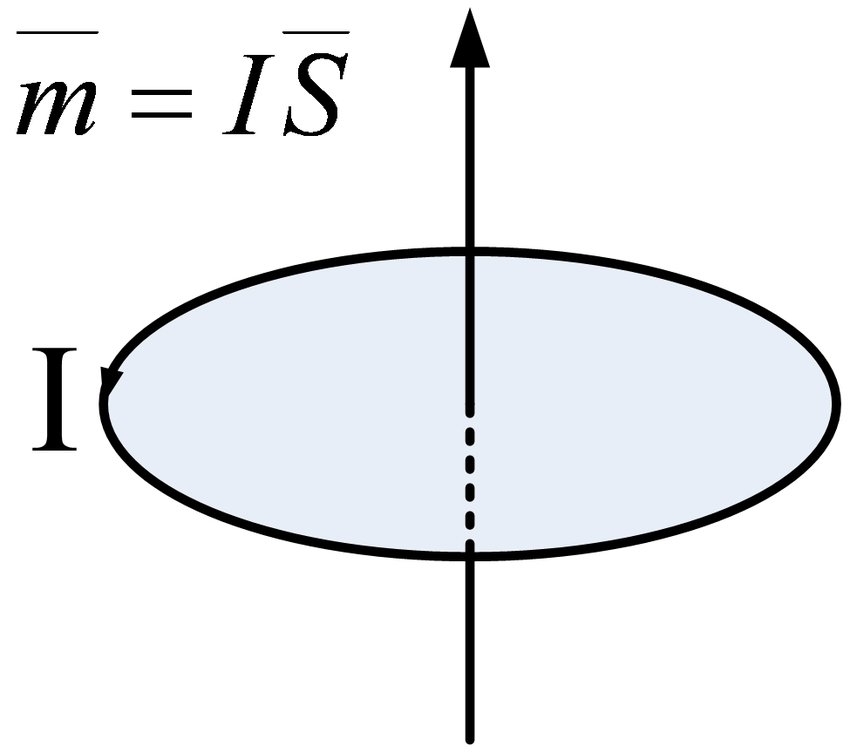
اس قانون کے مطابق کہ برقی رو مقناطیسی میدان کو اکساتی ہے، یہ سالماتی گردش ایک طبعی مقدار پیدا کرے گی جسے مقناطیسی لمحہ کہتے ہیں۔ اس کا سائز سالماتی گردش کے مساوی کرنٹ سے ضرب کردہ مالیکیولر گردش سے منسلک رقبہ ہے، اور اس کی سمت گردش کی سمت کے ساتھ دائیں ہاتھ کے سرپل تعلق میں ہے، یعنی

Obviously, the direction of the magnetic moment is exactly along the direction of the magnetic field formed by the circulating current

.

عام حالات میں، کسی مادہ کی سالماتی گردش کا انتظام انتشار کا شکار ہوتا ہے، اس لیے مادہ مقناطیسی نہیں ہوتا، جیسا کہ نیچے دی گئی تصویر کے بائیں جانب دکھایا گیا ہے۔ بیرونی مقناطیسی میدان کے تابع ہونے پر، یہ سالماتی گردشیں تقریباً صاف ستھرا ترتیب دی جائیں گی۔ جیسا کہ نیچے دیے گئے اعداد و شمار کے دائیں جانب دکھایا گیا ہے، ان کے مقناطیسی لمحات کو جتنا ممکن ہو ایک سمت میں ترتیب دیا جاتا ہے، بالکل اسی طرح جیسے لاتعداد چھوٹی مقناطیسی سوئیاں اکٹھی ہو کر ایک کل مقناطیسی میدان بناتی ہیں، اور ان پر مشتمل سارا مواد مقناطیسی بن جاتا ہے۔

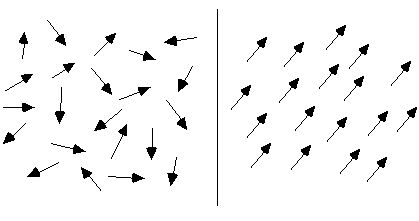
فرض کریں کہ ایک بیلناکار مقناطیس ہے، اندرونی سالماتی گردش کو صاف ستھرا ترتیب دیا گیا ہے، اور مقناطیس سیکشن کے کنارے پر ہر سالماتی گردش کے حصے ایک ساتھ جڑ کر ایک بڑی گردش تشکیل دیتے ہیں، جیسا کہ نیچے دی گئی تصویر میں دکھایا گیا ہے۔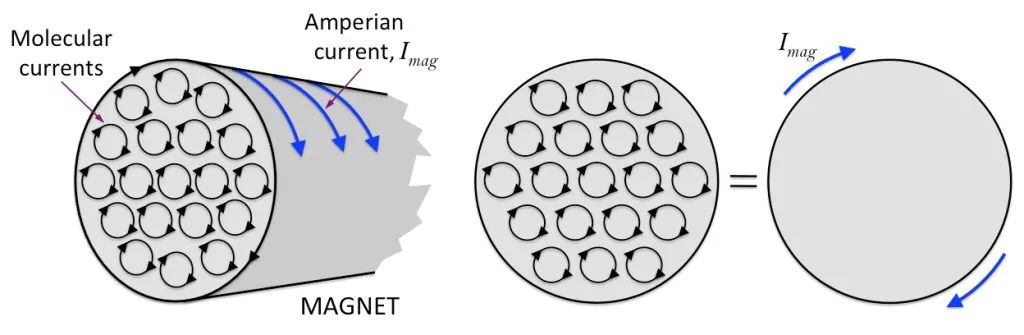

اس کی بنیاد پر، ہم سوچ سکتے ہیں کہ بار میگنیٹ ایک توانائی بخش سولینائڈ کی طرح ہے۔ دوسرے لفظوں میں، مقناطیس کی سطح پر ایک غیر مرئی کرنٹ الجھا ہوا ہے! اس قسم کا کرنٹ منسلک اور استعمال نہیں کیا جا سکتا۔ یہ مقناطیس کی سطح تک محدود ہے۔ ہم اسے “بائنڈنگ کرنٹ” یا “میگنیٹائزنگ کرنٹ” کہتے ہیں۔

لہذا، مقناطیسی کرنٹ ایک کرنٹ ہے، کیونکہ یہ اصلی برقی چارجز کی حرکت سے بننے والے کرنٹ کے برابر ہے، جو مساوی طور پر مقناطیسی میدان پیدا کر سکتا ہے!

آئیے دوبارہ نقل مکانی کرنٹ کو دیکھتے ہیں۔

ایمپیئر کے لوپ تھیوریم کے مطابق، بند راستے پر مقناطیسی میدان کی طاقت کا انضمام اس راستے سے منسلک کسی بھی خمیدہ سطح پر موجودہ کثافت کے بہاؤ کے برابر ہوتا ہے، یعنی اس تھیوریم کو ریاضی میں اسٹوکس تھیوریم کہا جاتا ہے۔ یہ ہمیں بتاتا ہے کہ کسی بھی بند راستے کے ساتھ ایک ویکٹر کا انضمام اس کے curl کے بہاؤ کے برابر ہونا چاہیے (یہاں) بند راستے سے جڑی کسی بھی سطح پر۔

Since it is a mathematical theorem, it must always be correct, because mathematics is a logical system based on axioms.

لہذا، ایمپیئر لوپ تھیوریم کو ہمیشہ رکھنا چاہیے!

تاہم، باصلاحیت سکاٹش ماہر طبیعیات میکسویل نے دریافت کیا کہ جب ایک غیر مستحکم کرنٹ کا سامنا کرنا پڑتا ہے، تو ایمپیئر لوپ تھیوریم متضاد تھا۔

عام غیر مستحکم کرنٹ کیپسیٹر کی چارجنگ اور ڈسچارج کے دوران ہوتا ہے۔ جیسا کہ نیچے دی گئی تصویر میں دکھایا گیا ہے، کیپسیٹر چارجنگ کی مختصر مدت کے دوران ایک غیر مستحکم کرنٹ ہوتا ہے۔

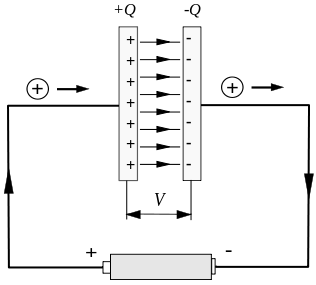
لیکن سرکٹ کپیسیٹر پلیٹوں کے درمیان منقطع ہے، جو ایک سنگین مسئلہ کا سبب بنے گا۔

فرض کریں کہ ہم ایک بند راستے پر غور کرتے ہیں جو تار کو نظرانداز کرتا ہے، جیسا کہ نیچے دی گئی تصویر میں دکھایا گیا ہے، C سے نشان زد دائرے اور اس کے ساتھ مڑے ہوئے سطح کو باؤنڈری کے طور پر منتخب کیا جا سکتا ہے۔ شکل میں، C خود اور کپیسیٹر کے اس پار بند سرکلر ہوائی جہاز کو منتخب کیا گیا ہے۔ بائیں پلیٹ کی خمیدہ سطح۔

سرکلر سطح کے مطابق، یہ دیکھا جا سکتا ہے کہ خمیدہ سطح کے مطابق، لیکن مقناطیسی میدان کی طاقت کے لوپ انٹیگرل کے طور پر، اس کی قدر کا تعین کیا جانا چاہیے!

کس طرح کرنا ہے؟

میکسویل کا خیال ہے کہ ایمپیئر کا لوپ تھیوریم قائم ہونا چاہیے۔ اب جب کہ ایک مسئلہ ہے، یہ اس لیے ہونا چاہیے کہ کرنٹ کا کوئی حصہ ہم نے پہلے دریافت نہیں کیا، لیکن یہ موجود ہے!

تو، موجودہ کے اس حصے کو کیسے تلاش کریں؟

چونکہ مسئلہ پلیٹوں کے درمیان ہے، پلیٹوں کے درمیان سے شروع کریں۔

تجزیہ کے ذریعے، میکسویل نے پایا کہ چارجنگ یا خارج ہونے سے قطع نظر، کپیسیٹر پلیٹوں کے درمیان ہر وقت ایک فزیکل مقدار ہوتی ہے جو کرنٹ کی شدت اور سمت کے ساتھ ہم آہنگ ہوتی ہے۔ یہ برقی نقل مکانی ویکٹر کے بہاؤ کا وقت مشتق ہے، یعنی اسے نقل مکانی کرنٹ کے طور پر بیان کیا گیا ہے۔

اگر یہ سمجھا جائے کہ یہ حصہ کرنٹ کا وہ حصہ ہے جو پہلے دریافت نہیں ہوا تو اب مکمل کرنٹ ہے۔ کہنے کا مطلب یہ ہے کہ، اگرچہ پلیٹوں کے درمیان سرکٹ منقطع ہے، برقی نقل مکانی کے بہاؤ کا اخذ اور کرنٹ کا مجموعہ، مجموعی طور پر، ہر وقت کرنٹ کے تسلسل کو یقینی بنائیں۔

پچھلے تضاد کی طرف واپس جاتے ہوئے، اب ہم جانتے ہیں کہ سٹوکس کے تھیوریم کے تقاضوں کے مطابق، بند سطح کے لیے کرنٹ کی کثافت کے بہاؤ کا حساب لگاتے وقت، نقل مکانی کرنٹ کی کثافت پر بھی غور کیا جانا چاہیے، یعنی مکمل ایمپیئر لوپ۔ تھیوریم اس لیے ہے، اس نئے موجودہ جزو کو “دریافت” کرنے سے، ایمپیئر لوپ تھیوریم کا بحران حل ہو جاتا ہے!

وجہ یہ ہے کہ یہاں “تعارف” استعمال نہیں کیا گیا ہے، لیکن یہاں “دریافت” استعمال ہوا ہے۔ میں جس چیز پر زور دینا چاہتا ہوں وہ یہ ہے کہ اس قسم کا کرنٹ کوئی ریاضیاتی معاوضہ نہیں ہے، بلکہ ایک حقیقی چیز ہے، لیکن اس سے پہلے اسے دریافت نہیں کیا گیا تھا۔

یہ پہلی جگہ کیوں موجود ہے؟ چونکہ یہ برقی رو کے طور پر کام کرتا ہے، ایک ترسیلی کرنٹ کی طرح، یہ مقناطیسی میدان کو مساوی طور پر اکساتی ہے، سوائے اس کے کہ برقی چارجز کی کوئی حرکت نہیں ہوتی، کسی تار کی ضرورت نہیں ہوتی، اور کوئی جول حرارت پیدا نہیں کیا جا سکتا، اس لیے اسے نظر انداز کر دیا گیا ہے!

لیکن یہ اصل میں خود ہی موجود ہے، صرف ایک کم پروفائل رکھیں، یہ خاموشی سے وہاں موجود مقناطیسی میدان کو ہر وقت پرجوش کر رہا ہے!

دوسرے الفاظ میں، جب ہم مقناطیسی میدان کا سامنا کرتے ہیں، تو کرنٹ کی اصل تعریف بہت تنگ ہوتی ہے۔ برقی کرنٹ کا جوہر برقی چارج کی حرکت نہیں ہے، یہ ایسی چیز ہونی چاہیے جو مقناطیسی میدان کو متحرک کر سکے۔

اب تک، کرنٹ کی کئی شکلیں متعارف کرائی جا چکی ہیں۔ یہ سب معروضی طور پر موجود ہیں، اور ان میں جو چیز مشترک ہے وہ یہ ہے کہ تمام دھارے مقناطیسی میدان کو یکساں طور پر پرجوش کر سکتے ہیں۔